1.2. Понятия переносной угловой скорости и углового ускорения

Определение 4

Переносной мгновенной угловой скоростью  и переносным мгновенным угловым ускорением  называются мгновенная угловая скорость и мгновенное угловое ускорение подвижной системы координат относительно абсолютного пространства.

Из определения 4 и определения вектора мгновенной угловой скорости подвижной системы координат (см. гл.3, §8) следует

. (4.2.5)

Вектор является решением уравнений Эйлера

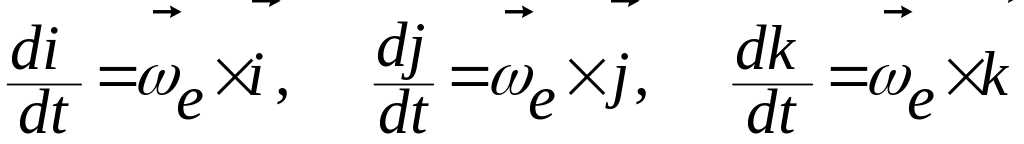, (4.2.6)

в которых вектора ,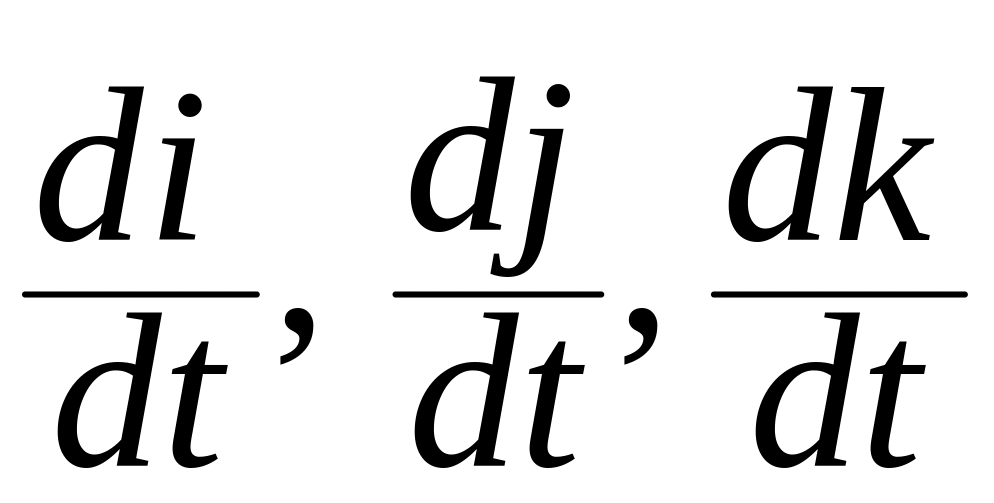 вычисляются на заданном движении базиса системы в фиксированный момент времени .

Вектор мгновенного углового ускорения переносного движения связан с зависимостью

. (4.2.7)

1.3. Формулы переносной скорости и переносного ускорения

Выведем формулы для переносной скорости  и переносного ускорения точки  .

1.3.1. Формула переносной скорости

В соответствии с определением 3 переносная скорость точки  в момент времени  совпадает с абсолютной скоростью той точки  фиктивного твердого тела, которая в этот момент совпадает по своему положению с точкой  .

Абсолютная скорость любой точки твердого тела задается формулой Эйлера

.

Здесь:

— положение точки в системе  ;

— абсолютная скорость полюса ;

— вектор мгновенной угловой скорости фиктивного твердого тела.

По определению фиктивного твердого тела система является для него связанной системой координат. Поэтому вектор угловой скорости фиктивного твердого тела совпадает с вектором угловой скорости системы .

Но вектор угловой скорости системы , согласно определению 4, является вектором переносной мгновенной угловой скорости .

Следовательно,

.

Кроме того, согласно определению 3, положение  точки  совпадает в момент времени  с положением точки , которое, в свою очередь, на относительном движении совпадает с .

Поэтому, подставляя и в выражение для скорости и учитывая, что согласно определению 3 переносная скорость  точки  совпадает со скоростью  точки  :

,

окончательно находим

. (4.2.8)

1.3.2. Формула переносного ускорения

Действуя аналогично, по определению 3 получим выражение для переносного ускорения точки , используя формулу Ривальса для ускорения точек твердого тела

. (4.2.9)

Здесь:

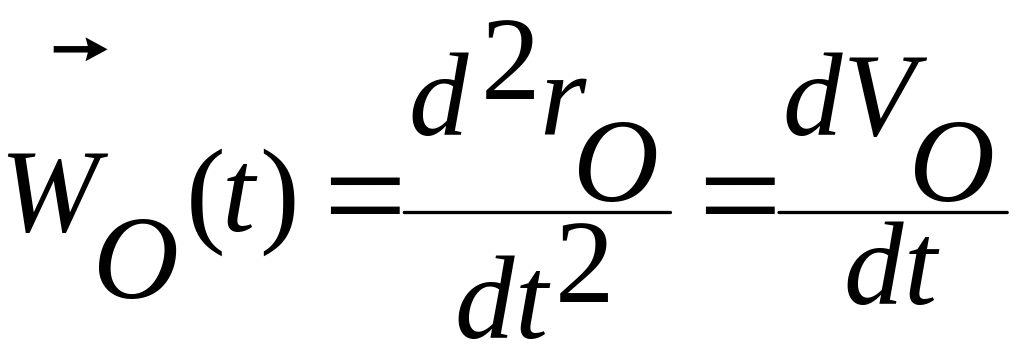• — абсолютное ускорение точки ;

• — вектор мгновенной угловой скорости переносного движения;

• — вектор мгновенного углового ускорения подвижной системы координат , определяемый по вектору  по формуле (4.2.7);

• — радиус-вектор точки  в момент времени  относительно полюса  подвижной системы, заданный проекциями на подвижные оси.

2º. Дифференцирование вектора, заданного в проекциях на подвижные оси

Выведем формулу для дифференцирования любого вектора, заданного своими проекциями на подвижные оси.

Итак, пусть вектор задается в проекциях на подвижные оси:

,

где

— орты подвижной системы координат,

— координаты вектора в этой системе

координат.

Дифференцируя по  обе части равенства, получим

. (4.2.10)

По определению относительной производной можем записать

.

Согласно формулам (4.2.6) Эйлера

, (4.2.6)

будем иметь

.

Поэтому, подставляя в правую часть равенства (4.2.10) полученные выражения для сумм векторов, окончательно находим:

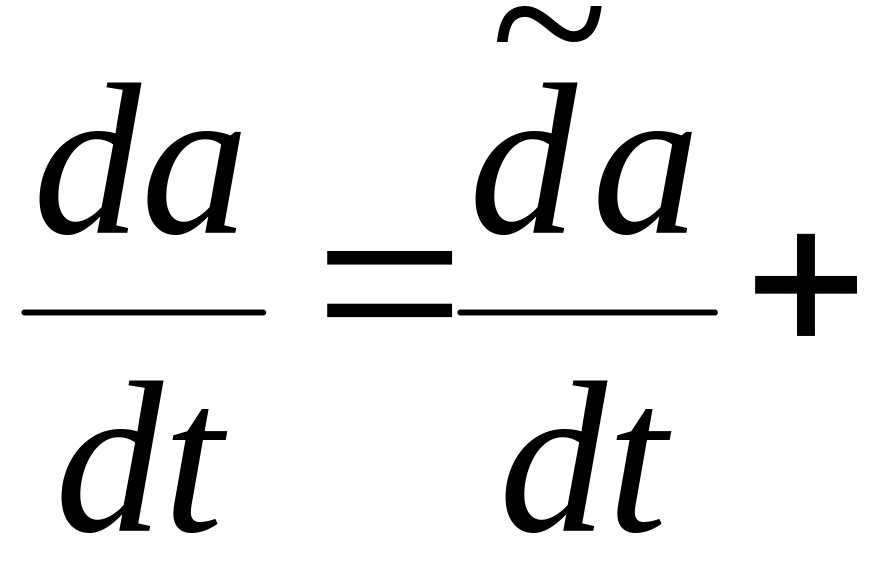
. (4.2.11)

Формула (4.2.11) устанавливает правило дифференцирования по времени любого вектора, заданного в проекциях на подвижные оси.