46

ЛЕКЦИЯ 7.Кинем-ка Гл.2 (Лекц.2 по гл.2) §3н.С. 1-25. Доп.1-5:с. 26-34, 35-38, 39-42, 43-47, 48-51. 31.07.2012

Глава 2. Кинематика системы материальных точек

§3. Линейные дифференциальные связи первого порядка и условия их интегрируемости

1º. Линейные дифференциальные связи первого порядка и их приведение к дифференциальным уравнениям в полных дифференциалах

1.1.Понятие линейных дифференциальных связей

Определение 1

Уравнения связей вида

, , (2.3.1)

называются линейными дифференциальными связями.

Здесь векторы и скалярные функции ,  , зависящие от векторов , и времени , являются непрерывно дифференцируемыми функциями компонент ,  , и времени .

В скалярной форме уравнения линейных дифференциальных связей записываются так:

, . (2.3.2)

Перейдем к матричной записи этих уравнений.

Введем обозначения:

, , ,…, , , ,

;

 — вектор-столбец размерности ;

— вектор-столбец размерности ;

; (2.3.3)

— матрица размерности , составленная из коэффициентов при уравнений (2.3.2):

, . (2.3.2)

Тогда система (2.3.2) примет вид:

. (2.3.2')

На матрицу (2.3.3) накладываем следующие условия:

1. матрица и вектор непрерывно дифференцируемы по компонентам вектора и по времени ;

2. , т.е. строки матрицы линейно независимы при любых .

1.2.Приведение к системе уравнений в полных дифференциалах

Умножим на каждое уравнение системы (2.3.2'):

. (2.3.2')

Получим систему

. (2.3.2'')

Учтем, что на движениях механической системы

,

и введем обозначения:

, , ;

при , при ;

.

Здесь:

— элемент матрицы  под номером ,

— элемент вектора  ;

— номер уравнения в системе (2.3.2'); принимает значения .

Присоединим к матрице  столбец  . Новую матрицу обозначим  .

Тогда в скалярной форме система уравнений (2.3.2''):

(2.3.2'')

примет вид

, . (2.3.4)

Здесь:

— дифференциал функции ;

— функции, непрерывно дифференцируемые по всем аргументам.

На уравнения (2.3.4) можно смотреть как на уравнения в полных дифференциалах (или точных дифференциалах), которые должны выполняться при любых значениях вдоль движений механической системы, удовлетворяющих уравнениям связей.

2º.Понятие уравнений в полных дифференциалах

В общем случае под системой уравнений в полных дифференциалах понимается следующая система уравнений

, , .

В ней:

• коэффициенты – функции, заданные и непрерывно дифференцируемые по совокупности аргументов при всех значениях ;

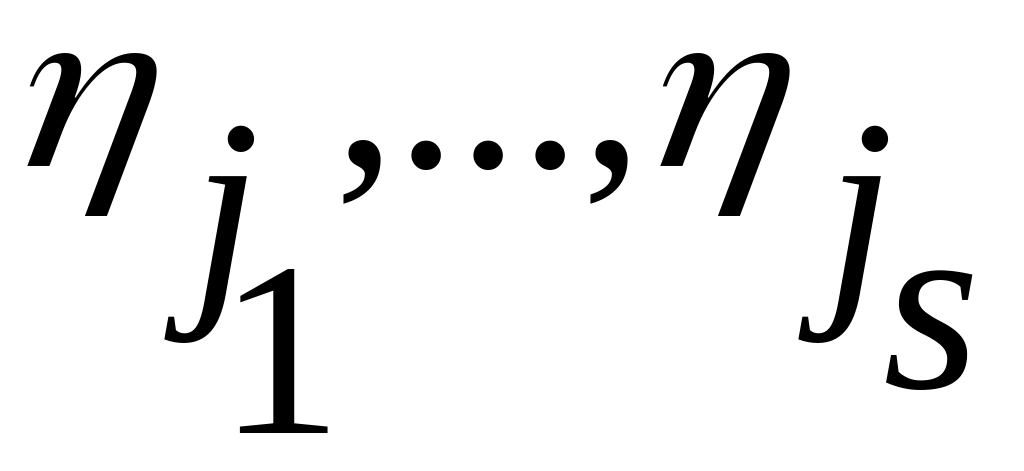• переменных среди аргументов – являются функциями, зависящими от остальных переменных ,  ,  ;

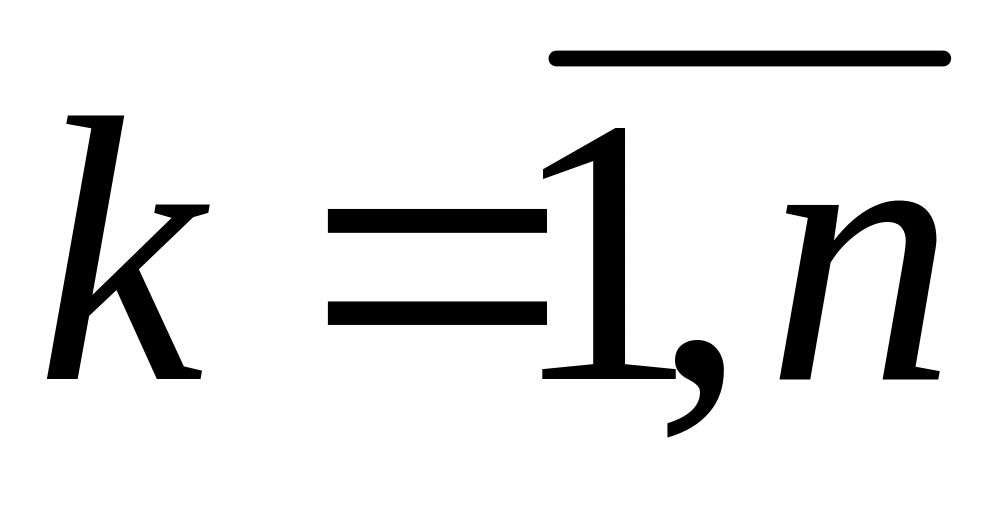• функции – предполагаются непрерывно дифференцируемыми по своим аргументам;

• – дифференциал функции ,  ;

• – дифференциал переменной  ,

,  ;

• если обозначим матрицу коэффициентов ,  , , то для нее выполняется условие:

при любых значениях .

Такая система уравнений называется системой уравнений в полных дифференциалах.