7. Испытание гипотезы для оценки линейности связи

Между переменными x, y предполагается наличие линейной связи y = α + βx + ε, где ошибка ε — это отклонение значения y от линии y = α + βx. Мы производим парную выборку значений переменных x, y и методом наименьших квадратов получаем оценки коэффици­ентов α и β – a и b соответственно. Очевидно, что для другой выбор­ки оценки a и b будут другими. Как, зная оценки a и b, убедиться, что Связь между переменными x, y действительно линейная?

7.1. Испытание гипотезы для оценки линейности связи на основе оценки коэффициента корреляции в генеральной совокупности

Показатель наличия линейной связи в генеральной совокупнос­ти – это коэффициент корреляции. Для генеральной совокупности он равен ρ. Нам это значение неизвестно. По данным выборки мы Получаем оценку для ρ – выборочный коэффициент корреляции r – и на основании r проводим испытание гипотезы о наличии линей­ной связи между переменными x, y в генеральной совокупности. Наш вывод о наличии линейной связи между переменными x, y генеральной совокупности зависит от объема выборки. Чем больше чем нашей выборки, тем надежнее полученный результат.

H₀: ρ = 0, то есть между переменными x, у отсутствует линейная связь в генеральной совокупности.

H₁: ρ ≠ 0, то есть между переменными x, у есть линейная связь в генеральной совокупности.

Задается доверительная вероятность p. Пусть n — объем парной выборки. Двусторонняя проверка, α = (1 – p)/2.

По таблице t-распределения находим t_{α; n-2}. В Excel для двусторон­ней проверки t_{α; n-2} = СТЬЮДРАСПОБР (1 – p; n – 2), для односто­ронней проверки t_{α; n-2} = СТЬЮДРАСПОБР (2×(1 – р); n – 2).

Граничные точки t_{α; n-2}.

Статистика t = √r²(n – 2)/(1 – r²).

Пример 4. Вернемся к примерам 1, 2. Проверим гипотезу о наличии линейной связи между переменными x, y в генеральной со­вокупности. Доверительная вероятность p = 95%. n = 5.

H₀: ρ = 0, то есть между переменными x, у отсутствует линейная связь в генеральной совокупности.

H₁: ρ ≠ 0, то есть между переменными x, у есть линейная связь в ге­неральной совокупности.

Проведем двустороннюю проверку.

α = (1 – p)/2 (1 – 0,95)/2 = 0,025.

По таблице t-распределения находим t_{α; n-2} = t_{0,025; 5-2} = 3,182. Граничные точки ±3,182.

Статистика t = √r²(n – 2)/(1 – r²) = √0,817× (5 – 2)/(1 – 0,817) ≈ 3,660.

Отметим значения на числовой оси.

H0 H1 2 ,5%	H0 9 5%	H0 H1 2 ,5%
-3,182	3,182	3,660

Мы отклоняем гипотезу H₀ и принимаем гипотезу H₁ на уровне значимости 5%. Между переменными x, y есть линейная связь в гене­ральной совокупности.

7.2. Испытание гипотезы для оценки линейности связи на основе показателя наклона линейной регрессии

В случае парной линейной регрессии функция показателя накло­на β аналогична функции коэффициента корреляции. Поэтому нуж­но ограничиться только одной проверкой.

H₀: β = 0, то есть между переменными x, y отсутствует линейная связь в генеральной совокупности.

H₁: β ≠ 0, то есть между переменными x, y есть линейная связь в генеральной совокупности.

Задается доверительная вероятность p. п — объем парной выбор­ки. Проведем двустороннюю проверку. В этом случае а = (1 — р)/2. По таблице t-распределения находим t_{α; n-2}. Граничные точки ± t_{α; n-2} .

Дисперсия распределения остатков вдоль линии регрессии 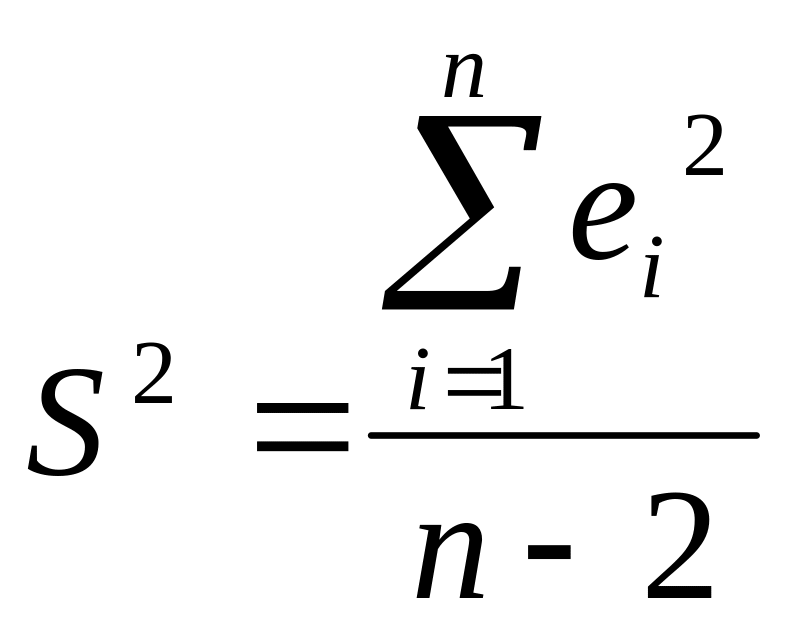, S – стандартная ошибка.

Стандартная ошибка коэффициента b:

Статистика t = b/S_b.

Пример 5. Вернемся к примерам 1, 2. Проверим гипотезу о наличии линейной связи между переменными x, у в генеральной со­вокупности. Доверительная вероятность p = 95%. n = 5.

H₀: β = 0, то есть между переменными x, y отсутствует линейная связь в генеральной совокупности.

H₁: β ≠ 0, то есть между переменными x, y есть линейная связь в генеральной совокупности.

Проведем двустороннюю проверку.

α = (1 – р)/2 = (1 – 0,95)/2 = 0,025.

По таблице t-распределения находим t_{α; n-2} = t_{0,025; 5-2} = 3,182. Граничные точки ±3,182.

Номер	ei	ei2
1	0	0
2	-0,09	0,0081
3	0,12	0,0144
4	0,03	0,0009
5	-0,06	0,0036
Сумма		0,0270

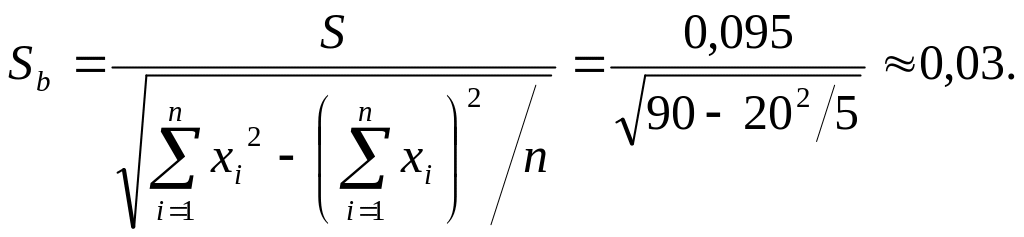
Статистика t = b/S_b = -0,11/0,03 ≈ 3,667.

Отметим значения на числовой оси.

H0 H1 2 ,5%	H0 9 5%	H0 H1 2,5%
-3,667	-3,182	3,182

Мы отклоняем гипотезу H₀ и принимаем гипотезу H₁ на уровне значимости 5%. Между переменными x, y есть линейная связь в гене­ральной совокупности.

Замечание. Для расчета стандартной ошибки вместо формулы 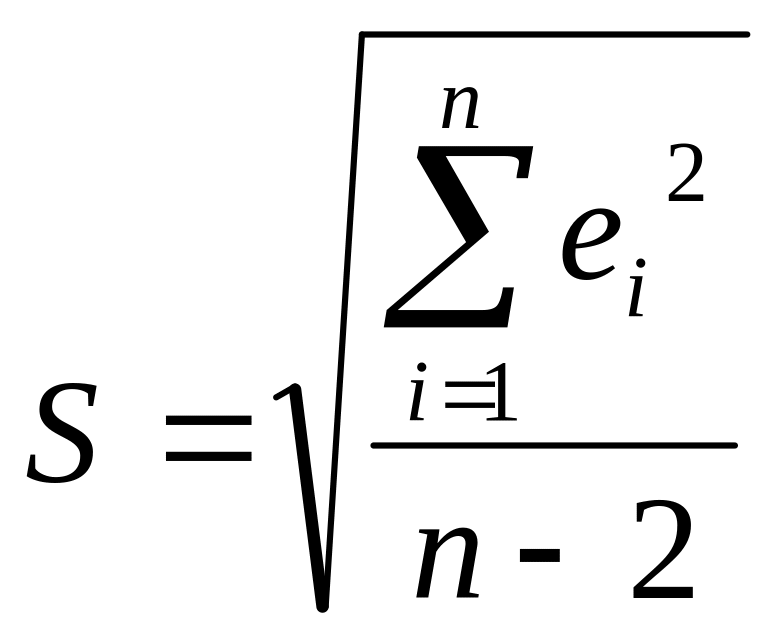можно воспользоваться статистической функцией СТОШУХ (изв_знач_y; изв_знач_x) мастера функций f_x пакета Excel.