3. Коэффициент корреляции пирсона. Коэффициент детерминации

Мы хотим знать, насколько хорошо приближает наши данные ли­нейная модель.

Формула y = a + bx только частично объясняет вариацию значе­ний y (а именно, слагаемое Но ведь на y влияют и другие фак­торы. Их влияние скрыто в остатке е_i. Если бы связь была строго линейной, то е_i = 0. И так для каждой точки x_i.

– это общая вариация переменной у.

– это вариация переменной у, которая объясняется формулой y = a + bx.

– это вариация переменной у, которая не объясняется формулой y = a + bx.

Введем характеристику 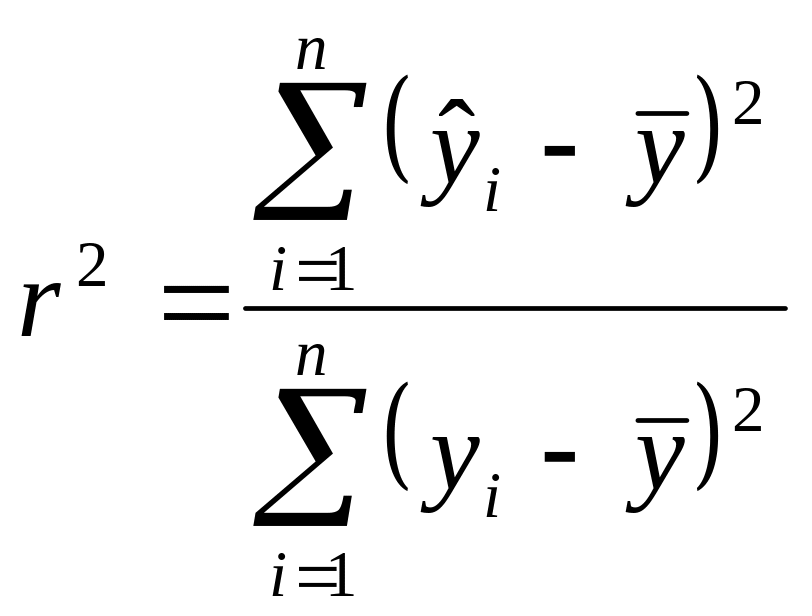- коэффициент детерминации. Эта мера показывает величину вариации переменной y, кото­рая объясняется переменной x при наличии линейной связи этих ве­личин. В случае строгой линейной зависимости между x и у r² = 1. Если зависимость между x и y отсутствует, то r² = 0.

Коэффициент детерминации не указывает причины и следствия. Он просто является математическим выражением взаимосвязи меж­ду переменными и показывает степень их взаимосвязанных измене­ний, хотя в экономической теории и можно постулировать причин­но-следственную связь между этими переменными.

Коэффициент корреляции Пирсона:

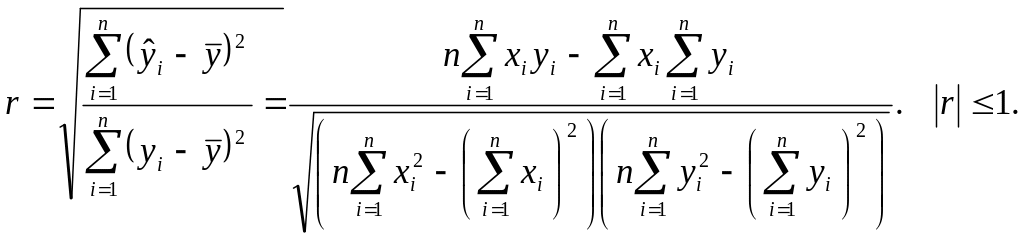
Вторая дробь – удобная расчетная формула, которую чаще всего используют.

Коэффициент корреляции Пирсона r содержит информацию о поведении y с ростом x. Знак коэффициента корреляции Пирсона r совпадает со знаком коэффициента b. Чем ближе r к 1, тем ближе связь между x и y к линейной. При r = 0 линейной связи между x и y не существует (но, возможно, между x и y есть другая зависимость).

Сильная корреляция между переменными необязательно указы­вает на причину и следствие. Например, может быть установлена сильная корреляция между зарплатой учителя и продажей спиртных напитков. Отсюда никак нельзя сделать вывод, что учителя пьют. Просто обе эти величины связаны через другую переменную – общий уровень наличного дохода. Это пример ложной корреляции.

Пример 2. Найдем остатки e_i, коэффициент корреляции Пир­сона и коэффициент детерминации в примере 1.

y = 2,12 – 0,11x. Заполним таблицу.

Номер	x	y	y2	ỹ =2,12 – 0,11x	е = у – ỹ
1	2	1,9	3,61	1,90	0,00
2	3	1,7	2,89	1,79	-0,09
3	4	1,8	3,24	1,68	0,12
4	5	1,6	2,56	1,57	0,03
5	6	1,4	1,96	1,46	-0,06
Сумма	20	8,4	14,26

Поясним, как заполняется таблица. В 4-м столбце указаны квад­раты соответствующих чисел 3-го столбца. Каждое число 2-го столб­ца подставляем в выражение 2,12 – 0,11x: и результат пишем в 5-м столбце. В 6-м столбце указана разность чисел 3-го и 5-го столбцов. В последней строке указана сумма чисел соответствующего столбца.

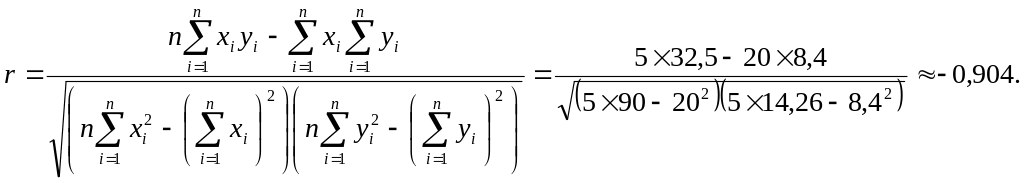
Это значение близко k–1, что свидетельствует об очень сильной отрицательной связи (с ростом х значения у убывают). Знаки b = –0,11 и r = –0,904 совпадают.

Коэффициент детерминации r² = (–0,904)² ≈ 0,817, то есть 81,7% общей вариации себестоимости y зависит от выпуска продукции х.

Наша модель не объясняет 18,3% вариации себестоимости. Эта часть вариации объясняется факторами, не включенными в модель.

Замечание. Для вычисления коэффициента корреляции Пирсона можно воспользоваться статистическими функциями ПИРСОН (массив 1; массив 2) или КОРРЕЛ (массив 1; массив 2) мастера функций f_x пакета Excel. Массив 1 и массив 2 – это ссылки на ячей­ки, содержащие значения переменных. Для вычисления коэффици­ента детерминации можно воспользоваться статистической функци­ей КВПИРСОН (изв_знач_y; изв_знач_x).