Задача оптимизации перевозок Постановка задачи
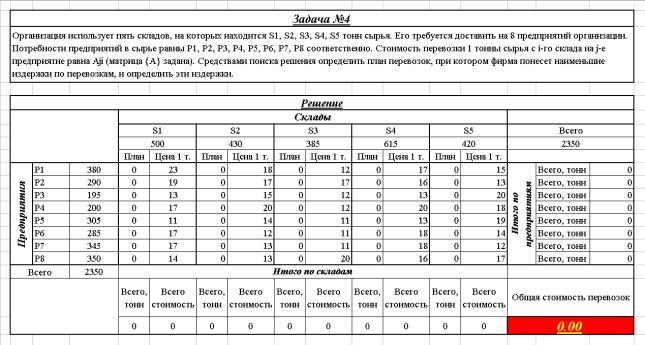
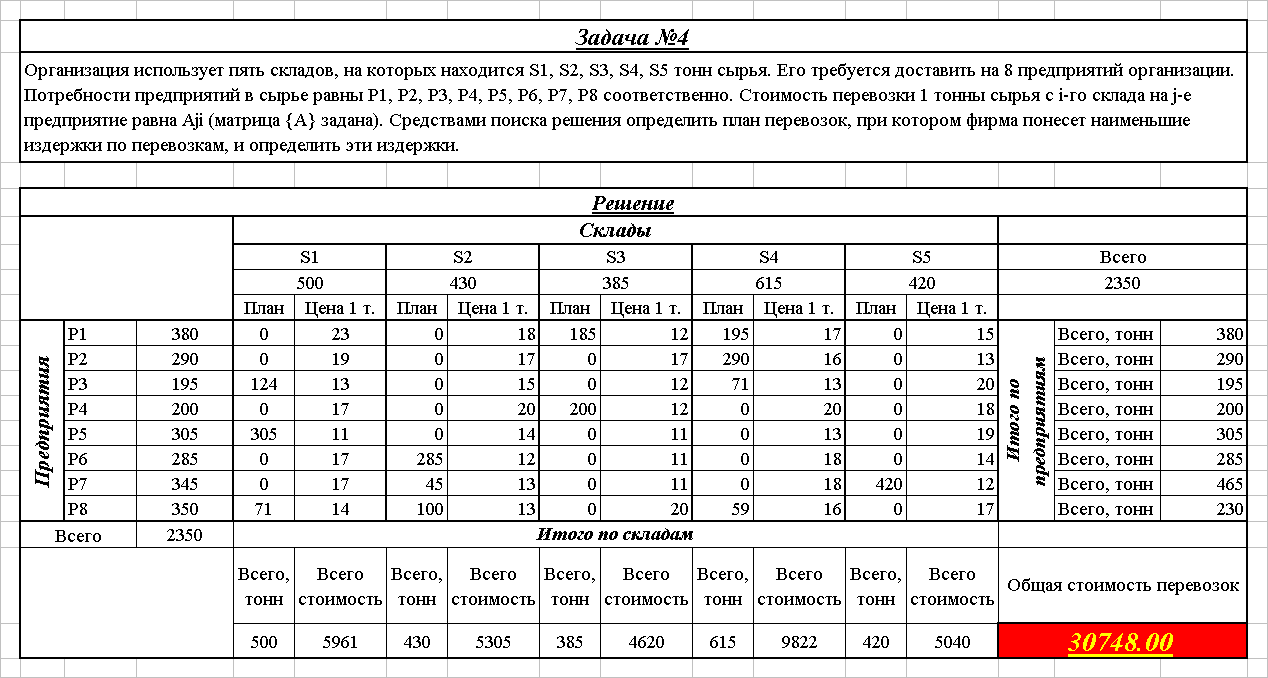
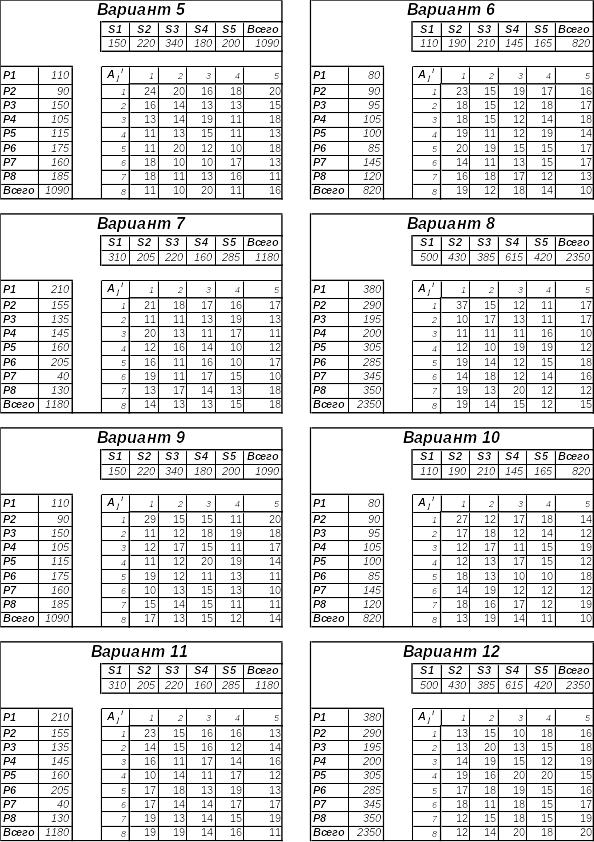
Организация использует пять складов, на которых находится S1, S2, S3, S4, S5 тонн сырья. Его требуется доставить на 8 предприятий организации. Потребности предприятий в сырье равны P1, P2, P3, P4, P5, P6, P7, P8 соответственно, причем Si = Pj. Стоимость перевозки 1 тонны сырья с i-го склада на j-е предприятие равна Aji (матрица {A} задана). Средствами поиска решения определить план перевозок, при котором фирма понесет наименьшие издержки по перевозкам, и определить эти издержки.
Номер варианта выбирается по сумме последних трех цифр зачетной книжки из таблицы
Варианты заданий
Рекомендации по математической модели и решению
Создать на листе математическую модель (см. ниже), задав в ней произвольные начальные значения (например, нули).
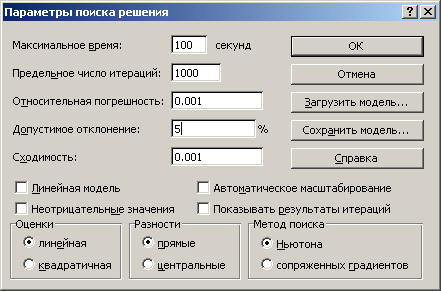
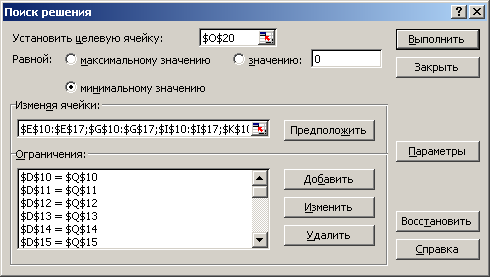
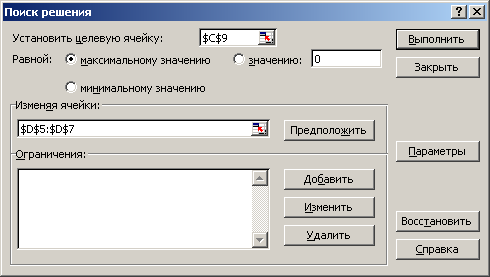
Вызвать средство поиска решения (меню Сервис) и установить параметры (рис. 1) и все требуемые ограничения (рис. 2).
|
рис. 1. Параметры поиска решения |
|
рис. 2. Ограничения поиска решения |
При выборе параметров рекомендуется использовать относительную погрешность 0,001 и допустимое отклонение 3-5%.
Изменяемые ячейки – план перевозок. Ограничения устанавливаются по смыслу задачи:
весь товар должен быть вывезен со складов, и все предприятия должны полностью удовлетворить свою потребность;
планируемые перевозки должны быть неотрицательны.
Найденное решение следует округлить до центнеров (1 знак после запятой) средствами форматирования ячеек.
|
рис. 3. Пример математической модели |
|
рис. 4. Пример оформления решения задачи |
Задача оптимизации плана выпуска продукции Постановка задачи
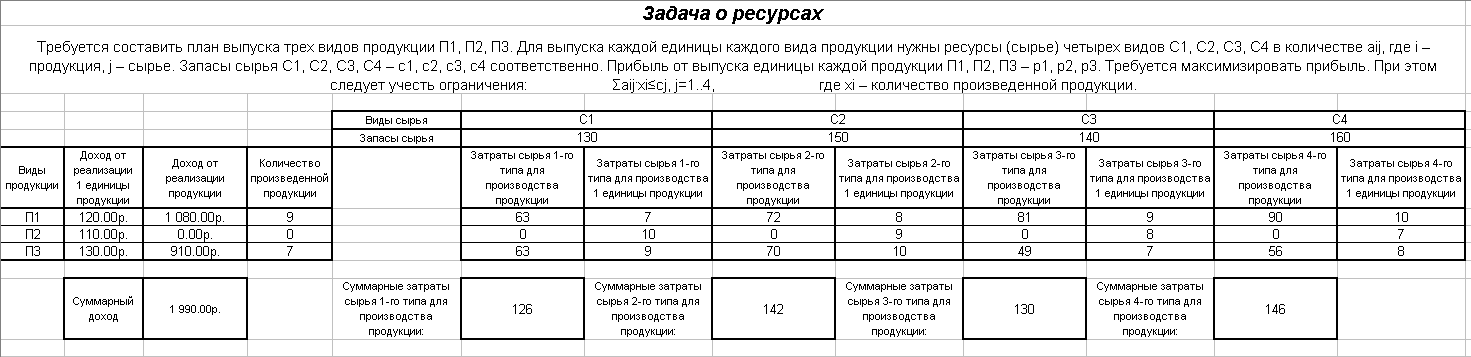
Требуется составить план выпуска трех видов продукции П1, П2, П3. Для выпуска каждой единицы каждого вида продукции нужны ресурсы (сырье) четырех видов С1, С2, С3, С4 в количестве aij, где i – продукция, j – сырье. Запасы сырья C1, C2, C3, C4 – c1, c2, c3, c4 соответственно. Прибыль от выпуска единицы каждой продукции П1, П2, П3 – р1, р2, р3. Требуется максимизировать прибыль. При этом следует учесть ограничения:
Σaij·xi≤cj, j=1..4,
где xi – количество произведенной продукции.
Варианты заданий
Номер варианта выбирается по сумме последних двух цифр зачетной книжки из таблицы
Варианты заданий приведены ниже в таблице
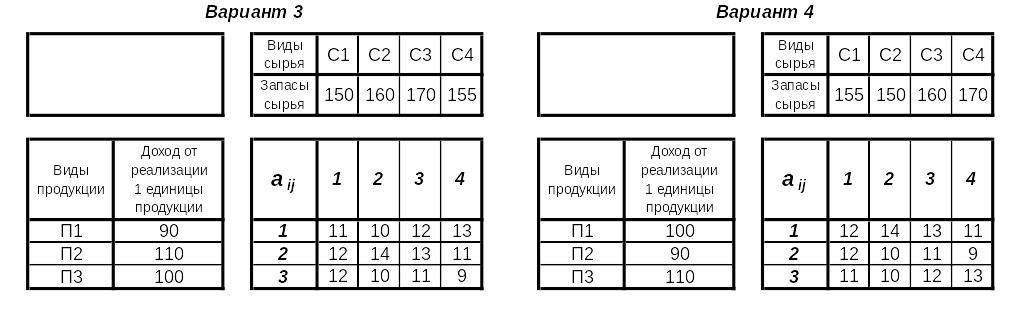
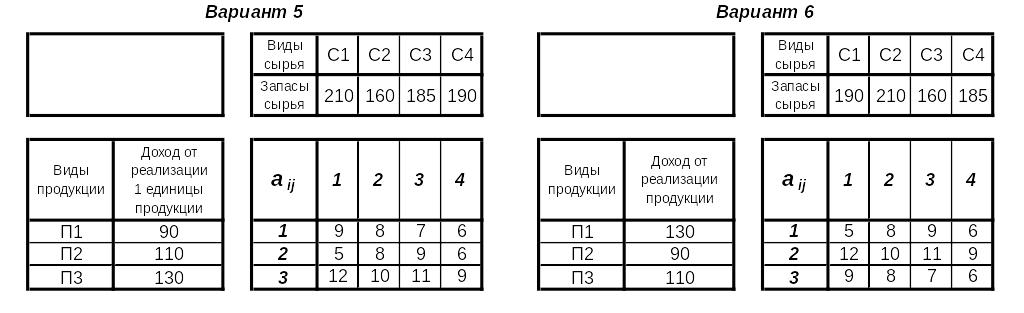
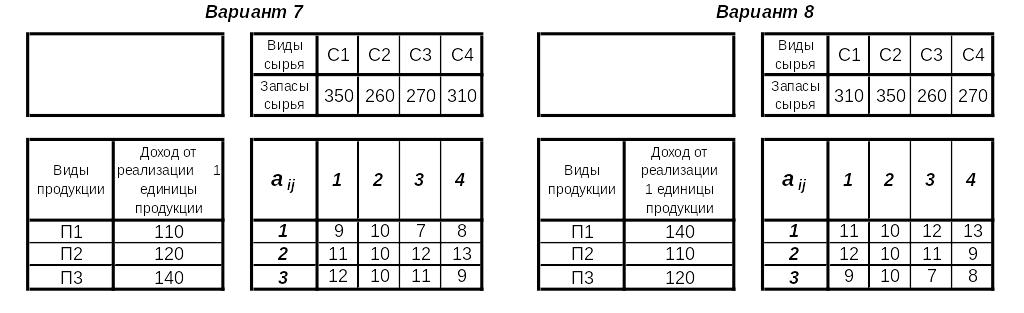
Рекомендации по математической модели и решению
Создать на листе математическую модель, задав в ней произвольные начальные значения (например, нули).
Вызвать средство поиска решения (меню Сервис) и установить параметры (рис. 5) и все требуемые ограничения (рис. 6).
|
рис. 5. Параметры поиска решения |
|
рис. 6. Ограничения поиска решения |
При выборе параметров рекомендуется использовать относительную погрешность 0,001 и допустимое отклонение 3-5%.
Изменяемые ячейки – Количество произведенной продукции. Ограничения устанавливаются по смыслу задачи:
расходы сырья при производстве не должны быть больше запасов сырья;
планируемые перевозки должны быть неотрицательны;
количество производимой продукции должно быть целым.
|
рис. 7. Пример математической модели |
