9. Задача выбора проекта (модели распределения капвложений).

Задача выбора проекта состоит из нескольких этапов. Схематически эти этапы можно представить следующим образом:

Формирование идеи → оценка идеи → выбор портфеля проектов → планирование работ → управление проектом → окончание

Формирование идеи определяется внешними условиями предприятия, оно зависит от спроса, конъектуры, технологических процессов и т.д. после того как будут намечены альтернативные варианты этих задач, осуществляется оценка выбранных альтернатив. Рассматривается применение мат.моделей в формировании портфеля инвестиционных проектов. Эти модели позволяют в комплексе определить:

• Размещение, размеры и специализацию производственных объектов

• Технологию производства

• Экономическую целесообразность реконструкций или дальнейшей эксплуатации производст. объекта

• Экономическую эффективность выбранных вариантов

• Распределение капитальных вложений во времени и по объектам

• И т.д.

Организац. задача развития производства классифицируется по ряду признаков:

• Критерий оптимальности

• Способу описания реконструкций и строительства предприятия

• Способу учета динамики развития предприятия и т.д.

Классифицированная модель планирования капвложений имеет следующий вид:

1) ∑_I ∑_j c_ij x_ij → ext

2) ∑_I ∑_j p_ij qt*x_ij ≥ A_qt q=1,2….Q, t=1,2…T

3) ∑_I ∑_j k_ijt x_ij ≤ k_i (t)

4) ∑_j x_ij ≤ 1

5) x_ij € {0,1} i=1,n j=1,m

x_ij = 1 ……если для i-го объекта принять j-й вариант развития.

c_ij - финансовый результат от реализации j-го проекта.

p_ij qt – объём производства qt-й продукции в году t при i-ом варианте развития j-го проекта

A_qt – объем спроса на qt-ю продукции в году t

Условие (2) явл-ся требованием удовлетворения спроса на продукцию

k_ijt - объем капвложений в году t j-го варианта развития i-го объекта

k_i (t) – объем капвложение выделенный на развитие j-го проекта в году t

Неравенство (3) представляет собой ограничение по объемам капвложений.

Равенство (4) представляет условие выбора одного из множества вариантов развития

Условие (5) накладывается на переменные решения задач

10. Сетевое планирование и управление.

После принятия решения о выборе проекта необходимо решить задачу планирования реализации проекта.

Для этого были разработаны методы сетевого планирования. В основе сетевого метода лежит построение сетевой модели представляющей собой графическое изображение комплекса операций реализации проекта. При составлении проекта на отдельные работы в результате чего появляется перечень работ.

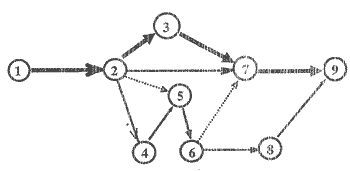
Дуги обозначают работы, а вершины – события.

Каждая работа характеризуется объемом ресурсов и продолжительностью работ.

Последовательность взаимосвязанных работ в сетевом графике образует путь µ. Продолжительность этого пути обозначается Т_µ . Путь идущий от начала сетевого графика до его конца и имеющий наибольшую продолжительность и называется критическим и обозначается µ_кр. Время Т_кр определяет срок выполнения всего комплекса работ.

Для анализа сетевого графика прежде всего необходимо определить время свершения событий. Следует различать возможные и допустимые сроки свершения работ.

Ai1Aj

Ai2Aj

Ai3Aj

Предположим, что имеется множество работ входящих в событие Ai1. Для того чтобы событие Aj свершилось необходимо закончить все работы AimAj. Тогда j-ое время Aj событие будет tb₃=≥max{t_pi+t_ij}

1. t_pi=≥max{t_pi+t_ij} - раннее время

Для того чтобы рассчитать раннее время свершения всех событий сетевого графика необходимо задать раннее время нулевой работы и потом по формуле (1) рассчитать время всех остальных событий слева направо. И последнее Тр9 = Ткр = время свершения всех работ.

Вторым параметром сетевого графика является допустимое время свершения событий и минимально допустимое определяет наиболее позднее время свершения работы.

t_qj ≤ min {t_ni – t_ji}

2. t_nj = min {t_ni – t_ji} – позднее время свершения всех событий сетевого графика

Для того чтобы рассчитать позднее время всех событий необходимо задать позднее время конечного события (t_n7). Далее двигаясь справа налево по формуле (2) рассчитывается позднее время каждого события.

Дальнейший анализ сетевого графика связан с понятием резерва времени. Различают: резерв времени пути, резерв времени работы и резерв времени события.

Rµ = Tкр - Tµ - резерв времени пути

Rj = tп_j - tр_j , j=1,n - резерв времени события

Rj = tп_j - tр_j – t_ij ; (Rjj = 0 для критического пути) – резерв времени работ

Таким образом критический путь занимает узкое место в комплексе работ.