Экспоненциальное сглаживание
Наиболее часто на практике применяются методы, используемые процедуру экспоненциального сглаживания.
Для экспоненциального сглаживания ряда используется следующая формула:
St =
St – значение экспонентной средней в момент времени t;
- параметр адаптации; 0≤
≤1
=1-
Если последовательно использовать данное соотношение, то экспоненциальную среднюю можно выразить через предшествующие значения уровней временных рядов:
St =
Таким образом, величина экспоненциальной средней оказывается взвешенной суммой всех уровней ряда, причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции.
Доказано, что дисперсия экспоненциальной средней меньше дисперсии временного ряда. Между этими дисперсиями существует следующее соотношение:
Дst=
При высоком значении параметра адаптации дисперсия экспоненциальной средней незначительно отличается от дисперсии временного ряда. С уменьшением , дисперсия экспоненциальной средней уменьшается, и возрастает ее отличие от дисперсии временного ряда. Тем самым экспоненциальная средняя начинает играть роль фильтра, поглощающего колебания временного ряда. Таким образом, с одной стороны следует увеличивать параметр адаптации, а с другой стороны, для сглаживания случайных отклонений, его следует уменьшать. Эти два требования находятся в противоречии. Поиск компромиссного значения параметра адаптации и составляет задачу оптимизации модели. Достаточно часто поиск значения параметра адаптации осуществляется путем перебора.
При использовании экспоненциальной средней для прогнозирования предполагается, что модель ряда имеет следующий вид:
Yt=a1,t+et
a1,t – варьирующий во времени средний уровень ряда;
et – случайное неавтокоррелированное отклонение от тренда.
Прогнозная модель определяется следующим соотношением:
у прогн = a1,t
a1,t – оценка a1,t
a1,t = St
Процедура прогнозирования временного ряда по методу экспоненциального сглаживания состоит из следующих этапов:
выбирается вид модели экспоненциального сглаживания, задается значение параметра адаптации;
определяются начальные условия.
Начальные условия обычно получают усреднением нескольких первых уровней ряда.
S0=
производится расчет значений соответствующих экспоненциальных средних;
находятся оценки коэффициента модели;
осуществляется прогноз на одну точку вперед, находятся отклонения фактического значения временного ряда от прогнозируемых. Этапы с 3 по 5 данной процедуры повторяются для всех t≤n;
окончательная прогнозная модель формируется на последнем шаге в момент t=n.
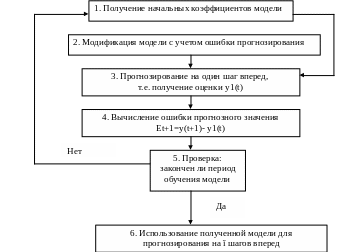
Рисунок - Схема построения адаптивных моделей прогнозирования
y(t) – фактические уровни временного ряда;
yǐ(t) – прогноз, сделанный в момент t на ǐ единиц времени (шагов) вперед;
Еt+1 – ошибка прогноза.