
- •Оценка погрешностей результатов измерений
- •Погрешности измерений и их типы
- •2. Оценка систематической (приборной) погрешности
- •3. Оценка случайной погрешности. Доверительный интервал и доверительная вероятность
- •4. Методика расчета погрешностей измерений. Погрешности прямых измерений
- •5. Погрешность косвенных измерений
- •6. Пример оформления лабораторной работы
- •Порядок выполнения работы
- •Результаты измерений
- •Оценка погрешностей измерения
- •2.Вычисление систематической (приборной) погрешности
- •4. Вычисление суммарной погрешности
- •5. Относительная погрешность, или точность измерений
- •6. Запись окончательного результата
- •6. Графическое представление результатов измерений
- •Общие рекомендации по построению графиков
РАСЧЕТ ПОГРЕШНОСТИ РЕЗУЛЬТАТОВ ПРЯМЫХ ИЗМЕРЕНИЙ
Для расчета погрешностей результатов прямых измерений некоторой величины х нужно [2] сделать несколько измерений этой величины. Обозначим число измерений и соответственно число результатов этих измерений буквой n. Напоминаем, что запись каждого из n результатов измерения должна обязательно содержать все цифры, в том числе и 0 вплоть до последнего разряда числа, соответствующего самому мелкому делению прибора. Далее обработка идет по следующей схеме.
1. Вычисляем среднее арифметическое значение величины х по формуле
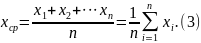
Среднее значение также должно содержать столько цифр, в том числе и нулей, сколько их в записях результатов измерений.
2. Вычисляем среднюю квадратичную погрешность величины х по формуле
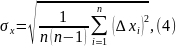
где ∆хi = хi – хср – абсолютная погрешность каждого из n результатов измерений. В записях квадратов этих абсолютных погрешностей должно содержаться в два раза больше цифр, в том числе и нулей, чем в записях результатов измерений. А в записи средней квадратичной погрешности – столько же цифр, что и в записях результатов измерений.
3. Вычисляем
предварительную абсолютную погрешность
измеряемой величины путем умножения
ее средней квадратичной погрешности
на коэффициент
Стьюдента
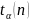 :
:
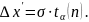 (5)
(5)
В записи этой погрешности должно содержаться столько же цифр, что и в записях результатов измерений. Значение коэффициента Стьюдента для данного числа n и для доверительной вероятности α = 95 % берем из таблицы, расположенной в следующем разделе.
4. Вычисляем окончательную абсолютную погрешность измеряемой величины с учетом погрешности прибора δ по формуле
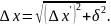 (6)
(6)
Значение этой погрешности нужно округлить, оставив только две значащие цифры.
5. Уточняем запись среднего значения измеряемой величины, сопоставив его с величиной абсолютной погрешности. Число, обозначающее среднее значение измеряемой величины, нужно округлить, оставив в нем все цифры вплоть до разряда, являющегося последним в окончательной записи абсолютной погрешности. Записываем результат измерений в виде суммы округленного среднего значения и абсолютной погрешности:
х = хср ± Δх. (7)
Например, мы получили следующие величины: среднее значение хср = 2,36752 и значение окончательной абсолютной погрешности: Δх = 0,08364. После округления получим Δх = 0,084. Следовательно, среднее значение нужно округлить до тысячных: хср = 2,368. Окончательно запишем
х = 2,368 ± 0,084.
6. Вычисляем относительную погрешность измеряемой величины по формуле
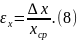
Относительную погрешность, как правило, выражают в процентах. Значение этой погрешности нужно округлить, оставив только две значащие цифры.
Отметим, что величина относительной погрешности определяется конкретными условиями проведения самого процесса измерения, но сама эта величина не известна. Описанный выше метод позволяет произвести оценку величины этой погрешности. Причем с ростом числа измерений результат оценки погрешности будет все ближе к истинному значению величины относительной погрешности. Однако увеличение числа измерений никогда не приведет к уменьшению самой погрешности.
КОЭФФИЦИЕНТ СТЬЮДЕНТА
Число прямых измерений всегда конечно. Поэтому средняя квадратичная погрешность заведомо меньше истинной абсолютной погрешности. Чтобы получить близкое к реальности значение абсолютной погрешности, нужно увеличить среднюю квадратичную погрешность, умножив ее на коэффициент Стьюдента . В теории Стьюдента рассчитаны значения этого коэффициента в зависимости от доверительной вероятности α и числа измерений n. С ростом доверительной вероятности, то есть надежности значения абсолютной погрешности, коэффициент Стьюдента увеличивается. А с ростом числа измерений, увеличивающим надежность самих результатов измерения, коэффициент Стьюдента уменьшается. Ниже приведены значения коэффициента Стьюдента для доверительной вероятности α = 0,95.
n |
2 |
3 |
4 |
5 |
6 |
tα (n) |
12,71 |
4,303 |
3,182 |
2,776 |
2,571 |
n |
7 |
8 |
9 |
10 |
20 |
tα (n) |
2,447 |
2,365 |
2,306 |
2,262 |
2,093 |
Отметим, что запись результата измерения в форме (7) означает, что значение измеренной величины x с заданной вероятностью α не выйдет за пределы интервала (xср – Δx, xср + Δx). Поэтому абсолютную погрешность Δx
часто называют полушириной доверительного интервала.
РАСЧЕТ ПОГРЕШНОСТИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ
Результат косвенного измерения есть результат расчета по заданной формуле. Оценка относительной погрешности результата расчета уже описана выше. Относительная погрешность рассчитывается по формуле (2), если величины, полученные в результаты прямых измерений, входят в заданную формулу в качестве множителей или делителей.
Для примера рассмотрим косвенное измерение объема прямого цилиндра высоты h с диаметром d. Объем такого цилиндра можно вычислить по формуле
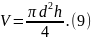
Для вычисления объема цилиндра по формуле (9) нужно иметь результаты измерения его диаметра и высоты. Пусть в результате прямых измерений получены значения диаметра и высоты цилиндра в соответствии с (7):
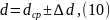
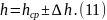
В этом случае известны и относительные погрешности значений диаметра и высоты цилиндра:
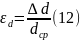
и
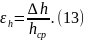
Прежде, чем приступать к вычислению объема, оценим относительную погрешность результата вычисления по формуле (9). В эту формулу входят четыре величины (числа). Два числа из них пришли из математики и являются, а скорее считаются, абсолютно точными: это числа 4 и π. Но число 4 – конечное число, а число π – является бесконечной непериодической дробью. Как это будет показано, можно взять округленное значение числа π с таким количеством значащих цифр, что это число практически не внесет никакой погрешности в окончательный результат расчета значения объема цилиндра.
Таким образом, источниками погрешности являются значения диаметра и высоты цилиндра. Обе эти величины входят множителями в формулу (9), но диаметр входит множителем два раза (в квадрате), а высота – один раз. Следовательно, подстановка этих величин в формулу (9) приведет к сложению двух относительных погрешностей диаметра и одной относительной погрешности высоты. Согласно формуле (2), относительная погрешность объема составит
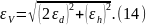
Как видим, наибольший вклад в относительную погрешность объема цилиндра вносит неточность измерения диаметра цилиндра. Поэтому для уменьшения погрешности результата необходимо именно диаметр цилиндра измерить с как можно большей точностью.
Чтобы число π не внесло дополнительную погрешность в результат вычисления объема, нужно взять его значение с относительной погрешностью, много меньшей погрешностей диаметра и высоты цилиндра. Поскольку, как нам известно, точность числа зависит от количества значащих цифр в нем, нужно взять столько цифр числа π, чтобы их количество на одну цифру превышало бы максимальное число значащих цифр в средних значениях диаметра и высоты. Вот запись округленного числа π, содержащая 7 значащих цифр: π = 3,141593.
Теперь, взяв число π с необходимым количеством значащих цифр, можно выполнить расчет среднего значения объема цилиндра по формуле (9):
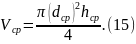
После этого нужно выполнить расчет относительной погрешности значения объема по формуле (14). Затем вычислить абсолютную погрешность объема по формуле
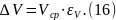
Значение этой погрешности нужно округлить, оставив только две значащие цифры. Затем нужно уточнить запись среднего значения объема, сопоставив его с величиной абсолютной погрешности (16). Число, обозначающее среднее значение объема, нужно округлить, оставив в нем все цифры вплоть до разряда, являющегося последним в окончательной записи абсолютной погрешности. Записываем результат измерений в виде суммы округленного среднего значения и абсолютной погрешности:
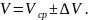
Например, мы
получили следующие величины: среднее
значение
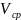 = 3867,395 мм3,
= 3867,395 мм3,
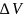 = 4,258 мм3.
Округляем значение
до двух значащих цифр, получаем
= 4,3 мм3.
Вторая значащая цифра находится в
разряде десятых долей миллиметра.
Значит, последней оставленной цифрой
в записи
должна быть цифра 3, стоящая в этом же
разряде. Первой отбрасываемой цифрой
является 9 ˃ 5, следовательно, нужно
добавить 1 к оставленной тройке. В итоге
получим: V
= (3867,4
= 4,258 мм3.
Округляем значение
до двух значащих цифр, получаем
= 4,3 мм3.
Вторая значащая цифра находится в
разряде десятых долей миллиметра.
Значит, последней оставленной цифрой
в записи
должна быть цифра 3, стоящая в этом же
разряде. Первой отбрасываемой цифрой
является 9 ˃ 5, следовательно, нужно
добавить 1 к оставленной тройке. В итоге
получим: V
= (3867,4
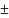 4,3) мм3
= (3,8674
0,0043)
4,3) мм3
= (3,8674
0,0043)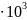 мм3
= (3,8674
0,0043)
мм3
= (3,8674
0,0043)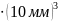 = (3,8674
0,0043)
= (3,8674
0,0043)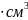 .
Окончательно:
.
Окончательно:
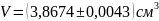
с относительной погрешностью, равной
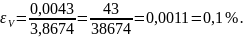
ЛИТЕРАТУРА
1. Метрология. Термины и определения. ГОСТ 16263–70. – М.: Изд-во стандартов, 1982. – 52 с.
2. Правила определения оценок и доверительных границ для параметров нормального распределения. ГОСТ 11004 – 74. – М.: Изд-во стандартов, 1981. – 20 с.
Оценка погрешностей результатов измерений
Погрешности измерений и их типы
Любые измерения всегда производятся с
какими-то погрешностями, связанными с
ограниченной точностью измерительных
приборов, неправильным выбором, и
погрешностью метода измерений, физиологией
экспериментатора, особенностями
измеряемых объектов, изменением условий
измерения и т.д. Поэтому в задачу измерения
входит нахождение не только самой
величины, но и погрешности измерения,
т.е. интервала, в котором вероятнее всего
находится истинное значение измеряемой
величины. Например, при измерении отрезка
времени t секундомером с
ценой деления 0,2 с можно сказать, что
истинное значение его находится в
интервале от
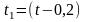 с
до
с
до
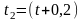 с.
Таким образом, измеряемая величина
всегда содержит в себе некоторую
погрешность
с.
Таким образом, измеряемая величина
всегда содержит в себе некоторую
погрешность
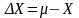 ,
где
,
где
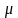 и X – соответственно
истинное и измеренное значения исследуемой
величины. Величина
и X – соответственно
истинное и измеренное значения исследуемой
величины. Величина
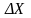 называется абсолютной погрешностью
(ошибкой) измерения, а выражение
называется абсолютной погрешностью
(ошибкой) измерения, а выражение
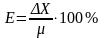 ,
характеризующее точность измерения,
называется относительной погрешностью.
,
характеризующее точность измерения,
называется относительной погрешностью.
Вполне естественно стремление экспериментатора произвести всякое измерение с наибольшей достижимой точностью, однако такой подход не всегда целесообразен. Чем точнее мы хотим измерить ту ил иную величину, тем сложнее приборы мы должны использовать, тем больше времени потребуют эти измерения. Поэтому точность окончательного результата должна соответствовать цели проводимого эксперимента. Теория погрешностей дает рекомендации, как следует вести измерения и как обрабатывать результаты, чтобы величина погрешности была минимальной.
Все возникающие при измерениях погрешности обычно разделяют на три типа – систематические, случайные и промахи, или грубые ошибки.
Систематические погрешности обусловлены ограниченной точностью изготовления приборов (приборные погрешности), недостатками выбранного метода измерений, неточностью расчетной формулы, неправильной установкой прибора и т.д. Таким образом, систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Величина этой погрешности систематически повторяется либо изменяется по определенному закону. Некоторые систематические ошибки могут быть исключены (на практике этого всегда легко добиться) путем изменения метода измерений, введение поправок к показаниям приборов, учета постоянного влияния внешних факторов.
Хотя систематическая (приборная) погрешность при повторных измерениях дает отклонение измеряемой величины от истинного значения в одну сторону, мы никогда не знаем в какую именно. Поэтому приборная погрешность записывается с двойным знаком
Случайные погрешности вызываются большим числом случайных причин (изменением температуры, давления, сотрясения здания и т.д.), действия которых на каждое измерение различно и не может быть заранее учтено. Случайные погрешности происходят также из-за несовершенства органов чувств экспериментатора. К случайным погрешностям относятся и погрешности обусловленные свойствами измеряемого объекта.
Исключить случайны погрешности отдельных измерений невозможно, но можно уменьшить влияние этих погрешностей на окончательный результат путем проведения многократных измерений. Если случайная погрешность окажется значительно меньше приборной (систематической), то нет смысла дальше уменьшать величину случайной погрешности за счет увеличения числа измерений. Если же случайная погрешность больше приборной, то число измерений следует увеличить, чтобы уменьшить значение случайной погрешности и сделать ее меньше или одного порядка с погрешностью прибора.
Промахи, или грубые ошибки, - это неправильные отсчеты по прибору, неправильная запись отсчета и т.п. Как правило, промахи, обусловленные указанными причинами хорошо заметны, так как соответствующие им отсчеты резко отличаются от других отсчетов. Промахи должны быть устранены путем контрольных измерений. Таким образом, ширину интервала в котором лежат истинные значения измеряемых величин, будут определять только случайные и систематические погрешности.
