8. Моделирование систем (сущность моделирования, классификация моделей, этапы моделирования). Сущность моделирования

. В данной лекции мы остановимся только на некоторых фундаментальных по­нятиях системного подхода, чтобы иметь возможность познако­миться со знаковой символикой, позволяющей формализовать по­нятия системы, образующих ее элементов и внешней (по отноше­нию к ней) среды.

Если элементы, образующие некоторую систему S , обозна­чить символами Х₁, Х₂, ..., Хn, где n — число элементов, то мно­жество

X = {Х₁,Х₂,.,.,Х_п}

состоящее из всех внутренних элементов, естественно назвать со­ставом системы S .

Элементы X₁, Х₂, ..., Х _nсвязаны между собой различными связями и отношениями, которые называются системообразующими, так как именно их наличие превращает набор элементов в целостную систему. Однако, кроме того, что эти элементы связаны между со­бой, они испытывают воздействие со стороны внешних относитель­но системы S объектов, а также, возможно, сами влияют на по­следние.

Рассуждая формально, каждая система S воздействует сама и испытывает воздействие со стороны бесчисленного множества внешних по отношению к ней систем S₁, S₂, ..., S_m, S_m+I, однако, избрав определенную меру интенсивности воздействия, можно установить конечное число внешних систем S₁, ..., S_m, находящихся с данной системой S во взаимодействии, с интенсивностью не менее некоторого заданного уровня. Множество, состоящее из всех внешних систем, находящихся в существенной (в указанном смысле) связи с данной системой S , назовем ее непосредственной окружающей средой системы S и обозначим

V = {S₁, S₂, ..., S_k}.

Множество связей (отношений) элементов системы между со­бой, а также элементов системы с внешней средой назовем струк­турой системы S и обозначим так: Σ=(σ_1, …, σ_r), где r — число всех рассматриваемых связей, образующих струк­туру системы S .

Внешняя среда, состав и структура системы могут изменяться с течением времени.

Функцией системы S назовем закон (совокупность правил) (F, по которому в зависимости от внешних факторов V(t) происходит изменение во времени внутренних элементов X (t) и струк­туры Σ (t) системы S .

Суммируя вышесказанное, можно дать следующее определение понятия системы:

Системой, функционирующей в окружающей среде, называется объект,

образованный элементами множества X, которые связаны между собой и с окружающей средой определен­ными связями (отношениями). Совокупность связей образует структуру Σ. И состав X (t), и структура Σ (t) изменяются во времени в соответствии с функцией F .

Системный подход к изучению любого объекта, например эко­системы, состоит, во-первых, в определении образующих ее со­ставных частей — Х₁, ..., Х_n и взаимодействующих с ней объектов окружающей среды — S₁ ..., S_k , во-вторых, в установлении струк­туры экосистемы, т. е. совокупности внутренних связей и отноше­ний σ₁, ..., σ_r, а также связей между экосистемой и окружающей средой и, в-третьих, в нахождении функции (закона функциони­рования) экосистемы F, определяющей характер изменения ком­понентов экосистемы и связей между ними под действием внеш­них объектов.

Сущность метода моделирования состоит в том, что на­ряду с системой (оригиналом), которую мы обозначим через

,

рассматривается ее модель, в качестве которой выступает некоторая другая система — , представляющая собой образ (подобие) ори­гинала S° при моделирующем отображении f (соответствии подо­бия), т. е. не все черты состава и структуры оригинала отражают­ся моделью.

Моделирующее отображение f целесообразно представить в виде композиции (продукта последовательного выполнения) двух отображений — огрубляющего g и гомоморфного h:¹

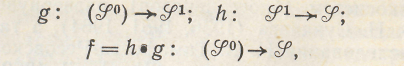где S¹ = S¹ (V¹, X¹, Σ¹, F¹) — некоторая подсистема системы S°, т. е. V¹ V⁰, X¹ X⁰ и Σ ¹ Σ⁰. Модель, как правило, представляет собой упрощенный образ оригинала, и это упроще­ние (огрубление) осуществляется отображением g, при котором, сознательно удаляя из системы S⁰ некоторые элементы и связи, мы получаем подсистему S¹. С другой стороны, мо­дель должна в определенном смысле верно отражать оригинал, хотя возможно и огрублено, или, как принято говорить в систем­ном анализе, агрегировано. Именно это и осуществляет гомо­морфное отображение подсистемы S ¹ на модель S⁰. При этом мо­жет произойти дальнейшее огрубление, т. е. число элементов и связей в модели S может стать меньше, чем в S ¹, а тем более в S°, однако при этом не происходит искажения структуры, т. е. если некоторые элементы системы S¹ были связаны некоторыми отношениями, то их образы в модели S должны быть связаны образом этого же отношения.

В зависимости от характера огрубления и степени агрегиро­вания для одного и того же оригинала можно получить несколь­ко различных моделей.

Стратегия моделирования заключается в попытке путем упро­щения получить модель, свойства и поведение которой можно бы­ло бы эффективно изучать, но которая в то же время оставалась бы достаточно сходной с оригиналом, чтобы результаты этого изу­чения все же были применимы и к оригиналу. Обычно оригинал S° представляет собой достаточно сложную систему, непосредственное установление закона функционирования которой F° сопряжено с большими трудностями. В то же время для некоторой ее модели S ввиду ее относительно большей про­стоты функция F может быть найдена тем или иным путем. По­сле этого исследование системы S° можно заменить исследова­ниями ее модели S , а затем интерпретировать полученные ре­зультаты применительно к системе-оригиналу. S°. Таким образом, при помощи моделирования в некотором приближении, определяе­мом степенью близости модели к оригиналу, может быть решена задача установления функции изучаемой сложной системы S°.

Оригинал и модель, а также разные модели одного и того же оригинала могут отличаться по своей реализации, где под реали­зацией понимается характеристика того, «из чего и как модель сделана». Одно из достоинств метода модели­рования состоит в возможности построения моделей с «удобной» реализацией, ибо удачный выбор реализации делает исследова­ние модели несравненно более легким, чем исследование ориги­нала, и в то же время позволяет сохранить существенные черты его состава, структуры и функционирования.