Приклад
Приклад1. Знайти суму позитивних елементів у масиві. Етапи рішення завдання:
Алгоритм рішення досить простий - у циклі будемо "пробігати" масив, порівнюючи його осередку з 0 і підсумувати, якщо вони >0.
Складемо блок-схему програми
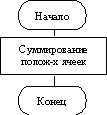
Уточнимо з яких блоків складається блок"Підсумовування позитивних осередків"
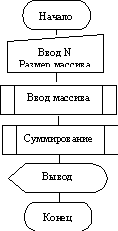
Зміст цих блоків простої, тому не коштує їх уточнювати.
Напишемо програму мовою Паскаль
program example;
type
Tarray = array[1..100] of integer;
Var v: Tarray;
N,i,s:integer;
Procedure vvod_data(var m:Tarray;n:integer);
Var i:integer;
Begin
Writeln('Уведіть ',n,' чисел через пробіл');
For i:= 1 to n do read(m[i]);
End;
Function summ(m:TArray):integer;
Vars:integer;
Begin
S:=0;
Fori:=1tondoifm[i]>0thens:=s+m[i];
Summ:=s;
End;
begin
write('Уведіть розмірність масиву N= '); readln(n);
vvod_Data(v,n);
s:= summ(v);
writeln('Сума= ',s);
end.
Завдання
Дано дійсні числа х1, в1, х2, в2, ...,х10, в10. Знайти периметр десятикутника, вершини якого мають відповідно координати (х1, в1), (х2, в2), ..., (х10, в10). (Визначити процедуру обчислення відстані між двома крапками, заданими своїми координатами.)
Дано дійсні числа a, b, c, d, e - сторони п'ятикутника. Знайти площу п'ятикутника. (Визначити процедуру обчислення площі трикутника по його сторонах.)
Дано три символьні матриці. a) ту матрицю, де є хоча б один гласна - транспонувати; b) у тій матриці, на головній діагоналі якої всі цифри, знайти найменшу й видалити відповідний рядок.
Написати програму обчислення P по формулі: де n - задане натуральне число.
Описати функцію Stepen (x,n) від речовинного x і цілого n, що обчислює (за допомогою множення) величину xn, і використовувати ee для обчислення b=2.7k+(a+1)-5.
Дано відрізки a,b,c і d. Для кожної трійки цих відрізків, з яких можна побудувати трикутник, надрукувати площа даного трикутника. Визначити процедуру Plo(x,y,z), що друкує площу трикутника зі сторонами x,y і z, якщо такий трикутник існує.
Нехай процедура Socr(a,b,p,q) від цілих параметрів (b№0)приводить дріб/ до нескоротного виду /Описати дану процедуру й використовувати неї для приведення дробу/ до нескоротного виду /
Дано довжини a,b і c сторін деякого трикутника. Знайти медіани трикутника, сторонами якого є медіани вихідного трикутника. Довжина медіани, проведеної до сторони a, дорівнює /
Дано координати вершин двох трикутників. Визначити, який з них має більшу площу.
Дано координати вершин трикутника й координати деякої крапки всередині нього. Знайти відстань від даної крапки до найближчої сторони трикутника. (При визначенні відстаней урахувати, що площа трикутника обчислюється й через три його сторони, і через підставу й висоту.). Завдання на кмітливість
Три прямі на площині задані рівняннями akx+bky=ck, k=1,2,3. Якщо ці прямі попарно перетинаються й утворять трикутник, тоді знайти його площу.
Два натуральних числа називаються "дружніми", якщо кожне з них дорівнює сумі всіх дільників іншого, за винятком його самого (такі, наприклад, числа 220 і 284). Надрукувати все пари "дружніх" чисел, що не перевершують заданого натурального числа.
Дано парне число n > 2. Перевірити для цього числа гіпотезу Гольдбаха. Ця гіпотеза (по сьогоднішній день не спростована й повністю не доведена) полягає в тім, що кожне парне n, більше двох, представляється у вигляді суми двох простих чисел. Скористатися функцією розпізнавання простих чисел.
Дано натуральне число n. З'ясувати, чи є воно повним квадратом. Визначити функцію, що дозволяє розпізнавати повні квадрати.
Дано масив A[1..50], елементи якого відмінні від нуля. Розташувати їх у такому порядку, щоб першими були всі позитивні елементи, а потім - всі негативні, причому порядок проходження як позитивних, так і негативних елементів повинен зберегтися (при рішенні завдання новий масив не заводити!).
Перетворити масив S, "повертаючи" його навколо центра на 90, 180, 270 градусів проти годинникової стрілки.
Розглядаючи масиви X, Y і Z як подання деяких безлічей з об'єктів типу індекс (X[k]=TRUE, якщо елемент k належить безлічі X, і X[k]=FALSE інакше, і т.п.), реалізувати наступну операцію над цими масивами-безлічами: змінної t привласнити значення TRUE, якщо безліч X є підмножиною безлічі Y, і значення FALSE інакше.
Елемент двомірного масиву називається локальним мінімумом, якщо він строго менше всіх наявних у нього сусідів. Підрахувати кількість локальних мінімумів заданої матриці розміром Nx знайти максимум серед всіх локальних мінімумів.
Скласти функцію для знаходження точного значення суми натуральних чисел, у десятковому записі яких більше 20 знаків. Вказівка. Вихідні дані й відповідь представити у вигляді масивів цифр.
Дано два рядки символів. Символ будемо називати загальним, якщо він зустрічається й у першої, і в другому рядку. Нехай K1 - число входжень у перший рядок загального символу, а K2 - у другу. Мінімальне із чисел K1, K2 будемо називати числом спільності. Вивести всі загальні символи із вказівкою для них числа спільності.