4.2 Указание к решению задачи № 2

На формате А3 в левой стороне листа наметить оси координат и из прил. 2 согласно своему варианту взять координаты точек A, B, C, D, E, K – вершин треугольников. Во всех вариантах методика решения одинакова. Линия пересечения двух треугольников строится по точкам пересечения сторон первого треугольника с плоскостью второго треугольника или сторон второго треугольника и плоскостью первого треугольника.

Решение также получается, если данные плоскости пересекаются двумя вспомогательными плоскостями частного положения (уровня или проецирующими).

Образец выполнения задачи № 2 приведен в прил. 5.

Последовательность решения задачи следующая:

1. Проведем фронтально-проецирующую плоскость через сторону АВ ∆ АВС.

Горизонтальный след плоскости совпадает с :

П₁ (α₁ ≡ А₁В₁).

2. Плоскость пересекает сторону ED ∆ DEK в точке 1, а сторону ЕК в точке 2. α ∩ Е₁D₁=1₁, α ∩ Е₁К₁=2₁.

Определим фронтальную проекцию точки 1₂, проведя линию связи до Е₂D₂. Аналогично определяем построение точки 2:

∆DEK = 1–2,

Линия (1−2) – это линия пересечения плоскости α. С плоскостью ∆ dek.

3. Построенная линия (1-2) пересекает сторону ∆DЕK в точке

М (М₁, М₂). По линии связи находим горизонтальную проекцию точки М – М₁:

(1 – 2) АВ = М; А₂В₂ ∩ 1₂ – 2₂ = М₂;

АВ ∆DEK = М. (М₁; М₂).

4. Вторую точку N пересечения стороны DK EDK с плоскостью

∆ АВС находим с помощью фронтально–проецирующей плоскости , проведенной через сторону DK.

Фронтальный след ₂ плоскости совпадает с D₂K₂:

DK П₂, ( ₂ = D₂K₂).

5. Плоскость пересекает сторону АВ ∆ АВС в точке 3;

β₂ ∩ А₂В₂ = 3₂, а сторону АС – в точке 4. Определим горизонтальную проекцию точки 3, проведя линию связи до А₁В₁.

∆АВС = 3–4.

6 Линия (3−4) – это линия пересечения плоскости β с плоскостью

∆ АВС. Построенная линия (3−4) пересекает сторону ∆ DEK в точке N (N₁; N₂). По линии связи находим фронтальную проекцию точки N – N₂:

(3 – 4) DK = N; D₁K₁ 3₁-4₁ = N₁;

DK ∆АВС = N (N₁; N₂).

7 Найденные точки М и N принадлежат линии пересечения треугольников АВС и DEK:

∆ ЕDK ∆АВС = МN.

8 Используя метод «конкурирующих точек», определяем видимость на

комплексном чертеже:

а) определим видимость на П₂.

Рассмотрим две скрещивающиеся прямые АВ и ЕD. Проведем горизонтально – проецирующую прямую (1–7), которая пересекает сторону АВ в точке 7, а сторону ЕD в точке 1. Координаты точек по Z разные – Z₁>Z₇, следовательно, точка 1 стороны ЕD наиболее удалена от плоскости проекций П₂ и будет видимой на П₁, поэтому сторона ЕD на П₂ − видимая.

На :

а)

Так как Z₁>Z₇, то (∙) 1 – видима на П₁, значит и ЕD видимая на П₂, Е₁D₁ – видимая.

б) Определим видимость на П₂.

Проведем фронтально-проецирующую прямую (5–6), которая пересекает сторону ЕК в точке 6, а сторону АВ в точке 5. Так как У₅>У₆, то устанавливаем, что точка 5 прямой АВ дальше отстоит от плоскости проекций П₂ и будет видимой на П₂, следовательно, прямая АВ будет видимой на П₂ до линии пересечения, т. е. до фронтальной проекции точки М – М₂.

На П₂:

б) 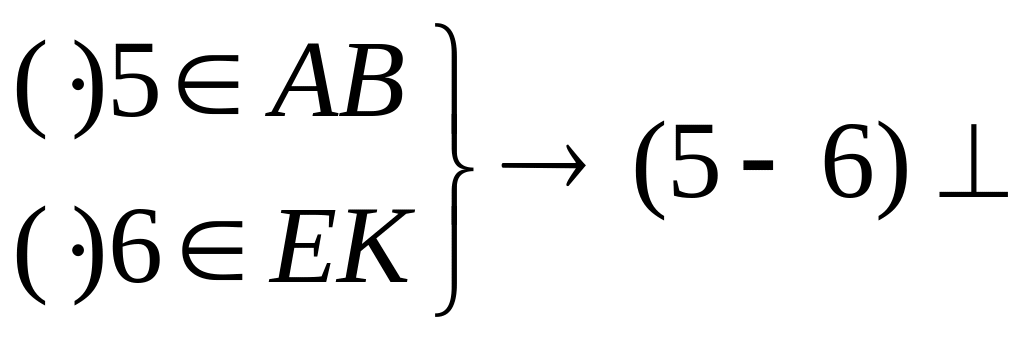П₂

Так как У₅>У₆, то 5 – видимая на П₂ , значит и АВ – видимая на П₂, А₂В₂ – видимая.

4.3 Указания к решению задачи № 3

На формате А3 в левой стороне листа дать изображение многогранника в прямоугольных проекциях с указанием размеров.

Образец выполнения задачи «Построить аксонометрическую проекцию заданного многогранника» приведен в прил. 6.

Для построения аксонометрической проекции данного многогранника используем стандартную прямоугольную изометрическую проекцию согласно ГОСТ 2.317-69.

Положения аксонометрических осей показано на примере в верхнем правом углу (оси расположены под углом в 120 ).

Искажение линейных размеров по осям X, Y и Z выбираем приведенные, т. е. равные 1.

В правой стороне листа нанесем аксонометрические оси и в соответствие с осями, указанными на чертеже многогранника в прямоугольных проекциях, построим нижнее основание, расположив таким образом, чтобы размер 70 мм отложить по оси Х, а размер 40 мм по оси Y. Стороны нижнего основания многогранника будут параллельны аксонометрическим осям.

Из центра нижнего основания отложим высоту многогранника по оси Z, равную 80 мм. Верхнее основание строится аналогично нижнему с меньшими размерами.

Варианты заданий к задаче «Построить аксонометрическую проекцию заданного многогранника» даны в прил. 3, с. 18–20.