37. Запишите формулы прямого и обратного дпф.

ПДПФ:

ОДПФ:

38. (В тестовом задании будут фигурировать конкретные числовые значения) Частота дискретизации сигнала равна … Гц, размерность ДПФ N = … . Какой частоте соответствует результат вычисления ДПФ, имеющий индекс n = … (нумерация начинается с нуля)? Привести соответствующие расчеты.

Будет дано: , . Найти:

39. (В тестовом задании будут фигурировать конкретные числовые значения) Частота дискретизации сигнала равна … Гц, размерность ДПФ N = … . Какой (с каким номером n) элемент ДПФ соответствует частоте … Гц? (Нумерация элементов ДПФ начинается с нуля.) Привести соответствующие расчеты.

Будет дано: , . Найти:

40. В чем заключается основная идея алгоритма быстрого преобразования Фурье с прореживанием по частоте?

При прореживании по частоте вычисления организуются следующим образом:

1. Из исходной последовательность длиной N (должно быть четное число) получаются две последовательности и длиной N/2 согласно следующим формулам:

,

2. ДПФ последовательности дает спектральные отсчеты с четными номерами, ДПФ последовательности -- с нечетными:

,

.

Делить исходную последовательность можно на любое количество частей. Т.О. данный алгоритм позволяет уменьшить число операций в случае любого N, не являющимся простым числом. Степень ускорения зависит от числа фрагментов последовательности и является максимальной при делении на две части. Наибольшая степень ускорения может быть достигнута при N = 2^k.

41. В чем заключается основная идея алгоритма быстрого преобразования Фурье с прореживанием по времени?

Пусть N – четное число. Выделим из формулы ДПФ 2 слагаемых, соответствующих элементам исходной последовательности с четными и нечетными номерами:

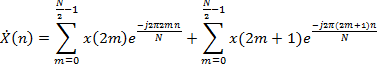
Обозначим y(m)=x(2m) и z(m)=x(2m+1), а также вынесем из второй суммы общий множитель

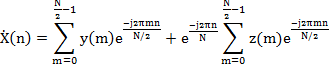
Эти 2 суммы представляют собой ДПФ последовательностей {y(m)} (отсчеты с четными номерами) и {z(m)} (отсчеты с нечетными номерами). Каждое из этих ДПФ имеет размерность N/2. Таким образом: , где и – ДПФ, соответственно последовательностей отсчетов с четными и нечетными номерами.

Так как ДПФ размерности N/2 дает лишь N/2 спектральных коэффициентов, непосредственно использовать последнюю формулу можно только при 0 ≤ n<N/2. Для остальных n (N/2 ≤ n<N) следует воспользоваться периодичностью спектра дискретного сигнала (и, соответственно, периодичностью результатов ДПФ):

Для n ≥ N/2 формула представляется в виде:

42. Что такое «бабочка» в алгоритмах бпф?

«Бабочка» БПФ с прореживанием по времени и ее структурная схема:

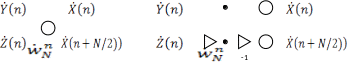
«Бабочка» БПФ с прореживанием по частоте и ее структурная схема:

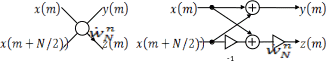
43. Что является математической основой алгоритмов бпф?

Схему БПФ (для 8-точечного БПФ) можно представить как каскадное выполнение нескольких элементарных операций. Каждый каскад реализует некое линейное преобразование последовательности чисел; математически оно может быть представлено как умножение вектора-столбца слева на матрицу преобразования. Общая матрица ДПФ формируется как произведение матриц, соответствующих отдельным каскадам: .

Первый каскад (А₁) – это просто перестановка входных отсчетов в другом порядке. Следующие три каскада однотипны, каждый из них реализует 4 «бабочки», отличаются только тем, какие пары входных/выходных отсчетов используются для «бабочек» и чему равны множители (комплексные экспоненты).

При реализации алгоритма БПФ производится факторизация матрицы преобразования, в результате чего она оказывается представленной в виде произведения разреженных матриц, лишь малая доля элементов которых отлична от нуля. Т.е. происходит ускорение вычислений.