1. (В тестовом задании будут фигурировать конкретные числовые значения) Гармонический сигнал с частотой … Гц дискретизируется с частотой … Гц. Чему равна частота (минимальная из возможных) получившегося дискретного гармонического сигнала? Привести соответствующие расчеты.

Вопрос имеет смысл только если не вып условие т Котельникова, те fo>fн, т е имеют место «ложные частоты». Частота ложно составляющей равно абсолютному значению наименьшей разности между частотой аналогового сигнала и частотой,кратной частоте дискретизации.

2. Как рассчитывается спектральная функция дискретного сигнала {x(k)}? Приведите соответствующую формулу, считая период дискретизации равным T.

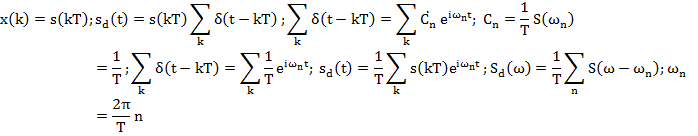
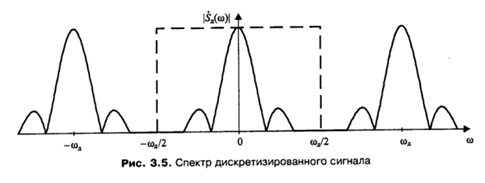
3. Приведите формулу, связывающую спектры аналогового и дискретизированного сиг-налов.

4. Что такое «ложные частоты» (aliasing)? В каких случаях они появляются?

«Ложные частоты»- это частотные составляющие в дискретном сигнале, не содержащиеся в исходном аналлоговом сигнале, появляющиеся при невып условия т Котельникова, те fo>fн.

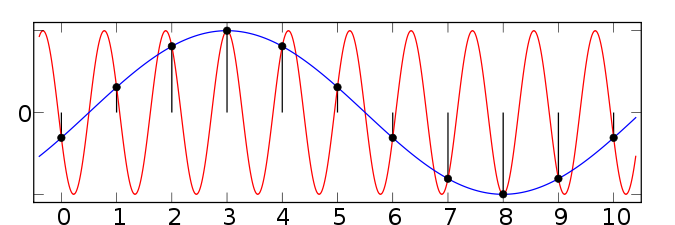
5. Каким образом последовательность дискретных отсчетов представляется в виде функции времени для введения понятия спектральной функции дискретного сигнала?

С математической т зрения это означает умножение функции на гребневую функцию – последовательность импульсов Кронекера

6. Изобразите схему квадратурной дискретизации узкополосного радиосигнала. Чему равна минимально возможная частота дискретизации сигнала в этом случае.

Есть узкополосный сигнал: S(t)=A(t)cos(w₀t +φ(t))

Схема квадратурной дискретизации:

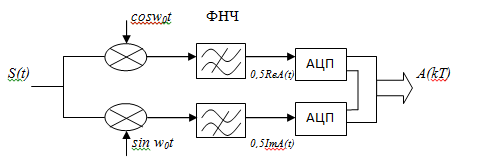
Минимальная частота дискретизации равна ∆w, т.е. ширине спектра сигнала S(t).

7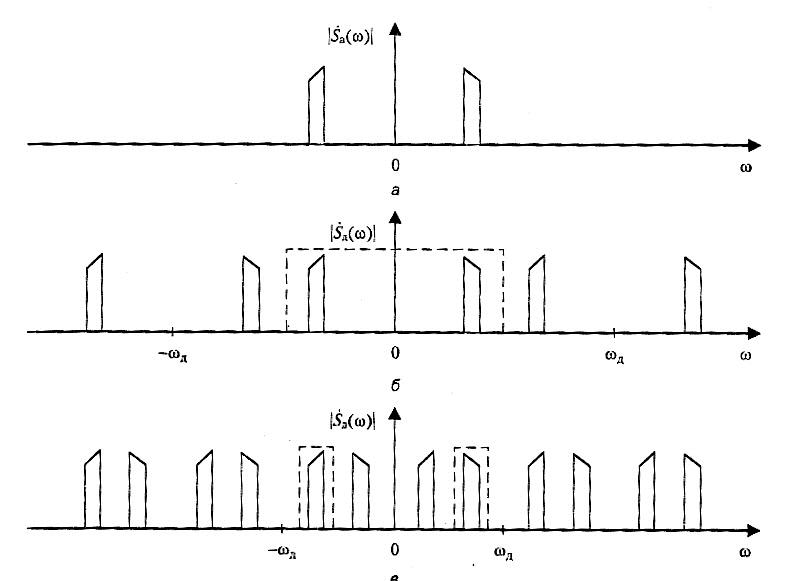 . В чем заключается идея субдискретизации? Приведите неравенства для выбора возможных частот дискретизации узкополосного сигнала.

Субдискретизация - Дискретизация сигнала с частотой ниже, чем выбранная по теореме Котельникова. Используется, когда спектр сигнала ограничен не только сверху, но и снизу.

При обычном подходе частота дискретизации не должна превышать 2f₂. В результате возникающие при дискретизации сдвинутые копии спектра сигнала располагаются как показано на рисунке б. Но для точного восстановления сигнала по его дискретным отсчетам необходимо лишь обеспечить отсутствие перекрытия сдвинутых копий спектра. В данном случае это дает дополнительные возможности для выбора частоты дискретизации. Определим условия, при которых возможна дискретизация сигнала таким образом, при некотором целом k зеркальная половина спектра должна оказаться расположена между k-й и (k+1)-й сдвинутыми копиями спектра (рис в.). Отсюда получаем:

- f₁+ kf_д<f₁; -f₂+(k+1) f_д>f₂; преобразуем в двойное неравенство: 2f₂-f_д<kf_д<2f₁. Отсюда следует: 2f₁>2f₂-f_д =>f_д>2(f₂-f₁). Таким образом частота дискретизации ограничена снизу удвоенной шириной спектра сигнала. Определим максимально возможное значение k: k<2f₁/f_д<f₁/f₂-f_1.

8.Чему равна минимально возможная частота субдискретизации узкополосного сигнала? При каком условии она может быть достигнута?

Субдискретизация - Дискретизация сигнала с частотой ниже, чем выбранная по теореме Котельникова. Используется, когда спектр сигнала ограничен не только сверху, но и снизу.

О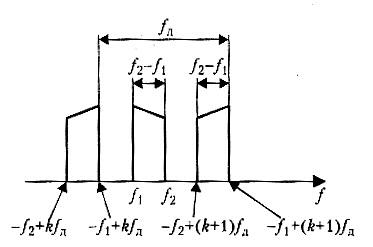 пределим условия, при которых возможна дискретизация сигнала таким образом. При некотором целом k зеркальная половина спектра должна оказаться расположена между k-й и (k+1)-й сдвинутыми копиями спектра. Отсюда получаем:

- f₁+ kf_д<f₁; -f₂+(k+1) f_д>f₂; преобразуем в двойное неравенство: 2f₂-f_д<kf_д<2f₁. Отсюда следует: 2f₁>2f₂-f_д =>f_д>2(f₂-f₁). Таким образом частота дискретизации ограничена снизу удвоенной шириной спектра сигнала. Определим максимально возможное значение k: k<2f₁/f_д<f₁/(f₂-f₁)_.

Для всех целых k, не превышающих это значение определим диапазон возможных значений частоты дискретизации: 2f₂/(k+1)<f_д<2 f₁/k.

9.Как изменится z-преобразование дискретного сигнала, если последовательность отсчетов зеркально перевернуть вдоль временной оси?

Пусть x(k)↔X(z), тогда y(k)=x(-k).

Y(z)=∑x(-k)z^-k=∑x(m)z^m = ∑x(m)(z^-1)^-m = X(z^-1)

10.Как изменится z-преобразование дискретного сигнала, если у отсчетов с нечетными номерами поменять знак?

Пусть x(k)↔X(z)

y(k) = …x(-2), -x(-1), x(0), -x(1), x(2)

y(k)= (-1)^kx(k)

Y(z)= ∑(-1)^kx(k)z^-k = ∑x(k)(-z)^-k =X(-z)

11. Как изменится z-преобразование дискретного сигнала, если у отсчетов с четными номерами поменять знак?

исходная последовательность: …,x(0),x(1),x(2),x(3),… =>x(k)

измененная: …,-x(0),x(1),-x(2),x(3),… => y(k)

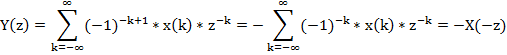
12. Как изменится z-преобразование дискретного сигнала, если между его отсчетами вставить по N - 1 отсчетов с нулевыми значениями?

исходная последовательность: …,x(-1),x(0),x(1),… =>x(k)

измененная: …,x(-1), ,x(0), ,x(1),… =>y(k)

N - 1 N - 1

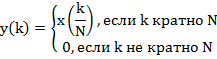
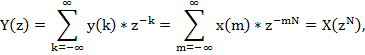
где

13. Как на структурных схемах дискретных устройств обозначается блок, осуществляющий задержку дискретного сигнала на один отсчет? Почему?

Б лок, осуществляющий задержку дискретного сигнала на один отсчет на схемах дискретных устройств обозначается как:

Смысл такого обозначения следует из второго свойства Z-преобразования:

т.е. задержка на один отсчёт соответствует умножению на .

14. Что такое дискретный белый шум? Чему равны его дисперсия и корреляционная функция? Является ли он физически реализуемым? Почему?

ДБШ - стационарный дискретный случайный процесс, отсчёты которого некоррелированы друг с другом:

где - дисперсия ДБШ. ДБШ является физически реализуем, т.к., в отличие от случая аналогового белого шума, его дисперсия не является бесконечной. Корреляционная матрица ДБШ будет иметь диагональнуюстуктуру:

15. Что такое «всепропускающий фильтр» (фазовый фильтр)? Какими соотношениями связаны друг с другом нули и полюсы функции передачи таких фильтров?

Всепропускающими (allpass) называют фильтры, АЧХ которых равна 1 на всех частотах. Такие фильтры меняют только фазы гармоник. Условия, при которых фильтр будет всепропускающим следующие:

1)число нулей равно числу полюсов,

2)значения нулей являются обратными и комплексно-сопряженными по отношению к полюсам,

3)коэффициент усиления фильтра равен произведению модулей полюсов фильтра.

16. Что такое «всепропускающий фильтр» (фазовый фильтр)? Какими соотношениями связаны друг с другом коэффициенты полиномов числителя и знаменателя функции передачи таких фильтров?

«Всепропускающий фильтр» – фильтр, АЧХ которого равна единице на всех частотах; изменяются только фазы спектральных составляющих входного сигнала.

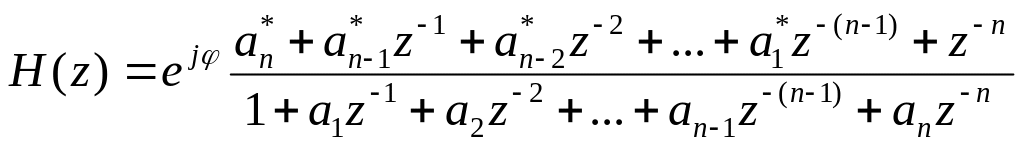, векторы коэффициентов полиномов числителя и знаменателя функции передачи связаны между собой комплексным сопряжением и зеркальным отражением (то есть имеют противоположный порядок следования элементов).

17. Запишите формулу, описывающую функцию передачи дискретной системы в виде суммы простых дробей (считать, что кратных полюсов система не имеет). Запишите формулу для импульсной характеристики дискретного фильтра, выраженную через параметры этих простых дробей.

, где p_i – полюсы, r_i– вычеты

,

18. Сформулируйте условие устойчивости дискретного фильтра.

Система является устойчивой, если при любых начальных условиях свободные колебания являются затухающими, то есть если при x(k) = 0 Для этого ИХ должна быть затухающей .Окончательно: чтобы дискретный фильтр был устойчив, полюсы функции передачи должны находиться на комплексной плоскости внутри круга единичного радиуса.

19. Запишите формулы, описывающие дискретную систему в пространстве состояний. Однозначным ли является представление системы параметрами пространства состояний? Почему?

s(k + 1) = As(k) + Bx(k)

y(k) = Cs(k) + Dx(k)

s(k) – вектор состояния; x(k) и y(k) – отсчеты входного и выходного сигналов; A, B, C и D – параметры, описывающие систему. A – матрица NxN, B – столбец Nx1, C – строка 1xN, D – скаляр 1x1.

Данное представление не является однозначным, поскольку зависит от выбора вектора состояния.

20. Как выразить функцию передачи дискретной системы через параметры пространства состояний? Приведите соответствующую формулу.

H(z) = C(zI- A)^-1B+ D

21. Запишите функцию передачи дискретного фильтра 2-го порядка. Каковы условия устойчивости такого фильтра? (Фильтр считать вещественным.)

Условие устойчивости: полюсы ФП меньше единицы по модулю.

Для вещ. Фильтра:

21. Запишите формулу для функции передачи резонатора 2-го порядка, настроенного на частоту ₀. Что регулирует оставшийся в формуле свободный параметр? Какие значения он может принимать при условии сохранения устойчивости фильтра?

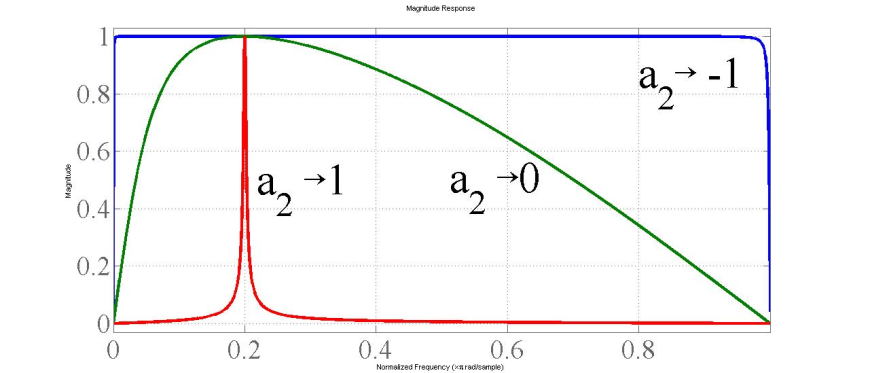
Оставшийся параметр регулирует ширину полосы пропускания резонатора. Чтобы система была устойчивой, необходимо выполнение условия .

21. Запишите формулу для функции передачи режекторного фильтра 2-го порядка, настроенного на частоту ₀. Что регулирует оставшийся в формуле свободный параметр? Какие значения он может принимать при условии сохранения устойчивости фильтра?

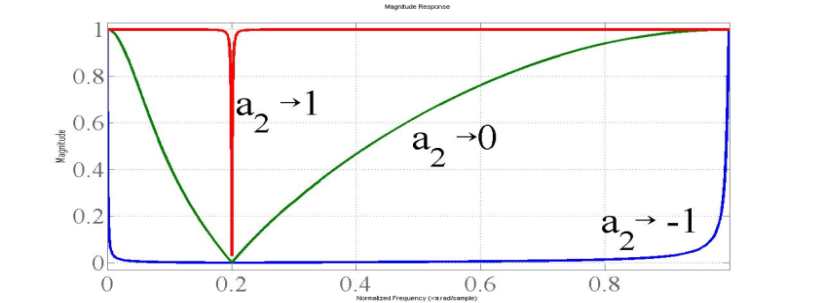
Оставшийся параметр регулирует ширину полосы задерживания режектора. Чтобы система была устойчивой, необходимо выполнение условия

21. Что такое симметричный нерекурсивный фильтр с четной симметрией? Какие ограничения на значения частотной характеристики накладывает данный тип симметрии?

Н ерекурсивный фильтр - фильтр, в котором для вычисления очередного выходного отсчета не используются предыдущие отсчеты выходного сигнала.

Под симметрией нерекурсивного фильтра подразумевается симметрия его импульсной характеристики. При четной симметрии для всех

Ограничения на значения ЧХ:

четный порядок фильтра	нечетный порядок фильтра