15.3.4. Кольцевые счетчики

Кольцевые счетчики представляют собой группу последовательно соединенных и замкнутых в кольцо JK- или D-триггеров (выход последнего подключен к информационному входу первого). В них под воздействием импульсов, поданых на общий для всех триггеров вход синхронизации, осуществляется перемещение одной или нескольких логических единиц от разряда к разряду.

Если замкнуть прямой выход последнего триггера на информационный вход первого, то получается кольцевой счетчик с коэффициентом счета K_с = n, где n - количество триггеров (разрядов) в счетчике. Если первый триггер счетчика находится в состоянии 1, а последний – в состоянии 0, то тактовые импульсы вызовут последовательное перемещение 1 от одного разряда к другому.

Рис. 15.14. Пятиразрядный счетчик Джонсона:

схема (а), таблица истинности (б); ИС 564ИЕ8: УГО (в), таблица истинности (г)

Разновидностью кольцевых счетчиков является счетчик Джонсона, в котором информационный вход первого триггера соединен не с прямым выходом, а с инверсным выходом последнего триггера. В счетчике Джонсона, как и в других кольцевых счетчиках, могут быть сбои, вызванные помехами. Например, если под действием помехи исчезнет записанная в счетчике единица, то все триггеры окажутся в нулевом состоянии и счетчик работать не сможет. На рис. 15.14, а приведена схема пятиразрядного кольцевого счетчика Джонсона с дополнительными ЛЭ DD6, DD7, которые обеспечивают устранение сбоев.

Как следует из таблицы истинности счетчика (рис. 15.14, б), когда на вход счетчика поступают тактовые импульсы, то вначале все разряды счетчика заполняются единицами, а затем - нулями. В результате коэффициент счета счетчика Джонсона составляет К_с = 2∙n, то есть в два раза больше, чем у рассмотренного кольцевого счетчика. Код, в котором работает счетчик Джонсона, называется кодом Либау - Крейга.

В состав ИС 564ИЕ8 (рис. 15.14, в) входят пятиразрядный счетчик Джонсона и дешифратор, который преобразует код Либау-Крейга в десятичный, то есть обеспечивает на выходах сигнал «1 из 10». Режимы работы этого счетчика - делителя показаны на рис. 15.14, г. Счетчик имеет два счетных входа L, C и вход «сброса» R, который обладает приоритетом перед другими входами. По мере счета на каждом из выходов поочередно возникают сигналы высокого уровня.

В процессе работы счетчика на выходе переноса Р формируется последовательность импульсов со скважностью Q = 2 и частотой f = f_вх /10. Выход Р используется для подключения к одному из счетных входов следующего аналогичного счетчика второй декады. Если требуется уменьшить К_с в пределах одной ИС, то вход R соединяется с надлежащим выходом.

ИС 564ИЕ9 отличается от рассмотренной ИС наличием восьми выходов (1 из 8) вместо десяти и частотой сигнала переноса f = f_вх /8. Эти счетчики применяются в качестве распределителей импульсов.

15.3.5. Программируемые счетчики

Счетчики, у которых коэффициент счета задается с помощью набора внешних электрических сигналов, называются программируемыми. Их чаще всего выполняют на основе счетчиков с предварительной записью. В таких счетчиках с помощью внутренней логики выполняется автоматическая перезапись заданного числа после проведения каждого цикла счета. Подав на входы установки коэффициента счета напряжения, соответствующие логическим 1 и 0, удается получить требуемый коэффициент счета и, если это требуется, оперативно изменять его.

В качестве примера выполнения программируемого счетчика можно привести ИС 564ИЕ15 (рис. 15.15, а). Основу ИС составляют четыре четырехразрядных вычитающих счетчика с параллельной записью информации. Первый счетчик состоит из двух секций: секции множителя тысяч Р_т и секции остатка Р_о. Каждая секция имеет переменный коэффициент деления входного кода, которая задается преобразователем кода множителя К. Три остальных счетчика служат для формирования чисел множителей: сотен Р_с, десятков Р_д, и единиц Р_е.

ИС 564ИЕ15 имеет 21 вход. Из них 16 входов D1 – D16 служат для установки кода, соответствующему нужному коэффициенту деления К_д частоты входного сигнала, подаваемого на счетный вход С. Кроме этого, имеется вход выбора режима счета М и три входа для задания кода множителя К (К1, К2, К3). Программируемый счетчик работает в режимах, приведенных на рис. 15.15, б.

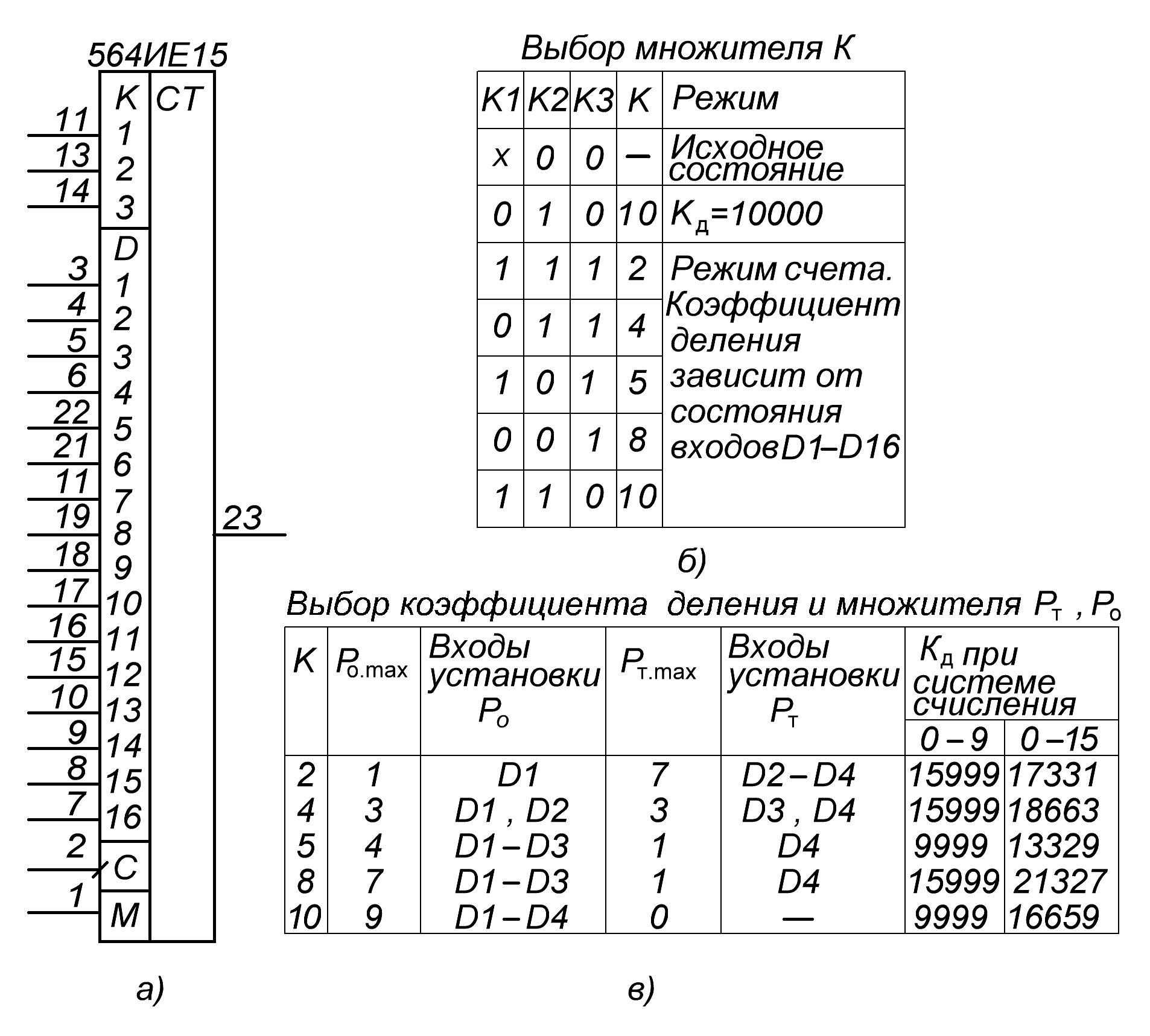
Рис. 15.15. ИС 564ИЕ15:

УГО (а); режимы работы (б); выбор коэффициента деления и множителей P_т, P_о (в)

1. Режим установки счетчика в исходное состояние. В этом режиме осуществляется запись входного кода, поданного на входы D, и запрещается счет на выходе ИС. Для установки ИС в исходное состояние необходимо задать К2 = К3 = 0 в продолжение не менее трех периодов входных импульсов.

Следовательно, минимальный коэффициент деления во всех других режимах составит К_{д min} = 3.

2. Режим многократного счета осуществляется при М = 0. В этом режиме на выходе ИС формируются периодические импульсы с частотой f = f_c /K_д, где f_c – частота входного сигнала.

3. Режим однократного счета происходит при М = 1. Этому режиму обязательно предшествует режим установки счетчика в исходное состояние. После поступления на вход импульсов в количестве K_д выход счетчика переходит из состояния 0 в состояние 1 и не меняется с приходом последующих импульсов. При этом счет во внутренних счетчиках продолжается и, если установить М = 0, то счетчик перейдет в режим многократного счета.

4. Режим счета с K_д = 10000 осуществляется при подаче на вход К комбинаций К1 = 0, К2 = 1, К3 = 0 независимо от кодовых комбинаций на входах D. Этот режим возможен как при многократном, так и при однократном счете.

Коэффициент деления в режимах многократного и однократного счета зависит от сигналов на входах D, K и определяется выражением

K_д = K∙(1000∙P_т+ 100∙P_с+ 10∙P_д+ P_е) + P_о . (15.1)

Множитель К определяется кодовыми комбинациями на входах К1, К2, К3 и может принимать только определенные значения, которые приведены в таблице (рис. 15.15, б). Множитель тысяч P_т может иметь значения от 0 до 7, но не более своего максимального значения P_т.max (рис. 15.15, в). Остаток от деления P_о может принимать значения от 0 до 9, но не более своего максимального значения P_о.max (рис. 15.15, б). Максимальные значения P_т.max, P_о.max определяются значением множителя К. Множители P_с, P_д, P_e могут быть представлены как в десятичной (0 - 9), так и в шестнадцатеричной (0 - 15) системах счисления.

Числа множителей Р должны быть представлены в виде натурального двоичного кода. Эти двоичные числа, в виде логических уровней напряжения, подаются на входы ИС следующим образом: P_т на D2 - D4, P_с на D13 - D16, P_д на D9 - D12, P_e на D5 - D8; P_о на D1 - D4. Распределение входов D2 - D4 между числами P_т и P_о регламентируется таблицей (рис.15.15, в). Для каждого двоичного набора чисел Р младшему разряду числа соответствует вход D с меньшим номером. Максимальный коэффициент деления зависит от выбранного множителя К и системы счисления множителей P_с, P_д, P_e. Он не должен превышать значений, указанных в таблице (рис.15.15, в). Порядок установки множителей поясним на примерах.

Пример 1. Пусть требуется задать K_д = 8479 при К = 5 и десятичной системе счисления множителей P_с, P_д, P_e. Тогда K_д /К = 8479/5 = 1695+4. В соответствии с выражением (15.1), множители Р равны

P_т = 1; P_с = 6; P_д = 9; P_e = 5; P_о = 4.

На входе преобразователя кода множителя К (рис. 15.15, б) устанавливаем K1 = 1; K2= 0; K3 = 1. Значения множителей Р и соответствующий им двоичный код приведены в табл. 15.3.

Таблица 15.3. Двоичный код множителей Р при системе счисления 0 - 9

Pт=1	Pс = 6				Pд = 9				Pe= 5				Pо= 4
D4	D16	D15	D14	D13	D12	D11	D10	D9	D8	D7	D6	D5	D3	D2	D1
1	0	1	1	0	1	0	0	1	0	1	0	1	1	0	0

Пример 2. Пусть требуется задать K_д = 17241 при К = 2 и шестнадцатеричной системе счисления. Тогда K_д /К = 17241/2 = 8620 + 1. Так как при К = 2, согласно рис. 15.15, в, P_т ≤ 7, то выбираем P_т = 7, а восьмую тысячу переносим в разряд сотен. Так как при этом образуется P_с = 16, что превышает допустимый предел P_c.max ≤ 15, то шестнадцатую сотню переносим в разряд десятков, т.е. выбираем P_c = 15, P_д = 10+2 = 12.

Следовательно, разложение числа 17241, согласно выражению (15.1), будет иметь вид

17241 = 2∙(1000∙7 + 100∙15 + 10∙12 + 0) + 1.

На входе преобразователя кода устанавливаем К1 = 1; К2 = 1; К3 = 1. Значения множителей Р и соответствующий им двоичный код приведены в табл. 15.4.

Таблица 15.4. Двоичный код множителей Р при системе счисления 0 - 15

Pт = 7			Pс = 15				Pд = 12				Pe= 0				Pо=1
D4	D3	D2	D16	D15	D14	D13	D12	D11	D10	D9	D8	D7	D6	D5	D1
1	1	1	1	1	1	1	1	1	0	0	0	0	0	0	1

Выпускаемая промышленностью номенклатура счетчиков ИС серии КР1554 приведена в табл. 15.5.

Таблица 15.5. Счетчики серии КР1554

Обозначение	Функциональное назначение
КР1554ИЕ6	Двоично-десятичный синхронный реверсивный счетчик
КР1554ИЕ7	Четырехразрядный двоичный синхронный реверсивный счетчик
КР1554ИЕ10	Четырехразрядный синхронный счетчик
КР1554ИЕ18	Четырехразрядный синхронный счетчик с синхронным сбросом
КР1554ИЕ19	Два четырехразрядных асинхронных счетчика