1.Цифро-аналоговые преобразователи
10.1. Представление числа в виде кода
Всякое число представляется набором цифр. Способ представления чисел цифрами характеризует систему счисления (код). Наибольшее распространение получили позиционные системы счисления, в которых число, эквивалентное записанной цифре, определяется как значением этой цифры, так и её положением (позицией) среди других цифр. Основание системы счисления - это число, равное количеству цифр, необходимых для выражения всех чисел в пределах одного разряда.
Положительное число из n разрядов в позиционной системе с основанием a может быть представлено следующим образом:
Xa = xn an-1 + xn-1 an-2 + … + x2 a1 + x1 a0,
где х – любая цифра от 0 до а - 1; здесь первый член представляет старший разряд (СР) числа, а последний – младший (МР).
Десятичная система счисления – типичный пример позиционной системы, например, в этой системе число 573 можно представить как:
57310 =5·102 + 7·101 + 3·100.
В цифровой технике наибольшее применение получил двоичный код, в котором n-разрядное число представляется следующим образом:
X2 = xn 2n-1 + xn-1 2n-2 + … + x2 21 + x1 20,
где коэффициенты x могут принимать два значения: 0 и 1. Разряд с индексом n является старшим, а с индексом 1 – младшим. Соответствие десятичных и двоичных чисел приведено в табл. 10.1.
Таблица 10.1. Соответствие десятичных и двоичных чисел
Десятичное число |
0 |
1 |
2 |
3 |
4 |
Двоичное число |
0·20=0 |
1·20=1 |
1·21+0·20=10 |
1·21+1·20=11 |
1·22+0·21+0·20=100 |
10.2. Коэффициент преобразования цап
Цифро-аналоговый преобразователь (ЦАП) предназначен для преобразования числа, представленного, как правило, в виде двоичного кода, в ток или напряжение, пропорциональные этому числу. Большинство ЦАП составляют преобразователи параллельного двоичного кода в напряжение или ток, осуществляющих деление опорного напряжения или тока. В настоящее время, в связи с развитием микроэлектроники, получили широкое распространение последовательные ЦАП, например, сигма-дельта ЦАП.
Если входной код ЦАП является двоичным, а выходной функцией ЦАП является ток, то выходную функцию ЦАП можно представить в виде
Iвых = Iо (xn 2n-1 + xn-1 2n-2 + … + x2 21 + x1 20) = Iо X,
где n – разрядность входного кодового числа (слова) X; Iо – нормированный входной ток ЦАП.
В этом случае под коэффициентом преобразования ЦАП понимают Iо = Iвых /X. Если выходной функцией ЦАП является напряжение, то коэффициент преобразования имеет вид
Uо = Uвых /X,
где Uо – нормированное входное напряжение ЦАП.
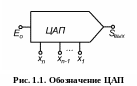
Обычно ЦАП содержит вход для подключения источника опорного напряжения Ео.
Таким образом, ЦАП можно представить в виде, показанном на рError: Reference source not found, где Sвых – выходной ток или напряжение; xn, xn-1, … x1 – цифры двоичного кода.
10.3. Цап с суммированием токов на основе резистивной матрицы типа r–2r
На рис. 1 .1 приведена функциональная схема ЦАП с суммированием токов, в котором использован один источник опорного напряжения Ео и резистивная матрица (РМ) R – 2R. Распределение потенциалов в узлах матрицы не меняется при изменении положения ключей Sn, Sn-1, … S1, поскольку потенциал И–входа ОУ равен потенциалу общей шины. Поэтому входное сопротивление РМ при любом положении ключей равно R.
Рис. 1.1. Функциональная электрическая схема ЦАП (ИС 572ПА1)
Следовательно, ток, втекающий в РМ, равен Iо = Eо /R. Это обстоятельство приводит к последовательному уменьшению вдвое напряжения в верхних узлах схемы по мере их удаления от источника опорного напряжения, поэтому ток, протекающий через резисторы 2R, будет изменяться по двоичному закону.
In = Eо / 2R, In -1= Eо / 4R, …, I1= Eо / (2R·2n-1)
или в общем виде
Ii = Eо / (2R·2n-i) = Eо 2i-n / 2R.
Выходной ток ЦАП будет равен
,
где xi = 1, если ключ Si замкнут на вход ОУ; xi = 0, если ключ Si замкнут на общую шину.
Выходное напряжение ОУ при этом будет равно
. (10.1)
Максимальное значение выходного напряжения ОУ имеет место при всех xi = 1 (все ключи замкнуты на вход ОУ) и определится выражением
Uвых.max = Eо Roc(1 – 2-n) / R= Eо Roc /R - h,
где h – шаг квантования, то есть приращение выходного напряжения при изменении входного кода на единицу младшего разряда (ЕМР); h = Eо Roc /(R·2n).
Как следует из формулы (10.1), выходное напряжение ОУ зависит не только от входного кода Х, но и от напряжения Eо опорного источника. Если к входу опорного источника подключить источник переменного напряжения, то ЦАП в этом случае будет формировать выходной сигнал, пропорциональный произведению входного кода и напряжения, поданного на вход опорного сигнала.
Промышленным аналогом рассмотренной схемы ЦАП является ИС 572ПА1, которая предназначена для преобразования 10-разрядного прямого параллельного двоичного входного кода в ток на аналоговом выходе. Значения основных параметров ИС зависят в первую очередь от точности соблюдения отношений Roc /R = 1 и R /2R = 0,5 для всех звеньев РМ. Поэтому резисторы выполнены в виде идентичных по геометрическим размерам областей, одинаково ориентированных относительно осей кристалла. В качестве резистивного материала использована выращенная на поверхности кристалла методом вакуумного осаждения тонкая плёнка поликремния с высокой стабильностью сопротивления. Транзисторы токовых ключей Sп, Sп-1, … S1 выполнены по КМОП технологии с поликремниевым затвором таким образом, что их сопротивления в проводящем состоянии достаточно малы. Сопротивление ключей первых шести разрядов изменяется по двоичному закону (20, 40, … 640 Ом). Таким способом уравниваются (до 10 мВ) падения напряжения на ключах, что обеспечивает монотонность и линейность переходной характеристики ЦАП.