6.2.2 Вычисление погрешностей при разбивки способом полярных координат
Точность разбивки: средняя квадратическая погрешность в положении точки М на местности относительно разбивочного обоснования складывается:
,
где – СКП построения проектного угла;
– радиан;
–
СКП построения линии заданной проектной
длины;
тфикс – СКП фиксирования точки на местности.
6.3. Вынос в натуру проектных точек способом угловых засечек
6.3.1 Вычисление разбивочных элементов и составление схемы разбивки
Этот способ применяется в тех случаях, когда расстояния от разбивочного обоснования до проектных точек недоступны для непосредственного измерения или построения. Построение выполняется только теодолитом.
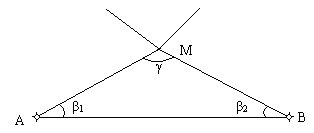
Рис. 5
Исходные данные:
Точки А и В разбивочного обоснования закреплены на местности и известные их координаты.
Проектом даны координаты точки М.
Требуется построить на местности точку М.
Рассчитываются углы β1
и β2. Для этого
решаются обратные геодезические задачи.
Из решения обратной геодезической
задачи между точками А и М находится
дирекционный угол
,
а между точками
ВМ –
.
Вычисляются проектные углы:
,
.
6.3.2 Разбивка сооружений на местности
На местности строятся проектные углы β1 и β2 и в пересечении полученных направлений получается точка М. Углы β при построении должны быть менее 30º, а угол γ при засечке в пределах: 30 < γ < 150.
Для контроля проверяют положение точки М с других точек разбивочного обоснования аналогичным образом.
При этих условиях положение точки М определяется наиболее надежно.
6.3.3 Вычисление погрешностей при разбивки способом угловой засечки
Средняя квадратическая погрешность в положении точки М относительно разбивочного обоснования определяется:
.
где
и
–
СКП построения проектных углов β1
и β2,
тфикс – СКП фиксирования точки М на местности.
6.4. Вынос в натуру проектных точек способом линейных засечек
6.4.1 Вычисление разбивочных элементов и составление схемы разбивки
При этом способе положение проектных точек определяеют только с помощью мерной ленты или рулетки.
Рис. 6
Исходные данные:
Точка А и В разбивочного обоснования закреплены на местности и известны их координаты.
Проектные координаты точки М.
Требуется на местности линейной засечкой определить положение точки М.
Производится расчёт разбивочных данных – расстояния S1 и S2. Их находят из решения обратных задач на координаты по направлениям АМ И ВМ.
6.4.2 Разбивка сооружений на местности
На местности от точек А и В откладывая вычисленные расстояния определяют положением точки М.
При этом, наиболее надежно определится точка М, если расстояния S1 и S2 не превышают длины мерного прибора, а угол при засечке находится в пределах: 30° < γ < 150°.
Если эти условия не соблюдаются при разбивке с точек А и В, то линейную засечку точки М можно выполнить от вспомогательных створных точек K и L.
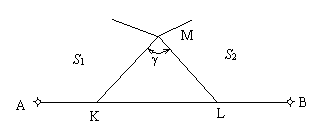
Рис. 7
Координаты створных точек К и L можно задавать наиболее подходящими расстояниями АК и АL. За дирекционный угол принимают дирекционный угол стороны АВ.
На местности створные точки К и L находятся с помощью теодолита и мерной ленты или рулетки.
6.4.3 Вычисление погрешностей при разбивки способом угловой засечки
Ср.кв. погрешность в положении точки М относительно разбивочного, определится по формуле:
.
где и – СКП построения S1 и S2,
тфикс – СКП фиксирования точки М на местности.