58. Спектральная плотность случайных колебаний. “Белый шум” и его свойства.

Спектральная плотность S_x(ω) случайного процесса x(t) определяется как преобразование Фурье корреляционной функции R_x(τ):

Воспользуемся формулой Эйлера

и подставим в S_x(ω):

0

Спектральная плотность является действительной и четной функцией частоты ω, поэтому на графиках она всегда симметрична относительно оси ординат.

Если спектральная плотность известна, то по формуле обратного преобразования Фурье можно найти соответственную ей корреляционную функцию:

Изобразим графически корреляц. функции и спектральные плотности некоторых колебаний.

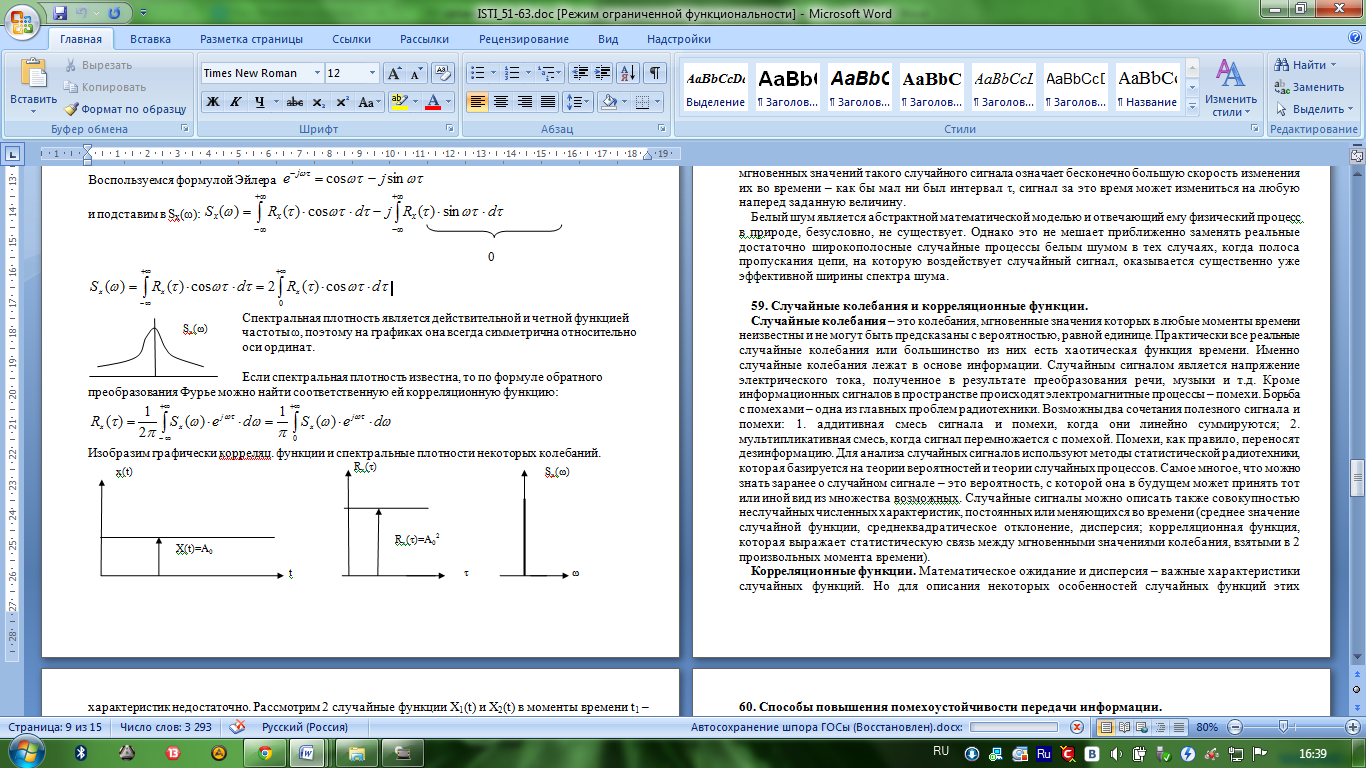
X(t)=Asin(ωt+φ₀) R_x(τ)

(косинусоида)

Белый шум. Для анализа радиотехнических цепей и сигналов большой практический интерес представляет специфический случайный процесс, теоретически имеющий равномерный спектр мощности во всей полосе частот:

(2.121)

Такой идеализированный случайный процесс получил название белый шум по аналогии с белым светом, имеющим в видимой части практически равномерный сплошной спектр.

Определим функцию корреляции белого шума. Используя формулы (2.117) и (2.121), запишем

(2.122)

Средняя мощность белого шума неограниченно велика.

Белый шум является дельта-коррелированным случайным процессом. Некоррелированность мгновенных значений такого случайного сигнала означает бесконечно большую скорость изменения их во времени – как бы мал ни был интервал τ, сигнал за это время может измениться на любую наперед заданную величину.

Белый шум является абстрактной математической моделью и отвечающий ему физический процесс в природе, безусловно, не существует. Однако это не мешает приближенно заменять реальные достаточно широкополосные случайные процессы белым шумом в тех случаях, когда полоса пропускания цепи, на которую воздействует случайный сигнал, оказывается существенно уже эффективной ширины спектра шума.

66. Структурные меры информации.

Важнейшим вопросом в теории информации является установление меры, количества и качества информации.

Структурные меры информации.

При использовании их пользуются количеством содержащихся информационных элементов в информационном дискретном комплексе, связями м-ду ними или комбинациями из них. Под информационным элементом понимают неделимые части – кванты информации, а так же элементы алфавитов в числовых системах. Среди структурных схем различают: геометрическую, комбинаторную, аддитивную (мера Хартли) меры информации.

Геометрическая мера – количество информации определяется путём измерения длины линии, площади или объема геометрической модели в количестве дискретных единиц. Можно определить потенциальную, т.е. максимально возможное количество информации в заданных структурных габаритах, которые называют информационной ёмкостью исследуемой части информационный системы, она может представляться числом показывающем количество квантов в полном массиве информации. Если дискретные отчёты осуществляются через интервалы ∆Х, ∆t, ∆N, то непрерывные координаты распадаются на элементы, кванты, количество которых будет:

m_X=X/∆X; m_Т=T/∆T; m_N=N/∆N;

а количество информации определяемым геометрическим методом :

М= m_X*m_{Т *}m_N;

Комбинаторная мера – количество информации в этой мере вычисляется как количество комбинаторных элементов. В комбинаторике рассматриваются различные меры соединения элементов (сочетание, перестановка, размещение). В комбинаторике возможно в комплексах с неодинаковыми элементами переменными связями или разнообразными позициями. Образование комбинаторики есть одна из форм кодирования. Комбинаторика различает различные виды элементов: сочетание h по l; их возможное число:

перестановки h: P_h=1*2*3…h=h!; размещение из h по l: A^l_h=h!/l! ;

Аддитивная мера – введём понятие глубины h и длинны l числа.

Г лубиной h назовём количество элементов (знаков), содержащихся в принятом алфавите. Глубина числа соответствует основанию системы счисления и кодирования. В каждый момент реализуется один какой-нибудь знак.

Длинной l числа назовём количество повторения алфавита необходимых и достаточных для представления чисел нужной величины. l - соответствует разрядности системы счисления и кодирования. При глубине h и длине l количество чисел выразится Q=h^l , т.е. ёмкость экспонента зависит от числа l. В следствии показательного закона зависимости Q(l) , Q не очень удобная мера для оценки информационный ёмкости, поэтому Хартли ввёл аддитивную двоичную логарифмическую меру, позволяющую вычислить количество информации в двоичных единицах (битах), для этого берётся не само число Q, а его двоичный логарифм: I= log₂Q= log₂h^l= llog₂h; бит.

Он обозначает количество информации по Хартли. Если количество разрядов (длинна l=1) и принять двоичную систему исчисления для которой глубина h=2, то log₂2¹=1 бит.

Это если единица информации принятая в системе оценки, она соответствует одному элементарному событию, которое может произойти или не произойти.

Аддитивная мера удобна тем, что обеспечивает возможное сложение а также пропорционально информационной длине числа l.