2.1.2 Дифференциальный метод

Дифференциальный метод может быть исполь­зован как для ранжированных показателей, так и для исходной вы­борки. В основу метода положены соотношения, опирающиеся на сред­ние значения показателя:

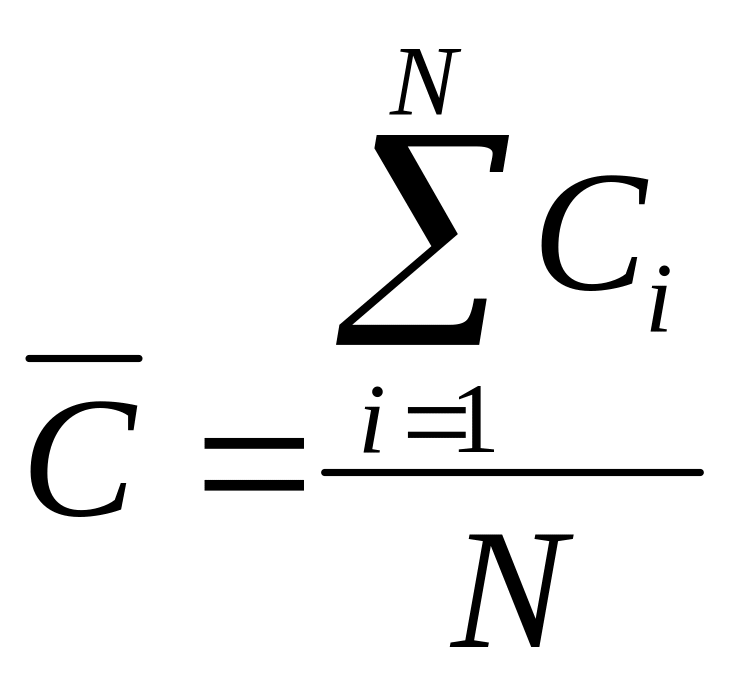(3.3)

где N — объем выборки.

В се мате­риальные ресурсы, количество заявок на которые в шесть и более раз превышает C, включаются в подмножество А. В подмножест­во С включаются все материальные ресурсы, количество заявок на которые в два и более раза меньше C. Все остальные матери­альные ресурсы включаются в подмножество В.

Несомненное достоинство дифференциального метода — простота: нет необходимости ранжировать показатели С_i и строить интегральную (накопленную) зависимость.

2.1.3 Аналитический

Особенность данного метода состоит в том, что полученные значения С_i, ранжируются и располагаются в убывающей последовательности: и в зависимости от последующего способа определения номенклатурных групп представляются в виде графика или в случае приме­нения аналитического способа в табличной форме в виде пар значений ( ;i) для подбора аналитической зависимости.

(3.4)

где i — номер детали, i = 1, i N.

При графическом способе (рис. 1) на оси ординат наносятся значе­ния Q_j, на оси абсцисс — индексы 1, 2,..., N, соответствующие присво­енным номерам позиций номенклатуры. Точки с координатами (Q_j; i) на графике соединяются плавной кривой 00'D, которая в общем случае является выпуклой. Затем проводится касательная LM к интеграль­ной кривой 00'D параллельно прямой OD.

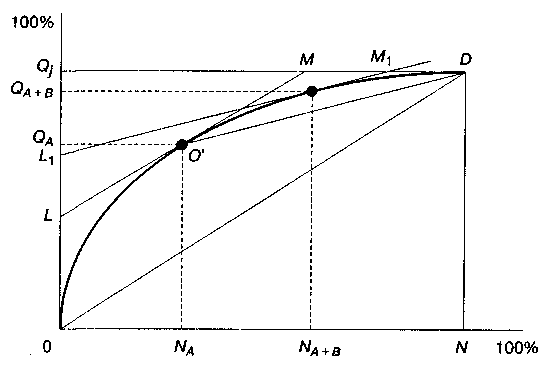
Рис. 1- Определение номенклатурных групп А, В, С (графический способ)

Прямая OD соответствует равномерному распределению показателя q_A для всей номенклатуры:

(3.5)

Абсцисса точки касания О', округленная до ближайшего целого значения, отделяет от всей номенклатуры деталей груп­пу A (N_A), в которую входят позиции номенклатуры с показателями q_t > q_A. Та­ким образом, к группе А относятся все позиции номенклатуры, для которых значение показателя q_i больше или равно среднему значению показателя для всей номенклатуры N. Соответственно ордината точки (Q_A) указывает долю деталей груп­пы А в процентах от величины общего показателя Q_j.

Продолжим деление на группы оставшейся номенклатуры деталей, воспользовавшись вышеописанным приемом. Соединим точку О' с точ­кой D и проведем касательную к кривой O'O''D, параллельную прямой О'D. Абсцисса точки касания О'' делит оставшуюся номенклатуру на группу В и группу С.

Для оставшейся номенклатуры величина осредненного показателя составит:

(3.6)

где N_A— число позиций, вошедших в группу А.

Таким образом, в группу В попадают позиции номенклатуры с по­казателями q_j, подчиняющимися неравенству

Пример 1. В табл. 1 при­ведены данные о 20 позициях продукции, находящейся на складе. До­пустим, что на группы разбивается стоимостной показатель:

С_i = n_iЦ_i , (3.7)

где n_i — количество единиц продукции, ед.; Ц_i — стоимость единицы продукции, руб./ед.

После расчета С_i все позиции номенклатуры располагаются в по­рядке убывания стоимостных показателей. Затем в зависимости от вы­бранного варианта метода ABC производится деление на группы.