1.3. Прогнозирование материалопотока

Для прогнозирования материалопотока и товарооборота склада необходимо подобрать наиболее подходящее из известных матема­тических уравнений функций (прямую, гиперболу, параболу и т. д.). Эти уравнения определяются на основании графиков, которые строятся по отчетным данным (динамическим рядам). Рассмотрим эти уравнения.

Уравнение прямой имеет следующий вид:

(1.3)

где у_х — результативный признак; х — период времени; а и b — параметры прямой.

Нахождение параметров а и b производится на основе выравни­вания по способу наименьших квадратов, которые приводят к сис­теме двух линейных уравнений с двумя неизвестными:

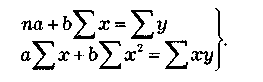(1.4)

Решая это уравнение, находим:

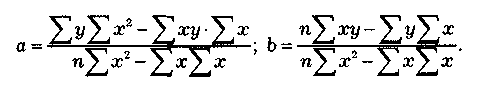(1.4а)

В целях облегчения нахождения параметров а и b систему мож­но упростить. Для этого отсчет времени следует вести так, чтобы сумма показателей времени ряда ( ) была равна нулю. Такая ус­ловность вполне допустима ввиду того, что начало выбирается произвольно.

Чтобы равнялась нулю, в рядах с нечетным числом членов центральный член принимается за нуль, а члены, идущие от цент­ра (в столбце) вверх, получают номера от -1, -2, -3 — со знаком минус, а вниз — +1, +2, +3 — со знаком плюс. Например, ряд со­ставляет 7 членов (вверх-3;-2;-1;; вниз +1;+2;+3). Если число членов ряда четное (на­пример, 6), рекомендуется занумеровать члены верхней половины ряда (от середины) числами -1, -3, -5 и т. д., члены нижней поло­вины (от середины) — +1, +3, +5 и т. д. В обоих случаях = 0.

Если члены динамического ряда получили такую нумерацию, что их сумма оказывается равной нулю, то система уравнений при­нимает вид

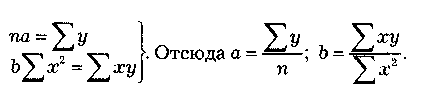(1.5)

Из приведенных формул видно, что для нахождения парамет­ров уравнения прямой необходимо знать величины , , .

Если уровни динамического ряда обнаруживают тенденцию ро­ста по геометрической прогрессии, т. е. прирастают на одинаковое число процентов, выравнивание такого ряда следует проводить по показательной кривой: у_х = аb^х. В этом уравнении х — рассматри­ваемый период, а — начальный уровень ряда (при х = 0), b — темп роста за единицу времени.

Техника выравнивания по показательной кривой аналогична технике выравнивания по прямой.

Кроме выравнивания и прогнозирования по прямой и пока­зательной кривой, на практике часто используются и другие функции.

Например, уравнение параболы второго порядка:

(1.6)

где а, b, с — параметры, которые находятся из системы нормальных уравнений.

Сама система уравнений, получаемая по способу наименьших квадратов, следующая:

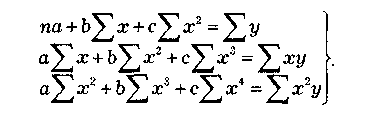(1.7)

Обозначим время таким образом, что = 0. В этом случае нулю будет равно и (как всякая сумма нечетных степеней х). В силу сказанного система нормальных уравнений примет вид:

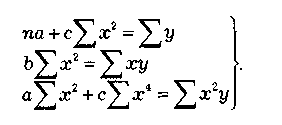
Во втором уравнении:

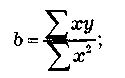(1.9)

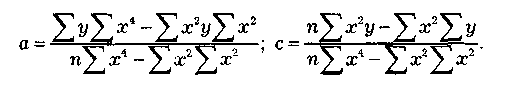(1.10)

Пример 1. За период с 1998 по 2004 г. известен динамический ряд товарооборота регионального склада (табл. 1.3). Сделайте прогноз товарооборота 2007 г.

Таблица 1.3 Товарооборот за период 1998—2004 гг.

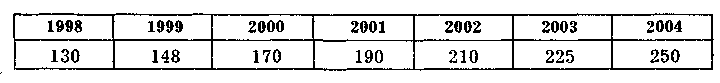
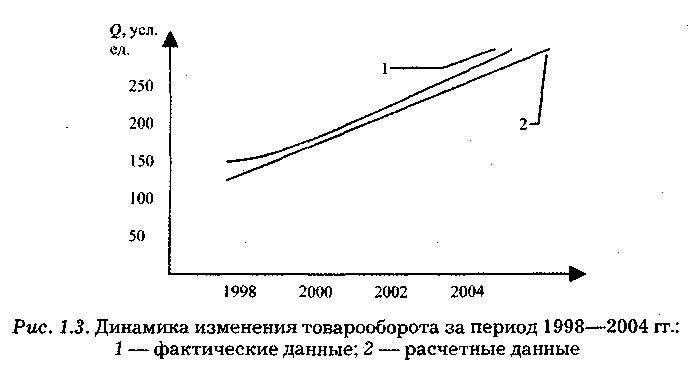
Решение.

По данным табл. 1.3 строим график (рис. 1.4) динамики изменения товарооборота за период 1998—2004 гг. Из этого графи­ка видна тенденция изменения товарооборота. Она идет по прямой линии. Поэтому связь между указанными признаками может быть описана уравнением:

где у_х — товарооборот регионального склада в условных единицах; х — рассматриваемый период; а и b — параметры (табл. 1.4).

Найденные значения подставим в формулы (1.5), получим пара­метры а и b:

Уравнение нашей прямой будет:

Таблица 1.4

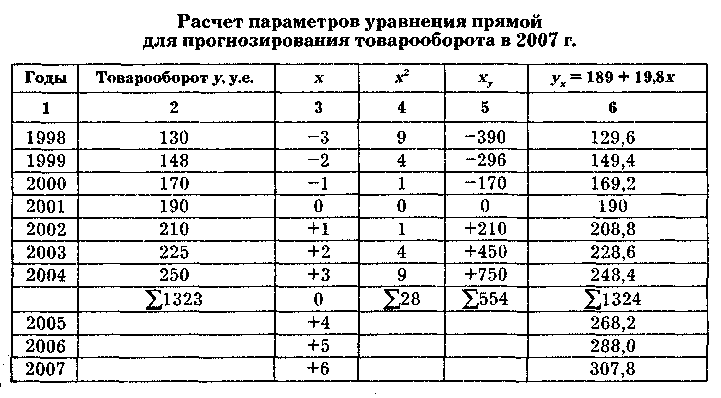
Подсчитаем теоретические уровни ряда для каждого года (гр. 6, табл. 1.4).

Сопоставленные графы 2 и 6 по каждому году показывают весь­ма незначительные отклонения расчетных уровней от фактичес­ких, что подтверждает правильность выбора математического уравнения.

Для прогнозирования товарооборота необходимо продолжить графу 3 (рассматриваемый период) числами, следующими за ука­занным числом. В нашем случае это 3, далее рассматриваемый пе­риод будет 4, 5, 6 и т. д. На 2007 г. х = 6, тогда у₂₀₀₇ = 189 + 19,8 x 6 = 307,8.

Пример 2. За период 1999—2004 гг. известен динамический ряд объема перевозок грузов с регионального склада (табл. 1.5). Сделайте прогноз перевозок в 2007 г.

Таблица 1.5

Исчислим параметры а, Ъ, с по данным табл. 1.6 и формулам (1.9), (1.10).

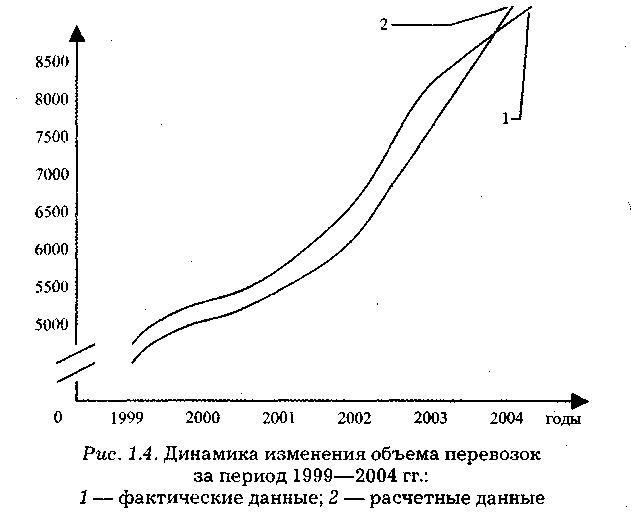
Таблица 1.6 Расчет параметров уравнения параболы для выравнивания и прогнозирования объема перевозок с регионального склада

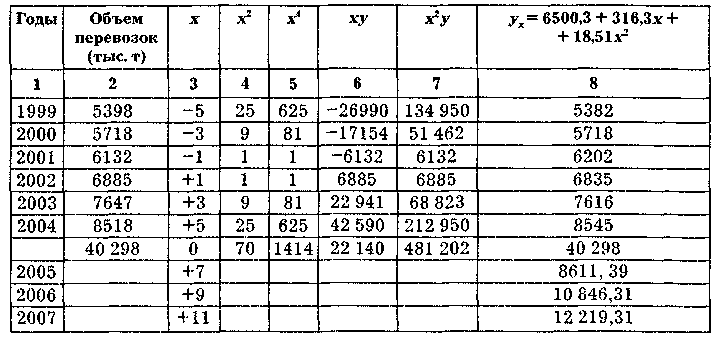
Отсюда: а = (40 298 x 1,414 - 481 202 x 70)/(6 x 1414 - 702) = 6500,3;

b = 22 140/70 = 316,3; с = (6 x 481 202 - 70 x 40 x 40 298)/(6 x 1414 - 702) = 18,51.

Таким образом, уравнение параболы в нашем примере имеет вид:

Подставив в эту формулу конкретные значения х, находим зна­чения у_х для всех членов динамического ряда (гр. 8, табл. 1.6). Сопоставленные графы 2 и 8 показывают незначительные от­клонения теоретических уровней от эмпирических, что свидетель­ствует о правильности выбора уравнения кривой.

В 2007 г. объем перевозки грузов с регионального склада со­ставит: