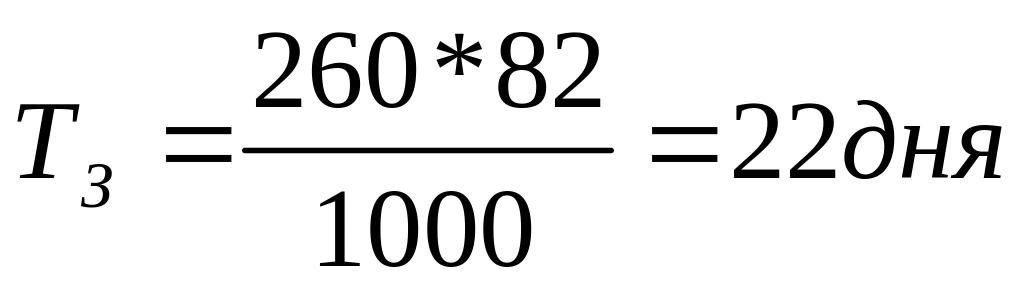1. Основная модель расчета оптимального размера заказа

Наиболее распространенной моделью прикладной теории логистики является модель оптимального или экономичного размера заказа EOQ (Economic Order Quantity). Расчет EOQ производится на основе суммарных общих затрат , которые можно представить в виде функции:

= С_К+С₃+С_Х+С_Д. (4.6)

Затраты на приобретение С_к определяются стоимостью единицы продукции; в свою очередь, стоимость может быть постоянной или пе­ременной при учете оптовых скидок, которые зависят от объема заказа.

Затраты на оформление заказа С₃ представляют собой постоянные расходы, связанные с размещением заказа у поставщиков и его транс­портировкой.

Затраты на хранение запаса С_х отражают затраты на содержание и грузопереработку запаса на складе; затраты С_х включают как про­цент на инвестированный капитал, так и стоимость хранения, содер­жания и ухода.

Потери от дефицита запаса С_Д включают, потенциаль­ные потери прибыли из-за отсутствия запаса, возможные потери из-за утраты доверия покупателей.

Очевидно, что учет различного количества слагаемых в формуле (4.6) приводит к многовариантности расчетных формул для определения EOQ. Рассмотрению некоторых из них посвящен следующий раздел.

При формировании основной модели расчета EOQ в качестве крите­рия оптимизации принимается минимум общих затрат , включаю­щих затраты на выполнение заказов С₃ и затраты на хранение запаса на складе С_х в течение определенного периода времени (год, квартал и т. п.):

(4.7)

где С_о — затраты на выполнение одного заказа, руб; А — потребность в заказываемом продукте в течение данного периода, шт.; С_n — цена еди­ницы продукции, хранимой на складе, руб.; i — доля от цены С_п, прихо­дящейся на затраты по хранению; S — искомая величина заказа, шт.

На рис. 4.1 представлены составляющие затрат С₃ и С_х и суммарные затраты в зависимости от размера заказа.

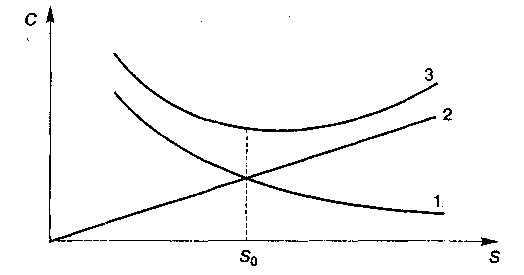
Рис. 4.1 - Зависимость затрат от размера заказа:

1 — затраты на выполнение заказа; 2 — затраты на хранение; 3 — суммарные затраты

Из рис. 4.1 видно, что затраты на выполнение заказов с увеличени­ем размера заказа уменьшаются, подчиняясь гиперболической зави­симости (кривая 1); затраты на хранение партии поставки возрастают прямо пропорционально размеру заказа (линия 2); кривая общих за­трат (кривая 3) имеет вогнутый характер, что говорит о наличии ми­нимума, соответствующего оптимальной партии S₀.

Значение оптимума S₀ совпадает с точкой пересечения зависимо­стей С₃ и С_х. Это объясняется тем, что абсцисса точки пересечения S находится из решения уравнения

(4.3) т.е. S= (4.8)

Зная S₀, нетрудно определить количество заказов:

(4.9)

минимальные суммарные затраты за рассматриваемый период:

(4.10)

время между заказами:

(4.11)

где Д — продолжительность рассматриваемого периода. Если речь идет о количестве рабочих дней в году, то Д=260дн., если о количестве недель, то Д=52 недели; в общем случае 365дн.

Формула (4.8) встречается в различных источниках под следующи­ми названиями: Уилсона (наиболее распространенное) или Вильсона, Харриса, Кампа.

Формула получена при большом количестве допущений: 1) затраты на выполнение заказа С_о, цена поставляемой продукции С_п и затраты на хранение единицы продукции в течение рассмат­риваемого периода постоянны; 2) период между заказами (поставками) постоянный; 3) заказ S_o выполняется полностью мгновенно; 4) интенсивность спроса постоянна; 5) емкость склада не ограничена; 6) рассматриваются только текущие (регулярные) запасы, другие виды запасов (страховые, подготовительные, сезонные, транзит­ные и т. д.) не учитываются.

Пример 3. Рассмотрим последовательность расчета оптимальной партии заказа. Исходные данные: потребность в заказываемом продукте (в год) А - 1000 ед.; цена единицы продукции С_п = 600 руб.; доля от цены, приходящаяся на затраты по хранению (в год), i = 0,25; затраты на выполнение одного заказа С_о = 500 руб.

Решение. По формуле (4) находим оптимальный размер заказа:

минимальные суммарные затраты на выполнение заказов и хранение продукции в течение года:

или

Определим также количество заказов и периодичность их выполнения,:

V=