Коэффициент детерминации находится по следующей формуле:
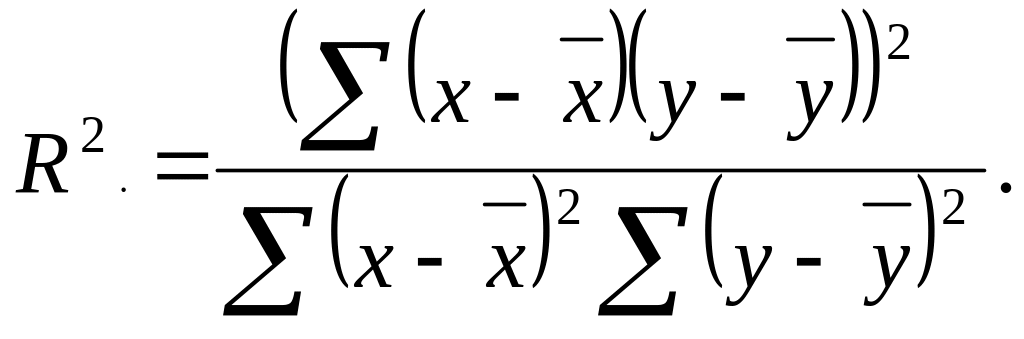
Для расчета коэффициента детерминации построим вспомогательную таблицу (табл. 2.7).
Таблица 2.7. Расчетная таблица
х |
у |
х-хср. |
(х-хср.)2 |
у-уср. |
(у-уср.)2 |
(х-хср.)( у-уср.) |
51,6 |
0,97 |
9,74333 |
94,93254 |
0,43433 |
0,18865 |
4,23185 |
50,3 |
0,85 |
8,44333 |
71,28988 |
0,31433 |
0,09881 |
2,65402 |
40,4 |
0,5 |
-1,4567 |
2,121878 |
-0,0357 |
0,00127 |
0,05195 |
50 |
0,84 |
8,14333 |
66,31388 |
0,30433 |
0,09262 |
2,47829 |
34,5 |
0,23 |
-7,3567 |
54,12054 |
-0,3057 |
0,09343 |
2,24869 |
41,4 |
0,52 |
-0,4567 |
0,208544 |
-0,0157 |
0,00025 |
0,00715 |
40,2 |
0,48 |
-1,6567 |
2,744544 |
-0,0557 |
0,0031 |
0,09222 |
41,7 |
0,5 |
-0,1567 |
0,024544 |
-0,0357 |
0,00127 |
0,00559 |
36,3 |
0,32 |
-5,5567 |
30,87654 |
-0,2157 |
0,04651 |
1,19839 |
44,6 |
0,55 |
2,74333 |
7,525878 |
0,01433 |
0,00021 |
0,03932 |
37,4 |
0,52 |
-4,4567 |
19,86188 |
-0,0157 |
0,00025 |
0,06982 |
40,2 |
0,41 |
-1,6567 |
2,744544 |
-0,1257 |
0,01579 |
0,20819 |
40,1 |
0,38 |
-1,7567 |
3,085878 |
-0,1557 |
0,02423 |
0,27345 |
44 |
0,6 |
2,14333 |
4,593878 |
0,06433 |
0,00414 |
0,13789 |
30,8 |
0,13 |
-11,057 |
122,2499 |
-0,4057 |
0,16457 |
4,48532 |
44,7 |
0,66 |
2,84333 |
8,084544 |
0,12433 |
0,01546 |
0,35352 |
44,1 |
0,53 |
2,24333 |
5,032544 |
-0,0057 |
3,2E-05 |
-0,0127 |
46,4 |
0,73 |
4,54333 |
20,64188 |
0,19433 |
0,03777 |
0,88292 |
37,2 |
0,3 |
-4,6567 |
21,68454 |
-0,2357 |
0,05554 |
1,09742 |
36,5 |
0,34 |
-5,3567 |
28,69388 |
-0,1957 |
0,03829 |
1,04812 |
39,8 |
0,43 |
-2,0567 |
4,229878 |
-0,1057 |
0,01117 |
0,21732 |
48,5 |
0,84 |
6,64333 |
44,13388 |
0,30433 |
0,09262 |
2,02179 |
36,9 |
0,4 |
-4,9567 |
24,56854 |
-0,1357 |
0,01841 |
0,67245 |
48 |
0,82 |
6,14333 |
37,74054 |
0,28433 |
0,08085 |
1,74675 |
46,7 |
0,67 |
4,84333 |
23,45788 |
0,13433 |
0,01805 |
0,65062 |
42,2 |
0,56 |
0,34333 |
0,117878 |
0,02433 |
0,00059 |
0,00835 |
35,4 |
0,29 |
-6,4567 |
41,68854 |
-0,2457 |
0,06035 |
1,58619 |
52,8 |
1,03 |
10,9433 |
119,7565 |
0,49433 |
0,24437 |
5,40965 |
41 |
0,49 |
-0,8567 |
0,733878 |
-0,0457 |
0,00209 |
0,03912 |
32 |
0,18 |
-9,8567 |
97,15388 |
-0,3557 |
0,1265 |
3,50569 |
1255,7 |
16,07 |
|
960,4137 |
|
1,53714 |
37,4094 |
41,8567 |
0,53567 |
|
|
|
|
|
Таким образом, вариация результативного признака (прибыль) на 94,8% объясняется вариацией факторного признака (цена за 1 кв.м.).
Эмпирическое корреляционное отношение равно:
,
,
где
- общая дисперсия признака У;
-
межгрупповая (факторная) дисперсия
признака У.
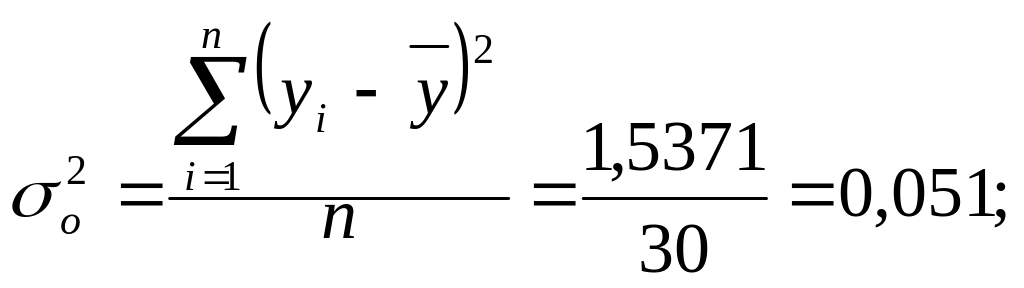
Таблица 2.8. Расчетная таблица для определения межгрупповой дисперсии
Группы |
Цена на первичном рынке жилья, тыс. руб. за кв. м. |
Прибыль,
млн. руб. ( |
Число
организаций ( |
(
- |
1 |
30,8-35,2 |
0,18 |
3 |
0,379 |
2 |
35,2-39,6 |
0,36 |
6 |
0,182 |
3 |
39,6-44 |
0,47 |
9 |
0,034 |
4 |
44-48,4 |
0,65 |
7 |
0,094 |
5 |
48,4-52,8 |
0,91 |
5 |
0,686 |
Итого |
- |
- |
30 |
1,374 |
)
)
)2
,
Эмпирический коэффициент детерминации:
То есть, 89,4% вариации результативного признака У обусловлено вариацией признака-фактора Х, а 10,6% - влиянием прочих неучтенных факторов.
Эмпирическое
корреляционное отношение
оценивает тесноту связи между факторным
и результативным признаком. Для
качественной оценки тесноты связи на
основании
служит шкала Чэддэка.
Таблица 2.9. Шкала Чэддэка
|
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
Характеристика силы связи |
слабая |
умеренная |
заметная |
тесная |
весьма тесная |
Таким образом, связь между факторным и результативным признаком является весьма тесной.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,997 определите:
1. Ошибку выборки средней цены за кв. м. на первичном рынке жилья и границы, в которых она будет находиться для генеральной совокупности строительных организаций-застройщиков.
2. Ошибку выборки доли организаций с ценой на первичном рынке жилья 44 тыс. руб. за кв. м. и более и границы, в которых будет находиться генеральная доля.
Решение
При заданной вероятности (0,997) коэффициент доверия t, согласно таблице значений интегральной функции Лапласа, равен 2,97, n (численность выборки) равно 30, а так как выборка 20%-ая, то N (объем генеральной совокупности) равен 150 органиазций.
Ошибка выборки определяется по формуле:
Границы, в которых будет находиться средняя цена за кв. м. на первичном рынке жилья для организаций генеральной совокупности:
Выборочная доля w, или частность, определяется отношени ем числа единиц, обладающих изучаемым признаком m, к об щему числу единиц выборочной совокупности n:
w = m/n.
Доля организаций с ценой на первичном рынке жилья 44 тыс. руб. за кв. м. и более:
w = 12 / 30 = 0,4.
Предельная ошибка для доли при бесповторном случайном и механическом отборе рассчитывают по следующей формуле:
Границы генеральной доли рассчитываются по формуле:
Задание 4
Имеются данные об объеме построенного жилья в регионе за ряд лет.
Таблица 2.10. Исходные данные
Год |
Число построенных квартир, тыс. ед. |
1 |
529 |
2 |
589 |
3 |
677 |
4 |
649 |
5 |
680 |
6 |
753 |
7 |
792 |
Определите:
Базисные и цепные абсолютные приросты, темпы роста и прироста построенного жилья (результаты расчетов представьте в таблице).
Средний уровень ряда, среднегодовой абсолютный прирост, среднегодовые темпы роста и прироста построенного жилья.
Осуществите прогноз строительства жилья на 8-ой год при условии сохранения среднегодового темпа роста строительства.
Сделайте выводы.