6 Задачі керування

Приведена в попередньому прикладі керуюча структура відноситься до одної із простих; вона зводиться до перебирання правил, поки одне із них не спрацює, і повторення циклу з самого початку. У більшості реальних системах задача керування значно складніша.

В системах штучного інтелекту задачі керування звичайно представляються за допомогою концепції так званого “пошуку в просторі станів”. При рішенні задач на основі знань, як правило, не існує єдиного методу досягнення мети. У зв’язку з цим виникає необхідність в спробувані декількох можливих шляхів і з’являється бажання оцінити на кожному етапі ймовірність досягнення кінцевої мети.

Керуюча структура систем, які вирішують задачі, визначає загальну стратегію вибору таких шляхів. Вона навіть може “зайняти” у логіці термін “форма” і “вести розмову” про “форму” рішення задач, що прийнята до деякої конкретної предметної області.

Підхід “пошук в просторі станів” сформувався в результаті спроб автоматизації ігор. В більшості ігор має кінцеву кількість позицій (чи “станів”), які можуть бути досягненні при використані фіксованого набору правил, що визначають гру.

Тому (у всякому випадку в теорії) існує можливість опису послідовності гри шляхом перерахування всіх позицій, які можуть бути досягненні із заданого початкового стану.

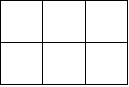
Ця множина позицій може бути представлена у вигляді дерева, яке простирається з кореня, що відповідає початковому стану гри, до заключних позицій, досягнутих в кінці гри. На рис.22 приведені всі можливі позиції для чотирьох перших ходів в простій грі “хрестики-нулики”.

Для тих, хто не знайомий з цією грою, порснемо її правила.

Правила гри:

Є два знаки (фішки) 0 і Х і позиції, що задані матрицею 3Х3.

Два гравця (один грає фішками 0, інший – фішками Х) беруть почергово по відповідній фішці і розміщують їх у вільні комірки матриці. Мета гри – встановити підряд (в лінію) 3 однакові фішки; гравець, що перший досягне такого положення для своїх фішок, виграв.

7

х х

х

0 0 х х

х х 0 0

х х х х

0 0

0 0

0 0 0 0

х х х х х

х х х

х х х х х

0 х 0 0 0

х х

0 0 0 х х 0 х х

0 х х х 0 0 0 0 0

х 0 х 0 х х х

Рис.22. Чотири хода “хрестики-нулики”

В рамках описаного вище представлення “простору станів” положення фішок (стани), відповідні успішній грі, можна розгледіти серед заключних позицій дерева. Виграшні послідовності ходів можуть бути виявлені в результаті прокладення шляху від вихідного стану до виграшного.

При представлені простору задачі через стани знайдена ефективність пошуку рішення із застосуванням правил чи операторів (відповідних частин правил, що виражають “дію”), які запускаються при досягнені даного стану гри і здійснюють перехід до нового стану.

8

В грі “хрестики-нулики” існує тільки один тривіальний оператор – встановлення фішки (0 чи Х) в порожній квадрат матриці. Але в інших іграх операторів може бути декілька. Наприклад, в шахматах предписані для кожної із фігур ходи можна розглядати як оператори, що перетворюють картину шахматної позиції і таким чином пересуваючи гру від одного стану в інший.

Залишається ще одна проблема. В більш складній грі потрібно забезпечити деякі засоби для рішення питання про те, яке правило чи оператор необхідно застосувати для кожного із станів при пересуві до мети. Загальна стратегія керування подібним вибором рішень відома як керуюча структура.

Простіша стратегія звичайно має повний перебір дерева преостору станів для пошуку прийнятого ходу. Напрямок, по якому досягається той чи інший стан, часто має велике значення для систем, що маніпулюють значеннями.

В зображеній на рис.22 діаграмі станів наша вихідна позиція знаходиться у верхній частині малюнка, а кінцева мета – внизу. (Можливо більш одного вихідного стану в деяких просторах станів). КІоли такі діаграми застосовуються в системах, побудованих на основі знань, їх звичайно зображують пр-іншому : мету розміщують наверху, а вихідну позицію – внизу. Це пов’язано з тим, що увага концентрується на цілях (наприклад, ми хочимо досягнути контретної мети – рішення нашої задачі). В таких випадках напрямок пошуку тим не менш визначається виходячи із початкового стану. Наприклад, при зворотньому напрямку пошуку пересування відбувається від мети до початкового стану, а при прямому – від початкового стану до мети. Застосовуєтьсята інше позначення напрямку пошуку – “зверху вниз” чи “знизу вверх”. В цьому випадку “зверху вниз” означає пошук від мети до початкового стану, а “снизу вверх” – від початкового стану до мети.

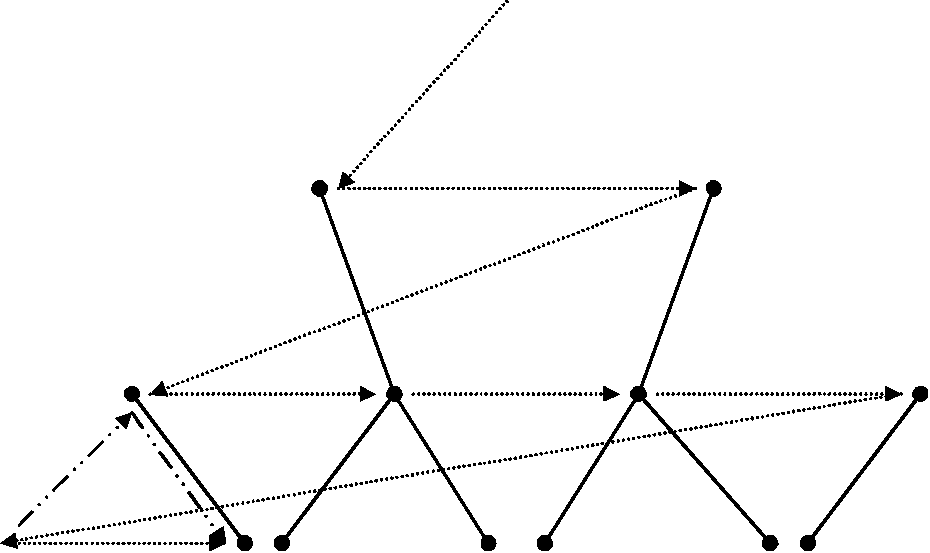
Існує більш загальний підхід до вибору напрямку пошуку в просторі станів. Незалежно від орієнтації пошуку дерево станів, що починається від заданої мети чи початкового стану, може бути переглянуте “спочатку вглиб” чи “спочатку вшир”. При пошуку “спочатку вглиб” дерево переглядається із заданого стану на всю глибину до вичерпання послідовності “наслідуваних” станів на цьому шляху. Потім переглядаються альтернативні шляхи, які ведуть в глиб дерева. При пошуку “спочатку вшир” відбувається породження всіх можливих альтернати на заданому рівні, потім всіх альтернатив на наступному рівні тощо. В результаті пошук проводиться “в ширину” дерева. Рис.23 ілюструє ці два варіанти.

9

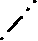
“спочатку вглиб” “спочатку вшир”

Рис.23. Пошук “спочатку вглиб” і “спочатку вшир”

Але із досягенням мети (чи із рішенням задачі) завдяки засобам вичерпного пошуку (повного перебору) в просторі станів пов’язана достатньо серйозна проблема. Це може викликати здивування, але навіть в такій простій грі, як “хрестики-нулики”, існує 362 880 (9!) можливих позицій. Завдяки симетрії деяких з них цю цифру можна скоротити приблизно до 60 000. В таких складних іграх, як шахмати, було би неможливо провести пошук по всьому дереву гри. Хугеланд підрахував, що перегляд наперед на 5 ходів дає квадріліон (1015) комбінацій, а 40 ходів ( в средньому за гру) дають 10120 комбінацій. При цьому він відмітив, що з моменту зародження Всесвіту пройшло менше 1080 секунд! На кожному кроці кількість варіантів вибору множить загальне число комбінацій. Цей процес, отримавший назву “комбінаторного вибуху”, виключає застосування стратегії пошуку повним перебиранням для більшості реальних ігор, а також і для більшості систем на основі знань.

Очевидно, що із-за великої кількості позицій навіть в простій грі, такій, як “хрестики-нулики”, ні один гравець не проводить пошук наступного ходу простим перебиранням. Те, що гравець буде робити, є застосування визначених стратегічних правил для виявлення того, які з зодів забезпечують найбільшу ймовірність успіху. В багатьох випадках це приводить до значного скорочення числа переглянутих позицій. Але дуже рідко вдається встановити з абсолютною визначеністю, які ходи повинні розглядатися. Деякі ходи на перший погляд представляються безуспішними, але вони можуть оказатися

10

ефективними в якості особливого контрходу. В більшості ігор ( і взагалі ситуацій при обробці знань) часто неможливо знайти правида, що гарантують успіх. Разом з тим часто вдається встановити правила, які забезпечують збільшення ймовірності успіху. Такі правила називають “еврістичними”, а пошук, при проведені якого вони застосовуються, називається еврістичним пошуком. Для еврістичного правила необхідна інформація про його ефективність. Ця інформація визначається за деякими “оціночними функціями”. В грі “хрестики-нулики” використовується проста оціночна функція. Деяке значення (число) прсваюється кожному наступному можливому ходу. Чим воно вище, тим ліпше для одного гравця. Чим воно нище, тим ліпше для іншого. Ця процедура називається MINIMAX. Проілюструємо застосування процедури MINIMAX при грі в “хрестики-нуликиФ” :

х

о

1 2 3 4

х х х х х

о х о о о

х х

Max (х) 4 4 4 4

Min (о) -4 -4 -3 -5

0 0 1 -1

Рис.24. Застосування оціночної функції в грі “хрестики-нулики”

Припустимо, що є два гравця – МАХ (що грає фішками Х) і MIN (що грає фішками 0). Значення оцінки для доступних їм ходів можуть бути отримані шляхом підрахунку всіх ліній, відкритих для кожного із гравців, а потім різниця одного числа із іншого. Застосувавши до позиції, приведеної на рис.24, МАХ повинен зробити вибір серед ходів 1, 2, 3 І 4. Вони відповідно отримують оцінки 0, 0, 1, і –1. МАХ вибирає хід 3, так як він отримав найвищу оцінку для цього раунда.

В грі в “хрестики-нулики” прийнята конструкція єдиної оціночної функції, яка надійно прокладує шлях до оптимальному рішеню. Але часто дуже тяжко, якщо не неможливо, знайти таку функцію для багатьох задач

11

реального світу. Одна із складностей, про яку згадувалось вище прийнятої до шахматів, є в тому, що якийсь із позицій гри, можливо, необхідно зробити хід, що здається менш вдачним, з тим, щоби пізніше досягнути перевагу. Багато зусиль в роботі, пов’язаної з керуючими структурами в області штучного інтелекту, було затрачено при спробах справитися з подібними складними ситуаціями. Дві універсальні стратегії, застосовані в експертних системах, запропоновують наступне :

Організувати простір задачі таким чином, щоби в початку пошуку рішення можна було сказати, наскільки воно буде успішним; в цьому випадку може бути виключена необхідність перебору всієї множини шляхів пошуку;

Побудувати простір задачі у вигляді ряду підпросторів з мінімальними взаємозв’язками чи без взаємозв’язків між ними. В результаті цього кожна із підзадач може бути вирішена незалежно від рішення наступних задач.

Обсудження цих стратегій буде продовжене при розгляді відповідних експертних систем в наступних розділах, так як застосованість тих чи інших стратегій в дуже сильному ступені залежить від структури знань предметної області, і, значить, ліпше всього розглядати їх в контексі конкретних задач. Процес конструювання системи на основі знань можна трактувати як встановлення тих властивостей предметної області, які дають можливість побудувати задачу таким чином, щоби звести до мінімуму обчислювану роботу.