4. Проектный расчет цилиндрической зубчатой передачи редуктора

4.1. Определим главный параметр – межосевое расстояние

, (24)

где К_а – вспомогательный коэффициент, для косозубых передач, К_а = 43,

(для прямозубых - К_а = 49,5);

– коэффициент ширины венца колеса, равный 0,28…0,36, для шестерни, расположенной симметрично относительно опор для рассматриваемого варианта;

U – передаточное число редуктора, в нашем случае U =5 (см. раздел 1 «Кинематический расчет привода»);

Т₂ – крутящий момент на тихоходном валу редуктора, кН м, для рассматриваемого варианта Т₂=Т₃=0,307 кН м (см. раздел 1 «Кинематический расчет привода»);

[н] - допускаемое контактное напряжение колеса с менее прочным зубом или среднее допускаемое контактное напряжение, Н/мм², [н] = 637 МПа (см. раздел 2 п. 2 «Определение допускаемых контактных напряжений для зубьев шестерни и колеса»);

Кн – коэффициент неравномерности нагрузки по длине зубьев.

Зная значение коэффициента ψ_а определяем значение коэффициента _вd на зависимости : _вd = 0,5_а (U 1), а затем по графику рис. 4 , в зависимости от расположения колес относительно опор и твердости поверхности зубьев выбираем значение коэффициента Кн.

_вd= 0,5 0,3(5+1)=0,9 ,знак «+» берем в формуле, т.к. имеет место внешнее зацепление пар зубьев.

По рис. 4, имеем, что Кн = 1.

Подставим все известные величины в формулу (24) и рассчитаем численное значение межосевое расстояние а_:

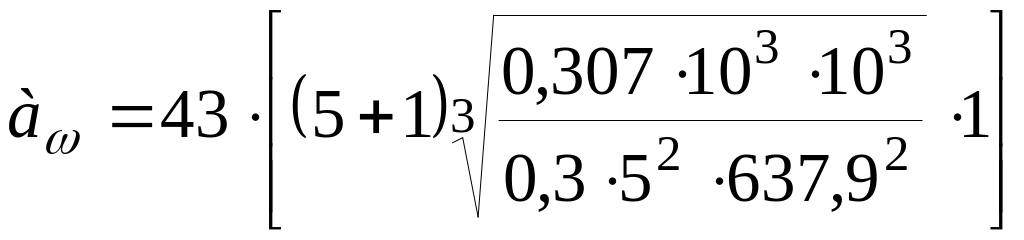= 120,1 (мм)

полученное значение межосевое расстояние а_ округляем до ближайшего стандартного:

стандартные межосевые расстояния :

1-й ряд – 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400…

2-й ряд – 140, 180, 225, 280, 355, 450…

Получаем стандартное ближайшее значение межосевого расстояния а_ = 120 мм.

4.2. Определим модуль зацепления m, мм :

, (25)

где Кm - вспомогательный коэффициент, для косозубых передач, Кm=5,8 (для прямозубых Кm=6,8);

d₂ = 2 а_  U / (U 1) – делительный диаметр колеса, мм;

подставив известные величины имеем, что :

d₂ = 2 а_  U / (U 1) = 2  120  5 / (5+1) = 200 (мм);

b₂ = _а  а_w – ширина венца колеса, мм, подставив численные значения известных величин составляющих формулу получаем:

b₂ = 0,3  120= 36 (мм) ;

[_F] - допускаемое напряжение изгиба материала колеса с менее прочным зубом, МПа (см. раздел 2 п.3 «Определение допускаемых напряжений изгиба для зубьев шестерни [] F₁ и колеса []F₂) ;

[_F] = [_F2] = 294 МПа.

Т₂ – крутящий момент на тихоходном валу редуктора, КН  м, для нашего случая

Т₂ = Т₃ = 0,307 кН  м (см. раздел 1 «Кинематический расчет привода»).

Подставим известные величины в формулу (25) получим численное значение для модуля зацепления :

= 1,68 мм

полученное значение модуля округляем до ближайшего стандартного в большую сторону из ряда чисел: m, мм

1-й ряд : 1,0 ; 1,5 ; 2 ; 2,5 ; 3 ; 4 ; 5 ; 6 ; 8 ; 10

2-й ряд : 1,25 ; 1,75 ; 2,25 ; 2,75 ; 3,5 ; 4,5 ; 5,5 ; 7 ; 9

Принимаем m=2 мм.

4.3. Определим угол наклона зубьев _min для косозубой передачи редуктора:

sin , (26)

где m- модуль зацепления;

– ширина венца зубчатого колеса.

По формуле (26) получаем, что :

sin 0,1944

В косозубых передачах угол наклона зубьев принимают β= 8…16.

4.4. Определим суммарное число зубьев шестерни и колеса :

Z_=Z₁+Z₂=2 а_cos_min/m (27)

получаем :

Z_= 2  120  cos 11,21/2 = 117,7.

Полученное значение Z_ округляем в меньшую сторону до целого числа, имеем: Z_= 117.

4.5. Уточним действительную величину угла наклона зубьев,

cos =(Z_m/2 а_)) (28)

получаем :

β=arc cos(117  2/(2  120))  12,84.

4.6. Определим число зубьев шестерни :

. (29)

Подставив в формулу (29) определим ранее величины получаем, что:

= 19,5.

Округлим полученное значение до ближайшего целого получим Z₁=20, что соответствует условию уменьшения шума и отсутствия подрезания зубьев Z₁  18

4.7. Определим число зубьев колеса :

Z₂=Z_-Z₁. (30)

Имеем : Z₂=117 - 20=97.

4.8. Определим фактическое передаточное число U_ф и проверим его отклонение ΔU от заданного U ( получено 8 разделе 1 «Кинематический расчет привода»):

. (31)

Подставив известные значения числа зубьев шестерни и колеса имеем, что

= 4,85.

, условие выполняется.

4.9. Определим фактическое межосевое расстояние :

а_ = (Z₁ + Z₂)m/ (2cos ) = (20+97)2∕(2 cos  12,84)=120 мм.

4.10. Определим основные геометрические параметры передачи :

а) Диаметры делительных окружностей шестерни и колеса :

d₁=mZ₁/cos; (33)

d₂ = m Z₂ / cos

по формуле (33) имеем :

d₁ = m Z₁ / cos = 2  20/cos 12,84= 41,03 (мм) ;

d₂ = m Z₂ / cos= 2  97/ cos  12,84= 198,98 (мм) ;

4.10 Определим диаметры вершин d_а и впадин d_f шестерни и колеса:

d_а1 = d₁ +2 m ;

d_а2 = d₂ + 2 m ; (34)

d_f1= d₁ – 2,4 m ;

d_f2 = d₂ – 2,4 m .

Подставив известные величины в формулу (34) получаем, что :

d_а1 = d₁ +2 m = 41,03 + 2 2 = 45,03 (мм)

d_а2 = d₂ + 2 m = 198,98 + 2 2= 202,98 (мм)

d_f1= d₁ – 2,4 m = 41,03 – 2,4 2 = 36,23 (мм)

d_f2 = d₂ – 2,4 m = 198,98 – 2,4 2 = 194,18 (мм)