За якими критеріями вибирається регресія, що найкраще з-поміж інших описує емпіричні дані?
Опишіть алгоритм побудови довірчих інтервалів із заданою надійністю для параметрів теоретичної множинної лінійної регресії.
Розрахунок довірчих інтервалів
для оцінок параметрів
,
та
із заданою надійністю
Довірчі
інтервали для коефіцієнтів регресії
визначаються за формулою:
,
де
– задана надійність;
– табличне значення.
Отже,
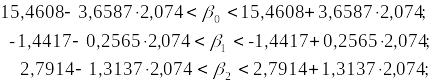
або
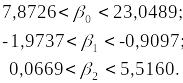
На основі
побудованої залежності можна зробити
висновок, що ціна автомобіля, який міг
би мати технічні характеристики, рівні
середнім значенням
та
,
дорівнювала б завдяки
середньому значенню залежної змінної
–
=13,024
тис.дол. Збільшення віку автомобіля на
один рік зменшує ціну на 1,4417 тис.дол., а
збільшення об’єму двигуна на 1дм3
призводить до збільшення ціни на 2,7914
тис.дол. Фактори, включені в модель,
пояснюють “поведінку” ціни на 67,4%.
Звичайно, це можна пояснити тим, що на
формування ціни на автомобіль мають
вплив також інші фактори (престиж марки,
тип двигуна, оснащення салону, колір
тощо), які в даному прикладі не розглядались.
Условній и безусловній прогноз
Условный прогноз - прогноз, который осуществляется, исходя из
постановки задачи, структура которой может быть выражена условием: «Если A
примет значение А1, то B примет значение В1». То есть, такой прогноз
позволяет выяснить возможные состояния объекта при тех или иных условиях.
Безусловный прогноз - прогноз, который определяет будущее объекта без
учета каких-либо условий, например: «В примет значение В1». Впрочем, можно
согласиться с мнением о том, что безусловный прогноз - это разновидность
условного прогноза - его действительно можно сформулировать следующим
образом: «Если ничего не будет меняться, то В примет значение В1».