1. Яким чином здійснюється перевірка статистичної значущості параметрів та перевірка загальної якості множинної регресії?

Обчислимо критерій.

Для визначення критеріїв необхідно знайти матрицю , яка є оберненою до матриці .

Для знаходження оберненої матриці використовується _{функція} MS Excel «МОБР». Для використання даної функції слід виконати наступні кроки:

Крок 1: Виділити комірку, яка буде лівим верхнім кутом результуючої матриці, наприклад G33.

_{Крок 2:} У виділену комірку записати формулу: , де аргументами є діапазон кореляційної матриці _.

Крок 3: Виділити весь діапазон, де буде розміщена обернена матриці (G33:І35).

_Крок 4: Натиснути функціональну клавішу F2, а потім клавіші Ctrl+Shift+Enter. В результаті отримаємо обернену матрицю _:

Безпосередньо критерій обчислюється за формулою:

, (7)

де – діагональний елемент матриці .

;

;

.

Обчислені критерії порівнюються з табличним значенням , коли є ступенів свободи та при рівні значущості .

У розглядуваному випадку , , . Це означає, що кожна з пояснюючих змінних мультиколінеарна з іншими.

. Визначимо критерій.

Ці критерії застосовуються для визначення мультиколінеарності двох пояснюючих змінних і обчислюються за формулою:

. (9)

;

;

.

Обчислені критерії порівнюються з табличним значенням , коли маємо ступенів свободи та при рівні значущості .

Оскільки , то продуктивність праці та фондовіддача є відповідно мультиколінеарними між собою;

, тому відповідно продуктивність праці та питомі інвестиції є мультиколінеарними між собою;

, тому продуктивність праці та питомі інвестиції не є мультиколінеарними між собою.

Як визначаються дисперсія залишків, загальна дисперсія і дисперсія регресії? Який між ними зв’язок

. Дисперсійний аналіз моделі та обчислення коефіцієнта множинної детермінації

Проведемо дисперсійний аналіз побудованої моделі. Відомо, що

.

Можна довести, що й для дисперсій цих змінних виконується рівність:

.

Розрахунки табл. 4.2 підтверджують цей висновок. Користуючись розрахунками, наведеними в табл. 4.2, обчислимо коефіцієнт множинної детермінації:

;

.

3. Перевірка статистичної значущості коефіцієнта множинної детермінації за критерієм Фішера

Для перевірки статистичної значущості впливу регресорів на залежну змінну моделі використовуємо статистичний критерій Фішера:

;

при рівні значущості =0,05 та ступенях свободи k₁=m=2 i k₂=n-m-1=22 по таблиці розподілу Фішера знаходимо =3,44.

Обчислимо спостережене значення критерію за формулою:

.

Критерій Фішера має правобічну критичну область із критичною точкою робимо статистичний висновок:

оскільки > , то статистична гіпотеза відхиляється, отже всі регресори мають вплив на залежну змінну.

4. Визначення дисперсій оцінок параметрів та їх стандартних помилок

Знайдемо тепер незміщену оцінку для дисперсії залишків :

;

.

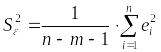Оцінка якості моделі

Модель вважається гарною зі статистичної точки зору, якщо вона адекватна і достатньо точна.

1. Для перевірки адекватності моделі реальному явищу досліджується ряд залишків, тобто розбіжностей рівнів, розрахованих по моделі, та фактичних спостережень.

а) Перевірка рівності математичного очікування рівнів ряду залишків нулю здійснюється в ході перевірки відповідної нульової гіпотези . З цією метою будується t-статистика:

(5.17)

де  – середнє арифметичне значення рівнів ряду залишків;

S – середньоквадратичне відхилення для цієї послідовності, розраховане для малої вибірки.

В подальшому дане розраховане значення порівнюють з табличним і роблять висновок про прийняття або відхилення гіпотези.

б) Перевірка умови випадковості виникнення окремих відхилень від тренду.

в) Перевірка умови незалежності, або наявності автокорреляції у відхиленнях від моделі росту (буде розглянуто пізніше).

г) Відповідність ряду залишків нормальному закону розподілу.

2. Оцінка точності моделі. В статистичному аналізі широко відомо велика кількість характеристик точності. Найбільш часто, окрім середньоквадратичного відхилення, використовують:

• максимальна за абсолютною величиною похибка

; (5.18)

• відносна максимальна похибка

; (5.19)

• середня по модулю похибка

; (5.20)

• середня по модулю відносна похибка

. (5.21)

Кращою за точністю вважається та модель, у якої всі перелічені характеристики мають меншу величину.