1. Назвіть два класи нелінійних регресій.

2. Наведіть приклади регресій, нелінійних відносно пояснюючих змінних, однак лінійні по параметрам, що оцінюються.

3. Наведіть приклади регресій, нелінійних по параметрам, що оцінюються.

Розрізняють два класи нелінійних регресій:

1) нелінійні відносно пояснюючих змінних, однак лінійні по параметрам, що оцінюються;

2) нелінійні по параметрам, що оцінюються.

Клас регресій нелінійних відносно пояснюючих змінних, однак лінійних по параметрам, що оцінюються, включає рівняння, в яких залежна змінна лінійно пов’язана з параметрами. Приклад таких регресій можуть слугувати:

• поліноми різних ступенів

; (5.1)

• рівностороння гіпербола

. (5.2)

При оцінці параметрів регресії, нелінійних по пояснюючим змінним, використовується метод заміни змінних. Суть його полягає в заміні нелінійних пояснюючих змінних новими лінійними змінними, в результаті чого нелінійна регресія зводиться до лінійної. До нової, перетвореної регресії може бути застосований звичайний МНК.

Наприклад, у випадку поліноміальної моделі з декількома пояснюючими змінними

(5.3)

заміна , , , ... призводить до лінійної регресійної моделі.

До класу регресій, нелінійних по параметрам, що оцінюються, відносяться рівняння, в яких залежна змінна нелінійно пов’язана з параметрами. Прикладом таких регресій є функції:

• степенева: ;

• показникові: ;

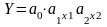• експоненціальні: .

4. Яка нелінійна модель називається внутрішньо лінійною?

5. Яким чином здійснюється параметризація внутрішньо нелінійних рівнянь регресії?

Якщо нелінійна модель внутрішньо лінійна, то вона за допомогою відповідних перетворень може бути приведена до лінійного виду (наприклад, логарифмуванням). Якщо ж нелінійна функція внутрішньо нелінійна, то вона не може бути зведена до лінійної функції і для оцінки її параметрів використовують ітеративні процедури, успішність яких залежить від виду рівняння та особливостей ітеративного підходу, що застосовується.

Прикладом регресії, що є внутрішньо лінійної є регресія попиту (Y) від загального доходу (z) та ціни цього товару (p):

. (5.4)

Подібні залежності між показником Y та m факторами Z₁, Z₂, ..., Z_m записуються у вигляді

(5.5)

і за допомогою логарифмічного перетворення

(5.6)

зводяться до лінійної по параметрам регресії. Визначення

, , , ..., (5.7)

призводять до лінійної регресійної моделі

. (5.8)

Після оцінювання лінійної моделі (5.8) за допомогою відношень (5.7) можна знайти оцінену регресію для моделі (5.5):

. (5.9)

Моделі виду (5.5) отримали широке розповсюдження при економетричному моделюванні. Це пов’язано з тим, що параметри такої моделі мають змістовну економічну інтерпретацію. З (5.5) випливає, що

, (5.10)

тобто параметр a_i представляє собою коефіцієнт еластичності показника Y по змінній x_i.

Для моделей виду

(5.11)

також використовується логарифмічне перетворення, оскільки визначення , , , ..., приводять їх до лінійної регресії (5.8).

Вибір аналітичної форми дослідження моделі може здійснюватися на основі апріорної інформації про залежність та на основі графіків розкиду емпіричних точок.