21.1. Основные физические свойства влажного газа

Смесь сухого газа с парами жидкости называется влажным газом. Влажный газ характеризуют следующие параметры: температура; давление; плотность; относительная и абсолютная влажность; влагосодержание; теплоемкость; энтальпия.

Влажный воздух, который наиболее часто используют в качестве сушильного агента, можно считать при небольших давлениях и положительных температурах бинарной смесью идеальных газов: сухого воздуха и водяного пара. В соответствии с законом Дальто- на давление идеальной газовой смеси является суммой парциальных давлений ее компонентов:

Р = р_с.г. + р_п, (21.5)

где Р - давление, при котором находится парогазовая смесь; р_с.г., р_п. – парциальные давления сухого газа и водяного пара соответственно.

Пар называют свободным или перегретым при температуре t и давлении Р, если он не конденсируется в этих условиях. Максимально возможное содержание пара в газе, выше которого наблюдается конденсация, соответствует условиям насыщения при определенной температуре t и парциальном давлении р_н.п.

Различают абсолютную, относительную влажности и влаго-содержание влажного воздуха.

Абсолютная влажность - это масса водяного пара в единице объема влажного воздуха. Поскольку пар как компонент бинарной газовой смеси занимает весь объем влажного газа, понятие абсолютной влажности совпадает с понятием плотности пара ρ_п (в кг/м³) при температуре t и парциальном давлении р_п.

Относительная влажность (φ) - это отношение количества паров жидкости в газе к максимально возможному при данных температуре и общем давлении или (что то же) отношение плотности пара р_п при данных условиях к плотности насыщенного пара ρ_и.п при тех же условиях:

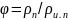. (21.6.)

По уравнению состояния идеального газа для пара в свободном и насыщенном состояниях имеем

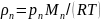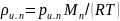, ( 21.7)

Подстановка зависимости (21.7) в уравнение (21.6) приводит к следующему выражению:

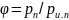(21.8)

Под влагосодержанием х понимают количество пара жидкости (в кг), приходящегося на 1 кг абсолютно сухого газа:

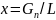, (21.9)

где 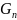- масса (массовый расход) пара, кг (кг/с); L масса (массовый расход) абсолютно сухого газа, кг (кг/с).

Выразим величины и L через уравнение состояния идеального газа:

, .

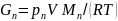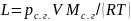Тогда соотношение (21.9) преобразуется к виду

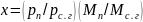, (21.10)

Учитывая, что 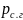= Р — р_п, имеем

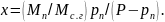(21.11)

Так как 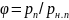, получим:

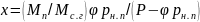(21.12)

Для системы водяной пар-воздух уравнение (21.12) преобразуется (при М_п = 18 кг/моль и М_{с г} = 29 кг/моль) к виду

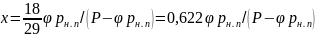. (21.13)

Удельная теплоемкость влажного газа принимается аддитивной величиной теплоемкостей сухого газа и пара. При этом различают Удельную теплоемкость с_см, отнесенную к 1 кг парогазовой смеси:

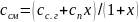. (21.14)

и удельную теплоемкость влажного газа c, отнесенному к 1 кг сухого воздуха (эту величину обычно используют при расчетах):

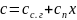(21.15)

Здесь с_с.г - удельная теплоемкость сухого газа, Дж/(кг*К); с_п- удельная теплоемкость пара, Дж/(кг*К).

Удельную энтальпию (Н) парогазовой смеси (в Дж/кг) выражают также по правилу аддитивности как сумму удельных энтальпий сухого газа Н_с.г и пара Н_п:

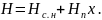(21.16)

Удельную энтальпию свободного (перегретого) пара опреде­ляют по следующему выражению:

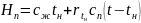, (21.17)

где с_ж - теплоемкость конденсата пара; t_н- температура насыщения, соответствую­щая парциальному давлению пара в парогазовой смеси; 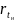- удельная теплота парообразования при температуре насыщения; t_н - температура свободного (перегретого) пара.

Удельная энтальпия Н_н.п пара при температуре насыщения находится так:

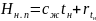. (21.18)

Для изолированной системы справедливо также равенство

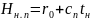. (21.19)

где 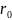- удельная теплота парообразования при 0°С.

С учетом выражений (21.18) и (21.19) уравнение (21.16) будет иметь следующий вид:

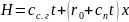. (21.20)

Отметим, что уравнение (21.20) является базовым для построе­ния диаграмм энтальпия-влагосодержание (например, диаграмм: Рамзина-Молье для влажного воздуха).

При расчетах сушильных устройств требуется знать объемные значения потоков V при соответствующих параметрах парогазовой смеси, которые определяют из выражения

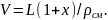(21.21)

При этом плотность парогазовой смеси ρ_см можно представить как сумму концентраций (плотностей) сухого газа и пара жидкости, находящихся в данном объеме (при условии его постоянства):

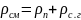. (21.22)

С учетом уравнения состояния идеального газа имеем

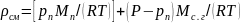. (21.23)

Путем несложных преобразований с учетом (21.11) можно по­казать, что уравнение (21.23) приводится к виду

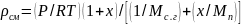(21.24)

Формула (21.24) удобна для расчетов плотности парогазовой смеси. Согласно этому выражению при постоянстве общего давле­ния плотность смеси уменьшается при увеличении температуры и влагосодержания.

Отметим, что давление насыщенного пара при атмосферном давлении Р парогазовой смеси зависит только от температуры и находится по таблицам равновесия пар – жидкость.