Список літератури

1. Кабушкин Н.И. Основы менеджмента. – Минск: Экономпресс, 1998

2. Економіка та організація виробництва: Підручник / за ред. В.Г.Герасимчука, А.Е.Розенплентера. - К.: Знання, 2007. - 678 с.

3. Сероштан М.В., Михеєва Е.Н. Качество непродовольственных товаров. Учебное пособие для Вузов.- М.: Издательский дом „Дашков и К”, 2000.-164 с.

4. Теорія і практика маркетингу в Україні: Монографія / А.Ф.Павленко, А.В.Войчак, В.Я.Кардаш, В.П.Пилипчук та ін.; за наук. ред. д-ра екон. наук, проф., акад.. АПН України А.Ф. Павленка.- К.:КНЕУ, 2005.-584 с.

5. Смирнов А.Н. Основы идентификации и сертификации продукции: Учебное пособие для вузов – Донецк, ДонНТУ, 1999. – 150 с.

6. Беквит Г. Продавая незримое: Руководство по современному маркетингу услуг/ пер. с англ.- М.: АльпинаБизнес Букс, 2004.- 272 с.

7. Мескон М., Хедоури Ф. Основы менеджмента/ пер. с англ. -М.: Дело, 1999. - 800с.

8. Надтока Т.Б., Виноградов А.Г. Функционально-стоимостный анализ: Уч. пособие.- Донецк: ДонНТУ, 2007.- 132 с.

9. Фатхутдинов Р.А. Производственный менеджмент: Учебник для вузов. – 3-е изд., перераб. и доп. - М.: Изд.-торговая корпорація „Дашков и К”, 2005. – 472 с.

10. Економика промышленного предприятия / Под ред. Евдокимова Ф.И., Надтоки Т.Б. – Донецк: ДРУК-ИНФО, 2005. – 434 с.

11. Маркетинг і комп’ютер / За ред. Євдокимова Ф.І., Тарас’євої Л.В. - Донецк: ДРУК-ИНФО, 2006. – 540 с.

12. Пасічник В.Г., Акіліна О.В. Конкурентоспроможність фірми: навчальний посібник.- Київ: Центр навчальної літератури, 2005.-112 с.

13. Резникова Н. Маркетинг в телекоммуникациях, 1-е издание, — М.: Эко-трендз, 1998.

14. Лаврененко В.В. та ін. Організаційний розвиток підприємства. – К.: КНЕУ, 2005. – 197 с.

15. Перерва П.Г., Гаврись О.М., Погорелов Н.І. Економіка і маркетинг виробничо-підприємницької діяльності. – Харків, НТУ, ХПУ. -2004. – 640 с.

Додатки

Додаток А

Приклад до практичного заняття 2

“Побудова і розрахунок параметрів

Сітьових графіків. Оптимізація сітьових графіків”

Основні визначення

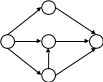
Сітьовий графік – графічне зображення досліджуваного комплексу робіт, що характеризує їх логічний взаємозв’язок та тривалість.

Основними елементами сітьового графіка є:

• події;

• роботи.

Подія – результат будь-якої роботи, комплексу робіт, який можна зафіксувати. Подія, в яку не входить жодна робота називають початковою подією. Подія, з якої не виходить жодної роботи, називають кінцевою подією.

Робота – процес, що призводить до певної події.

Інколи робота відображає лише логічний зв'язок подій або очікування. У такому разі роботу називають фіктивною, а на графіку її позначають пунктиром.

Критичний шлях – той проміжок часу, найменший з початку відліку, за який звершиться кінцева подія.

Основні формули

Очікувана тривалість роботи:

для двох оцінок ( , ) : ;

для трьох оцінок ( , , ) : ,

де - найбільш вірогідна тривалість даної роботи.

Дисперсія:

для двох оцінок ( , ) : ;

для трьох оцінок ( , , ) : .

Ранній термін події: найдовший шлях від початкової 0 події до тієї, що розглядається

Пізній термін події: найдовший шлях від кінцевої події до тієї, що розглядається

Ранній термін початку роботи:

Ранній термін закінчення роботи:

Пізній термін закінчення роботи:

Пізній термін початку роботи:

Резерв часу події:

- максимальний проміжок часу, на який може бути відстрочено звершення події без зміни тривалості критичного шляху.

Повний резерв часу роботи:

- час, на який можна збільшити тривалість роботи, не змінюючи тривалості критичного шляху.

Вільний резерв часу роботи:

- час, на який можна збільшити тривалість роботи, не змінюючи початку наступних подій.

Коефіцієнт напруженості роботи: 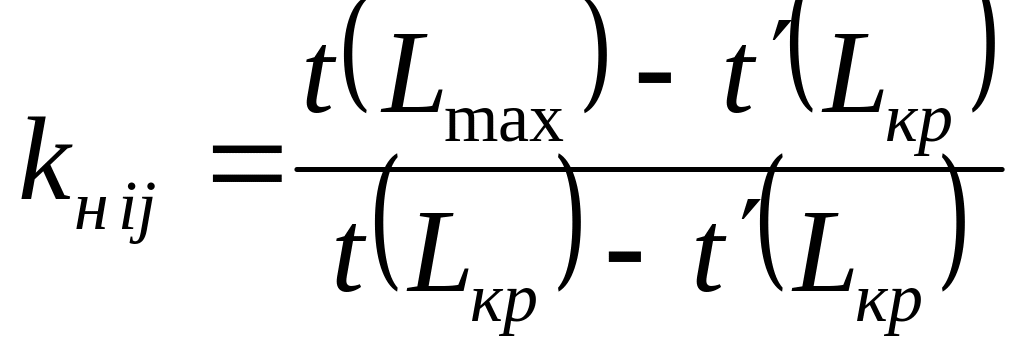, 0…1,

- максимальний повний шлях, що проходить через дану роботу;

- частина даного повного шляху, що співпадає з критичним шляхом;

- тривалість критичного шляху.

Задача:

Для даного сітьового графіка виконати:

1. Пронумерувати події методом «викреслювання дуг»; 2. Визначити: Ранній термін подій; Пізній термін подій; Ранній термін початку робіт; Ранній термін закінчення робіт; Повний резерв часу робіт. 3. Побудувати календарний графік і графік завантаження виконавців. 4. З'ясувати, чи потрібна оптимізація сітьового графіка.

Методичні вказівки.

1. Нумерація подій методом «викреслювання дуг» виконується в такій послідовності: а) знаходитися початкова подія - та, в яку не входить жодна робота, і нумерується - 0. б) викреслюються всі роботи, що витікають з цієї події; в) знаходиться подія, в яку не входить жодна робота (викреслені роботи не вважаються такими, що входять в подію) і нумерується по порядку- 1, 2, 3 і так далі, доки не досягнемо кінцевої події - такої, з якої не виходить жодна робота.

Д ля сітьового графіка, що розглядається нумерація подій виглядає таким чином:

Для даного сітьового графіка експертним шляхом було встановлено максимальну і мінімальну тривалість кожної роботи і число виконавців. Визначаємо очікувану тривалість робіт та дисперсію і результат заносимо в таблицю:

Код робіт (i-j)	0-1	0-2	0-3	1-4	2-4	3-4
Ч - число виконавців	2	1	2	1	1	2
tmin, дн.	2	5	4	1	20	2
tmax, дн.	7	10	9	3	24	7
, дн.	4	7	6	1,8	21,6	4
Dij = (ij)2	1	1	1	0,16	0,64	1

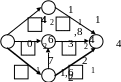
Отриманий результат відображаємо на мережевому графіку: а) над стрілкою проставляємо очікувану тривалість роботи; б) під стрілкою, в квадратику - кількість виконавців. Визначаємо критичний шлях - максимальний повний шлях, що веде від початкової події до кінцевої. Показуємо на графіку.

tкр (0-2-4)= 7+ 21,6= 28,6 дн.

2. Визначаємо:

Ранній термін подій знаходиться послідовно починаючи з початкової події до кінцевої.

	Ранній термін 0 події завжди = 0
	Тільки один шлях з 0 в 1 подію
	Тільки один шлях з 0 в 2 подію
	З двох шляхів, що ведуть з 0 в 3 подію потрібно вибрати максимальний
	Ранній термін кінцевої події завжди = tкр = 28,6

Пізній термін подій - знаходиться послідовно починаючи з кінцевої події до початкової.

	Пізній термін кінцевої події завжди = tкр = 28,6
	Подія 4 (кінцева) і 3 зв'язані тільки одним шляхом 3-4
	Подія 4 (кінцева) і 2 зв'язані двома шляхами: 2-4 і 2-3-4, тоді з tкр потрібно відняти найдовший шлях
	Подія 4 (кінцева) і 1 зв'язані тільки одним шляхом 1-4
	Пізній термін 0 події завжди = 0

Ранній термін початку робіт = ранньому терміну i-ої події	Ранній термін закінчення робіт = ранньому терміну i-ої події+тривалість i-j роботи

Повний резерв часу робіт

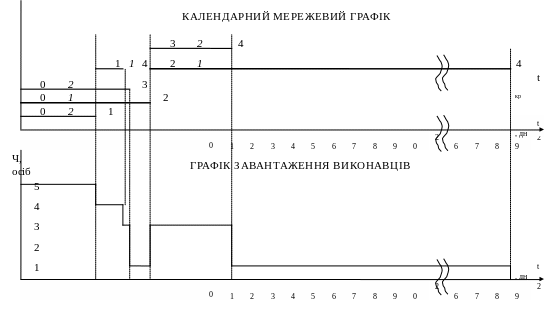
3. Побудуємо календарний графік і графік завантаження виконавців.

Календарний графік будується виходячи з ранніх початків робіт . Календарний графік і графік завантаження виконавців будуються один під одним - масштаб за віссю Х однаковий. Масштаб за віссю Y - довільний. Над роботою проставляється число виконавців. Роботи, що лежать на критичному шляху виділяються штрихуванням (або іншим кольором).

4. З'ясувати, чи потрібна оптимізація сітьового графіка.

Розраховується P(X) вірогідність звершення кінцевої події в заданий (директивний) термін. X - параметр функції розподілу.

,

де - сума дисперсій робіт, що лежать (тільки) на критичному шляху.

Для даного завдання заданий директивний термін t_дир = 25 дн.

.

Потім за таблицею значень функції нормального розподілу знаходимо P(X).

Р(-2,81)  0.

Оскільки отримана вірогідність не потрапляє в діапазон

0,35  P(X)  0,65,

то графік необхідно оптимізувати за критерієм “вірогідність звершення кінцевої події в заданий (директивний) термін”.

Таблиця – Значення функції нормального розподілу

Х	Р(х)	Х	Р(х)	Х	Р(х)	Х	Р(х)
1	2	3	4	5	6	7	8
0,0	0,5	1,6	0,9452	-3,0	0,0013	-1,4	0,0808
0,1	0,5398	1,7	0,9554	-2,9	0,0019	-1,3	0,0968
0,2	0,5793	1,8	0,9641	-2,8	0,0026	-1,2	0,1151
0,3	0,6179	1,9	0,9713	-2,7	0,0035	-1,1	0,1357
0,4	0,6554	2,0	0,9772	-2,6	0,0047	-1,0	0,1587
0,5	0,6915	2,1	0,9821	-2,5	0,0062	-0,9	0,1841
0,6	0,7257	2,2	0,9861	-2,4	0,0082	-0,8	0,2119
0,7	0,758	2,3	0,9893	-2,3	0,0107	-0,7	0,242
0,8	0,7881	2,4	0,9918	-2,2	0,0139	-0,6	0,2743
0,9	0,8159	2,5	0,9938	-2,1	0,0179	-0,5	0,3085
1,0	0,8413	2,6	0,9953	-2,0	0,0228	-0,4	0,3446
1,1	0,8643	2,7	0,9965	-1,9	0,0287	-0,3	0,3821
1,2	0,8849	2,8	0,9974	-1,8	0,0359	-0,2	0,4207
1,3	0,9032	2,9	0,9981	-1,7	0,0446	-0,1	0,4602
1,4	0,9192	3,0	0,9987	-1,6	0,0548	0,0	0,5
1,5	0,9332			-1,5	0,0668

Оптимізується початковий сітьовий графік з обмеженими ресурсами, припускаючи, що всі роботи сітьового графіка дозволяють змінювати їх тривалість пропорційно чисельності виконавців.

При оптимізації перекидаємо виконавців з однієї роботи на іншу (найчастіше на роботи критичного шляху), при цьому змінюється тривалість робіт. Прагнемо, щоб t_кр  t_дир. При цьому прораховуємо Х та Р(Х), доки вірогідність не потрапить в діапазон 0,35  P(X)  0,65. Тоді вважаємо, що оптимізація за цим критерієм виконана.

Наприклад, 1 виконавця з роботи 0-1 (спочатку 4 дні - 2 виконавці) перекинемо на роботу 0-2 (спочатку 7 днів - 1 виконавець). В результаті, робота 0-1 виконуватиметься 8 дн. 1 виконавцем, робота 0-2 виконуватиметься 3,5 дн. 2 виконавцями.

Далі виконується оптимізація за ступінню завантаження виконавців. Оптимізація виконується шляхом переміщення робіт (а також зміни їх тривалості в межах повного резерву) на календарному графіку, таким чином, щоб в кожен момент часу було завантажено однакове число виконавців.

Також можна оптимізувати графік і за іншими критеріями.

Приклад до практичного заняття 4