6. Операции с множествами

Рассмотрим два множества и . Используя их, можно составить новые множества. Например:

• множество , состоящее из всех элементов, принадлежащих хотя бы одному из двух множеств;

• множество , состоящее из всех элементов, принадлежащих обоим множествам;

• множество , состоящее из всех элементов, принадлежащих первому множеству, но не принадлежащих второму, и множество , состоящее из всех элементов, принадлежащих второму, но не первому множеству.

Каждое из этих множеств — это частный случай общей конструкции множества. Рассмотрим эти конструкции по очереди.

Объединение

Определение Пусть и — произвольные множества. Тогда объединение этих множеств — это множество .

Множество из первого пункта списка мы называем объединением наших двух множеств. В более общем случае принимается следующее определение.

О

В повседневной речи пример использования «или» в исключительном смысле — «Чай или кофе?», потому что ответ «И того, и другого!» не предполагается. Пример использования инклюзивного «или» — «Молока или сахара?», потому что тут можно ответить «И того, и другого».

братите внимание, что слово «или» в этом определении используется в инклюзивном смысле «и/или», то есть состоит из элементов и элементов , включая элементы, входящие и в , и в .

Пример 1.6

Решение

Упражнение 1.15

Пока что мы дали определение объединения двух множеств. Так же можно дать и определение объединения большего числа множеств; например, объединение множеств , и — это множество .

Пересечение

Множество из второго пункта списка мы называем объединением наших двух множеств. В более общем случае принимается следующее определение.

Определение Пусть и — произвольные множества. Тогда их пересечением называется множество .

Два множества, у которых нет общих элементов, например, и , называются непересекающимися. Тогда говорят, что ⌀.

Пример 1.7

Решение

Упражнение 1.16

Пока что мы дали определение пересечения двух множеств. Так же можно дать и определение пересечения большего числа множеств; например, пересечение множеств , и — это множество .

Разность

П

Определение Пусть и — произвольные множества. Тогда разностью и называется множество .

ервое множество из третьего пункта списка мы называем вычитанием второго множества из первого, а второе — вычитанием первого множества из второго. В более общем случае принимается следующее определение.

З

В некоторых текстах разность обозначается как .

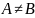амечание Обратите внимание, что если , то . Также для любого ⌀.

Пример 1.8

Решение

Упражнение 1.17