
- •Множества
- •Что такое множество?
- •Система записи множеств
- •М Такие множества появляются во многих приложения математики, например, в компьютерной графике. Ножества на плоскости
- •Окружности
- •Полуплоскости, круги и другие множества на плокости
- •Равенство множеств и подмножества
- •Вычисление подмножеств конечных множеств
- •Операции с множествами
- •Объединение
- •Пересечение
- •Разность
Равенство множеств и подмножества
Рассмотрим множества
 и
и
 .
Хотя эти множества написаны в разных
формах, каждое из них содержит в точности
одни и те же элементы, 1 и –1. Мы называем
такие множества равными.
.
Хотя эти множества написаны в разных
формах, каждое из них содержит в точности
одни и те же элементы, 1 и –1. Мы называем
такие множества равными.
Определение Множества A и B называются равными, если они содержат в точности одни и те же элементы. Пишут A = B.
Когда два множества содержат малое количество элементов, обычно можно проверить, являются ли они одними и теми же, и из этого определить равенство множеств.
Упражнение 1.8
Если же множества содержат много элементов, уже не так просто определить, равны ли они. Опишем метод работы с такими случаями, предварительно введя одну необходимую идею.
Рассмотрим множества
 и
и
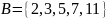 .
Каждый из элементов
.
Каждый из элементов
 является и элементом
является и элементом
 .
Говорят, что
— это подмножество
.
.
Говорят, что
— это подмножество
.
И
Определение Множество
— подмножество
множества
,
если каждый элемент
— это также элемент
.
Также говорят, что
содержится
в
:
 .
.
Не
путайте символы
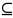 и
и
 .
Например, мы пишем, что
.
Например, мы пишем, что
 ,
поскольку
,
поскольку
 — это подмножество
— это подмножество
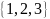 ,
и
,
и
 ,
поскольку 1 — это элемент
.
,
поскольку 1 — это элемент
.
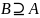 ,
то есть «
содержит
».
Чтобы показать, что
— не подмножество
,
пишут
,
то есть «
содержит
».
Чтобы показать, что
— не подмножество
,
пишут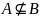 или
или
 ,
то есть «
не содержит
».
,
то есть «
не содержит
».
Когда нужно определить, является ли данное множество A подмножеством данного множества , подход зависит от способа, которым определены множества. Если содержит малое число элементов, то мы просто проверяем каждый элемент на принадлежность . Иначе надо проверить, отвечает ли произвольный элемент требованиям принадлежности , как показано ниже в примере 1.2.
Чтобы показать, что данное множество — не подмножество данного множества , нужно найти хотя бы один элемент , который не принадлежит . Пустое множество ⌀ является подмножеством любого множества, поскольку невозможно найти элемент ⌀, который бы не принадлежал данному множеству.
Пример 1.2
Решение
Упражнение 1.9
Если два множества
и
равны, то
— это подмножество
и наоборот. Если
— подмножество
,
но не равно ему, то говорят, что
— собственное подмножество
,
и пишут
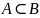 или
или
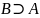 .
.
Чтобы показать, что — это собственное подмножество , нам нужно показать, что — это подмножество и что есть хотя бы один элемент , не содержащийся в .
Пример 1.3
Решение
Упражнение 1.10
Теперь вернёмся к вопросу, как определить, равны ли множества и , если в обоих много элементов. Для этого надо показать, что каждое из множеств — подмножество другого.
П
Стратегия 1.1 Чтобы показать, что множества и равны:
покажите, что ;
покажите,
что
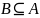 .
.
Решение
Упражнение 1.11
Вычисление подмножеств конечных множеств
К
Ноль элементов — в пустом множестве.
онечное множество — это множество с конечным количеством элементов, то есть число элементов — это некоторое натуральное число или 0. Ранее мы увидели, что, используя систему записи множеств, мы можем писать элементы множества в любом порядке. Например, множество {1, 2, 3} может быть при переставлении элементов местами записано шестью разными способами: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1} (каждый из элементов написан по разу).В
Определение Для
любого положительного целого числа

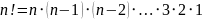 ,
,
Также
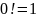 .
.
 способами, поскольку первый элемент
можно выбрать
способами, второй —
способами, поскольку первый элемент
можно выбрать
способами, второй —
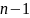 и т. д. Это произведение мы обозначаем
как
и т. д. Это произведение мы обозначаем
как
 (читается как
факториал).
(читается как
факториал).
Н
 определяется
равным 1 для удобства, чтобы для
определяется
равным 1 для удобства, чтобы для
 было верным соотношение
было верным соотношение
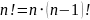 Также это определение показывает, что
число различных упорядоченных вариантов
пустого множества — 1: нельзя менять
порядок нуля элементов!
Также это определение показывает, что
число различных упорядоченных вариантов
пустого множества — 1: нельзя менять
порядок нуля элементов!
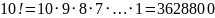
способами.
Конечное множество
имеет конечное число подмножеств, но
сколько их? Например, рассмотрим множество
{1, 2, 3}. Ниже перечислены все подмножества
этого множества в соответствии с их
размером
 :
:
-
подмножества
число подмножеств
0
⌀
1
1
{1}, {2}, {3}
3
2
{1,2}, {1,3}, {2,3}
3
3
{1, 2, 3}
1
Таблица показывает,
что множество имеет в общей сложности
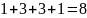 подмножеств.
подмножеств.
Упражнение 1.12
Видим, что множество
из трёх элементов имеет 8 подмножеств,
а множество из четырёх элементов — 16
подмножеств. Можно предположить, что
множество из
элементов имеет
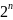 подмножеств. Чтобы это доказать,
предположим следующее. С каждым
подмножеством множества
,
состоящего из
элементов, можно сопоставить строку из
символов, где
подмножеств. Чтобы это доказать,
предположим следующее. С каждым
подмножеством множества
,
состоящего из
элементов, можно сопоставить строку из
символов, где
 -й
символ — это 1, если
-й
элемент
содержится в данном подмножестве, и 0
иначе. Например, если
-й
символ — это 1, если
-й
элемент
содержится в данном подмножестве, и 0
иначе. Например, если
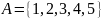 ,
то строка для подмножества
,
то строка для подмножества
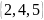 —
это 01011. Поскольку для каждого из
символов есть два варианта выбора, то
всего строк, как и подмножеств,
.
—
это 01011. Поскольку для каждого из
символов есть два варианта выбора, то
всего строк, как и подмножеств,
.
Теперь сосредоточимся
на таком вопросе, который связан с
предыдущим: сколько у множества из
элементов подмножеств из
элементов? Чтобы ответить на него,
рассмотрим упорядоченный выбор
элементов из множества. Для первого —
вариантов, для второго
,
для последнего —
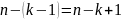 .
Таким образом, количество упорядоченных
наборов из
элементов
-элементного
множества равно
.
Таким образом, количество упорядоченных
наборов из
элементов
-элементного
множества равно
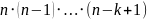 .
Но некоторые из этих наборов порождают
одни и те же множества. На самом деле
каждое подмножество из
элементов соответствует
.
Но некоторые из этих наборов порождают
одни и те же множества. На самом деле
каждое подмножество из
элементов соответствует
 выборам
элементов. Таким образом, число различных
подмножеств c
элементами
-элементного
множества равно
выборам
элементов. Таким образом, число различных
подмножеств c
элементами
-элементного
множества равно
 .
.
У
Определение Для
любых неотрицательных целых
и
,
 ,
,
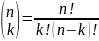 .
.
Это выражение называется биномиальным коэффициентом. Это число -элементных подмножеств -элементного множества.
множив числитель и знаменатель на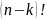 ,
получим
,
получим
 .
Введём для этого выражения такую запись.
.
Введём для этого выражения такую запись.
Н
Выражение
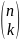 иногда записывается как
иногда записывается как
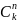 ,
что читается как «цэ из эн по ка».
,
что читается как «цэ из эн по ка».
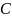 означает combination
— комбинация. Причина наименования
«биномиальный коэффициент» станет
ясна в четвёртой главе.
означает combination
— комбинация. Причина наименования
«биномиальный коэффициент» станет
ясна в четвёртой главе.
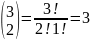 ,
,
что мы и получили из таблицы на странице 14.
Более интересный пример — пример лотереи, в которой участники выбирают подмножество из 6 элементов множества из 49 элементов. В этом случае возможных подмножеств, или, как их обычно называют, комбинаций,
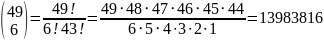
Конечно,
в знаменателе можно отбросить
 и писать
и писать
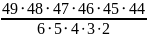 .
.
Упражнение 1.13
Пример 1.5
Решение
Упражнение 1.14
