5. Приклад виконання завдання

1. Вказівка шифру завдання. Варіант Я35

2. Представлення розрахункової схеми і початкових даних.

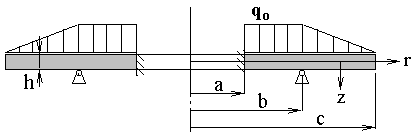
Рис. 5.1. Розрахункова схема

На схемі показана система координат. Для осі z (відповідно для прогину w і нормального тиску q ) позитивним вважається напрям вниз.

Таблиця 2. Початкові дані

a	b	с	h	qo	E	v
м	м	м	мм	МПа	Мпа
0.10	0.30	0.40	5	0.4	2·105	0.3

Розрахункова схема містить 2 чинники, кожний з яких вимагає розбиття пластини на ділянки:

наявність проміжної опори на колі ;

зміна характеру зовнішнього навантаження уздовж лінії .

Тому необхідно розглянути дві ділянки радіуса пластини:

при цьому точки кола одночасно належать обом ділянкам.

У запропонованому прикладі приведене рішення варіанта Я35.

Рішення рівняння Софі Жермен

3. Формулювання задачі. Диференціальні рівняння відносно прогину пластини :

I ділянка (5.1)

II ділянка (5.2)

Граничні умови:

жорстке защемлення: (5.3)

вільний край: (5.4)

Рівність (5.4) відносно прогину виходить з (2.5) і (2.6):

(5.5)

Умови сполучення на границі ділянок

(5.6)

Остання рівність з урахуванням постійності жорсткості :

(5.7)

4. Відшукання загального рішення. Послідовне інтегрування рівняння (5.1) приводить до наступних виразів :

(5.8)

(5.9)

(5.10)

(5.11)

у яких С₁, С₂, С₃, С₄ - невизначені константи.

Аналогічно з (5.2) виходить:

(5.12)

(5.13)

(5.14)

(5.15)

5. Отримання системи рівнянь для пошуку констант. Константи інтегрування С₁ - С₈ визначаються із співвідношень (5.3), (5.5), (5.6) і (5.7):

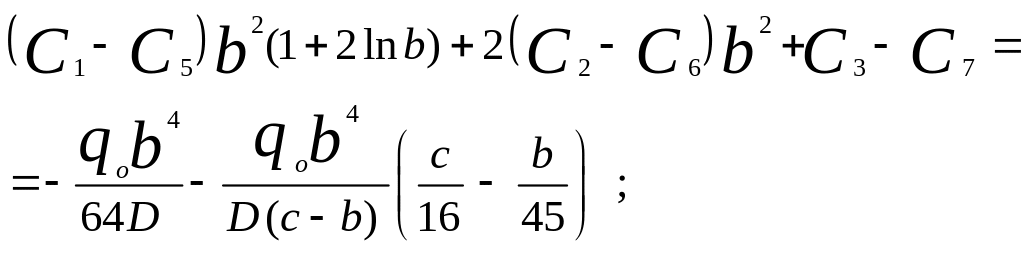
(5.16)

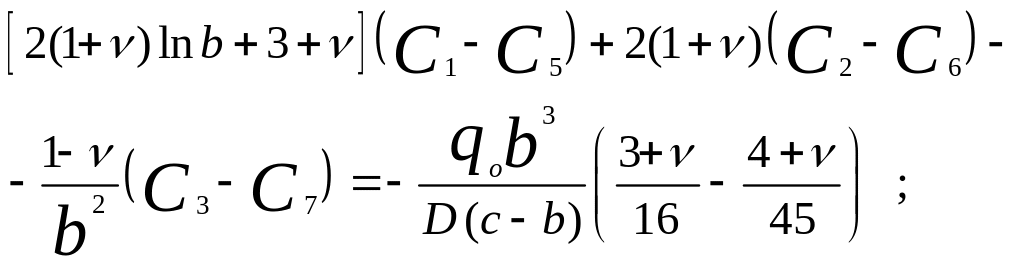
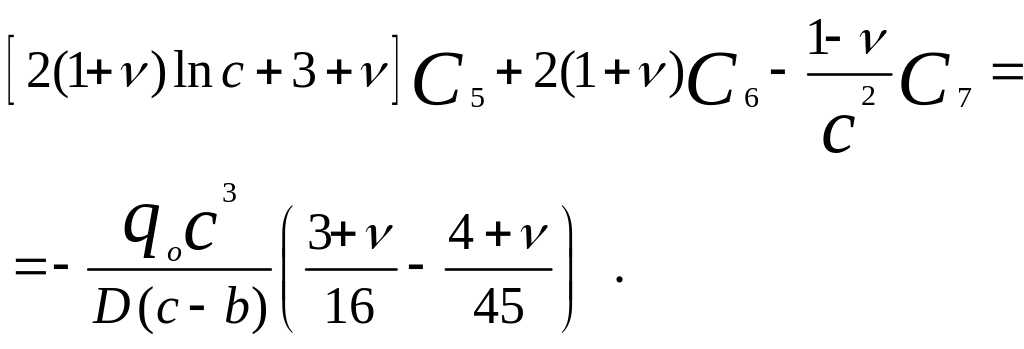
Система лінійних відносно С₁ - С₈ рівнянь (5.16) може бути представлена в канонічній формі:

(5.17)

де {Х}={С₁ С₂ С₃ С₄ С₅ С₆ С₇ C₈ }^Т - вектор невідомих; [А] - матриця коефіцієнтів розміру 8x8; { В} - вектор правих частин.

Для вирішення СЛАР вигляду (5.17) методом виключення Гауса можна застосувати стандартну програму gauss.exe . При її виклику необхідно задати розмірність системи N, елементи матриці [А] і вектора {В}. Для системи (5.16) N = 8 ; значення компонент [А] і {В}приведені в табл.3. Можливо також скористатися програмним пакетом комп’ютерної алгебри Maple.

Таблиця 3. Коефіцієнти рівняння

aij									bi
i\j	1	2	3	4	5	6	7	8
1	-2.303 *10-2	0.01	-2.303 *10-2	1	0	0	0	0	-2.730 *10-4
2	-3.605 *10-2	0.02	1	0	0	0	0	0	-1.092 *10-3
3	-1.084 *10-1	0.09	-1.204	1	0	0	0	0	-2.211 *10-2
4	0	0	0	0	-1.084 *10-1	0.09	-1.204	1	-6.958 *10-2
5	-1.267 *10-1	0.18	1	0	1.267 *10-1	-0.18	-1	0	1.710 *10-1
6	3.884 *10-4	5.952 *lO3	-1.781 *10-2	0	-3.884 *10-4	-5.952 *10-3	1.781 *10-2	0	1.196 *10-2
7	0	0	0	0	1	0	0	0	-4.659
8	0	0	0	0	9.176 *10-1	2.60	-4.375	0	-1.238 *101

6. Рішення СЛАР. В результаті рішення одержано: С₁ = -9.40211·10-1; С₂ = -1.0966 ; С₃ = -1.3057·10-2; С₄ = -4.1021·10-2; С₅ = -4.6592 ; С₆ = -3.4931 ;С₇ = -2.2393·10-1 ; C₈= -5.2967·10-1.

7. Запис виразів для шуканих величин. Підстановка знайдених констант в (5.11) і (5.15) з використанням формули (2.5) приводить до остаточних виразів прогину, перерізуючої сили і згинаючих моментів для двох ділянок пластини:

I ділянка a  r  b:

(5.18)

II ділянка b  r  c:

(5.19)

8. Графічне зображення результатів. Розподілення уздовж радіусу пластини прогину, перерізуючої сили, радіального і окружного згинаючих моментів показані відповідно на рис. 5.4 - 5.7

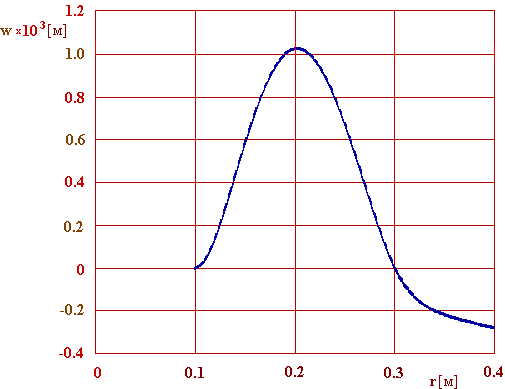
Рис. 5.4. Прогин пластини

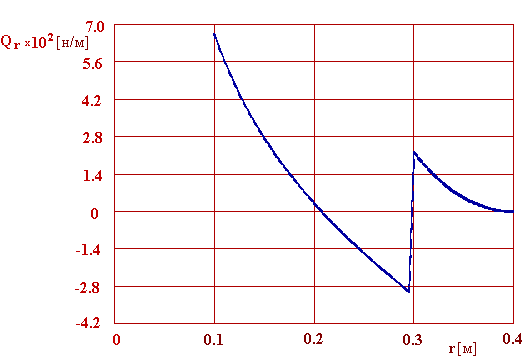
Рис. 5.5. Перерізуюча сила

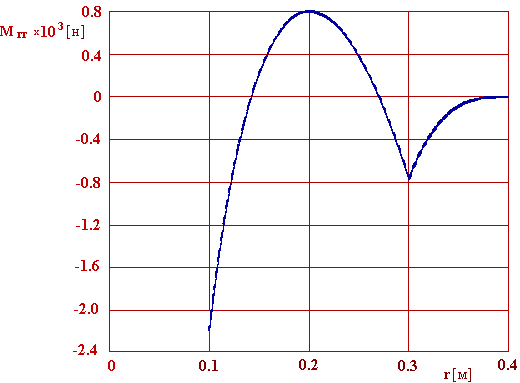
Рис. 5.6. Радіальний згинаючий момент

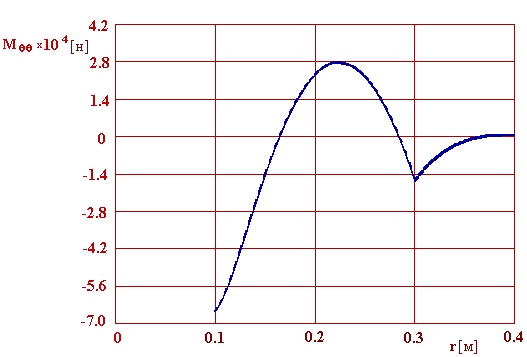
Рис. 5.7. Окружний згинаючий момент

9. Підрахунок напружень. Найбільші нормальні напруження:

- радіальне

- окружне

Найбільше дотичне напруження