МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

«Харківський політехнічний інститут»

Г. І. Львов, В. Г. Сукіасов

АНАЛІЗ ОСЕСИМЕТРИЧНОГО ЗГИНУ

КРУГЛИХ І КІЛЬЦЕВИХ ПЛАСТИН

Методичні вказівки

Харків

2011

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

«Харківський політехнічний інститут»

Г. І. Львов, В. Г. Сукіасов

АНАЛІЗ ОСЕСИМЕТРИЧНОГО ЗГИНУ

КРУГЛИХ І КІЛЬЦЕВИХ ПЛАСТИН

Методичні вказівки

до індивідуальних домашніх завдань з курсу

«Теорія пластин і оболонок»

для студентів спеціальності 8.04020203 «Комп’ютерна механіка»

Затверджено редакційно-видавничою радою університету, протокол № від р.

Харків

НТУ «ХПІ»

2011

Аналіз осесиметричного згину круглих і кільцевих пластин. Методичні вказівки до індивідуальних домашніх завдань з курсу «Теорія пластин і оболонок» для студентів спеціальності 8.04020203 «Комп’ютерна механіка» / уклад. Г. І. Львов, В. Г. Сукіасов. – Х. : НТУ «ХПІ», 2011. – с.

Укладачі:   Г. І. Львов

  В. Г. Сукіасов

Рецензент   О. К. Морачковський

Кафедра динаміки та міцності машин

1. Загальні положення

Індивідуальні домашні завдання по курсу теорії пластин і оболонок виконуються з метою закріплення теоретичних знань і придбання практичних навиків розрахунку конструкцій. Виконання завдання припускає використання персонального комп'ютера, зокрема, для вирішення системи лінійних алгебраїчних рівнянь.

Перед виконанням роботи слід ретельно вивчити відповідні розділи теорії [1,2].

Робота виконується в окремому зошиті і здається на перевірку викладачу не пізніше за два тижні з моменту отримання завдання. Оцінка роботи здійснюється по наступних основних параметрах:

• повнота і правильність виконання завдання;

• акуратність оформлення;

• своєчасність здачі.

2. Зміст завдання

Об'єктом дослідження є осесиметрична конструкція у вигляді круглої або кільцевої пластини кусково постійної товщини.

Метою розрахунку є визначення компонент напружено-деформованого стану (н.д.с.) пластини під дією заданого поперечного навантаження у вигляді нормального тиску q, зусилля Q, що розподілене по колу, або сили Р в центрі круглої пластини. Можлива також дія рівномірно розподіленого по контуру згинаючого моменту М_о. Дана пластина задовольняє наступним вимогам:

пластина є тонкою з відношенням товщини до радіусу не більше 1/20, тому для неї справедливі гіпотези Кирхгофа;

пластина виготовлена з ізотропного матеріалу, що підкоряється закону Гука;

пластина жорстка, тобто її максимальний прогин не перевищує 1/4 товщини.

Кожен студент одержує індивідуальний шифр завдання, що містить букви і числа. Буквений індекс відповідає розрахунковій схемі, а число указує рядок в таблиці початкових даних розд.4. Початкові дані включають геометричні розміри а, b, с, Н, h і параметри зовнішнього навантаження q, Q. Р, М₀. Слід використовувати тільки величини, представлені на розрахунковій схемі. Пружні характеристики матеріалу однакові для всіх варіантів і складають: Е =2·10⁵ МПа, v = 0.3.

Розрахунок пластини в рамках вказаних вище обмежень зводиться до відшукання прогину w її серединної площини шляхом рішення лінійної крайової задачі для рівняння Софі Жермен

(2.1)

яке для осесиметричної круглої пластини має вигляд

(2.2)

де ~ жорсткість згину пластини.

Після розкриття дужок в (2.2) виходить диференціальне рівняння 4-го порядку із змінними коефіцієнтами

(2.3)

Його загальне рішення включає рішення однорідного рівняння, що одержується за допомогою підстановки Ейлера , і часткове рішення, залежне від виду функції q(r).

Рішення рівняння (2.2) можна також одержати, якщо врахувати, що

Це дозволяє привести (2.2) до вигляду, зручному для безпосереднього інтегрування:

(2.4)

Загальне рішення рівняння (2.2) у формі (2.3) або (2.4) містить 4 константи інтегрування, що визначаються з граничних умов.

Кінцевим результатом розрахунку є залежності від радіальної координати r прогину пластини w, радіального перерезізуючого зусилля Q_r згідно з (2.5):

(2.5)

а також радіального М_rr і окружного М_θθ згинаючих моментів. Останні визначаються по формулах

(2.6)

Крім цього, необхідно знайти положення точок, в яких мають місце найбільші напруження, і значення цих напружень. Згідно гіпотезам Кирхгофа нормальні напруження лінійно розподілені по товщині пластини:

, (2.7)

а дотичні - по квадратичному закону:

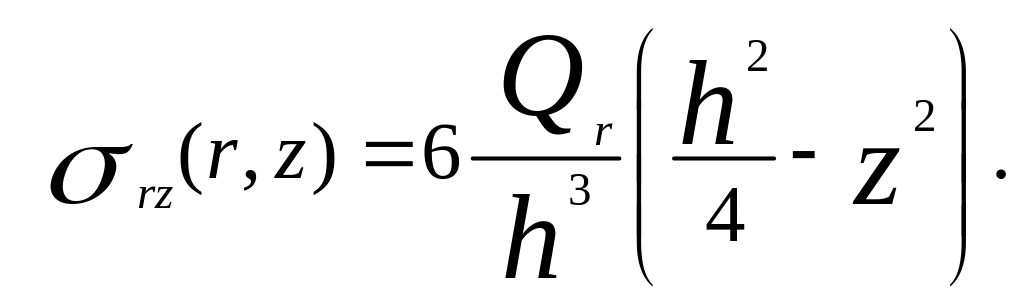(2.8)

Тому шукані величини можуть бути знайдені по формулах

(2.9)

у котрих - точки максимуму абсолютних значень відповідно M_rr, M_θθ і Q_r.

При дії на пластину зосередженої сили Р має місце необмежене зростання M_rr, M_θθ і Q_r і відповідних напружень поблизу точки r = 0. Необхідно пам'ятати, що такий результат виходить на основі допущень елементарної теорії тонких пластин, що втрачають силу при ; зокрема нехтування напруженнями в цьому випадку необґрунтоване. Коректне визначення компонент н.д.с. в околі точки прикладення сили Р можливо з позицій 3-мірної теорії пружності, тоді як результати елементарної теорії можна вважати достовірними тільки для точок, віддалених від центру на відстань в декілька товщин пластини [1]. Тому для задач вказаного типа рекомендується починати побудову графіків згинаючих моментів і перерізуючої сили, а також підрахунок напружень з точки .