2.2. Расчет элементов верхнего пояса балки

Сечение 5, нормальное к продольной оси элемента, N=1057,64 кН, M=44,22кН·м, N_l=658,35 кН, M_l=27,53 кН·м.

Находим м=41,8 мм, поскольку случайный эксцентриситете мм 41,8 мм, то оставляем для расчета 41,8 мм.

Определим мм.

Требуемая площадь сечения продольной рабочей арматуры класса A-III (R_s=R_sc=365 МПа). Предварительно вычислим коэффициенты и :

;

Тогда по формулам (123) и (124) [6] получим:

106,01 мм² < 0

мм² < 0.

Принимаем в сжатой и растянутой зонах конструктивное армирование по 2Ø10 А-III, мм² > мм².

Элемент 1 – 2, сечение, наклонное к продольной оси, Q=44 кН, N=922,14кН. Так как при расчете прочности по наклонным сечениям нижнего пояса балки несущая способность оказалась меньше требуемой, то с учетом перераспределения усилий будем проектировать поперечную арматуру в верхнем поясе на восприятие поперечной силы кН. Расчет выполняем согласно пп. 3.21-3.30 [6].

Проверим условие (92) [6] кН > кН, т. е. условие выполняется.

Проверим условие (93) [6], принимая значение с равным , но не более пролета 700 мм. Для этого определим значения и , принимая > 0,5, принимаем =0,5 и =1 п. 3.32 [2].

Тогда кН. Статический момент части сечения, расположенной выше оси, проходящей через центр тяжести, мм³. Из графика 18 [6] при , находим τ=2,6, т.е: τ_xy,crc=τ∙R_bt=2,2·1,3=2,86 МПа.

Тогда: кН

где: мм⁴.

Вычисляем: мм и менее пролета 700 мм.

Поскольку : кН то прочность наклонного сечения обеспечена без поперечной арматуры. С учётом конструктивных требований для сжатых элементов принимаем поперечную арматуру для верхнего пояса балки диаметром 4 мм класса Вр–I, с шагом 20∙d=20·10=200 мм.

2.3. Расчет стоек балки

Стойки решетчатой балки рассчитываются на неблагоприятные сочетания усилий N и М без учета длительности действия нагрузок, так как всегда . Рассмотрим порядок определения площади сечения продольной рабочей арматуры в сжато-изогнутой стойке 17-18, N=2,32 кН, М=19,6 кН·м, – М= –9,32кН·м.

_{Сначала определим сечение продольной рабочей арматуры у наиболее растян}утой грани (слева) при действии изгибающего момента М=+М=19,6 кН·м. Вычисляем эксцентриситеты и :

м=8448 мм;

мм.

Расчет сечения несимметричной продольной арматуры выполняем по формулам (121) – (129) [4]. Поскольку:

мм² < 0, то расчет ведем без учета сжатой арматуры.

Находим , соответственно по приложению IV [8] находим 0,0203, тогда мм².

Принимаем у левой грани 2Ø10 А-III, мм² > мм².

Требуемая площадь сечения растянутой арматуры у правой грани при действии М=|–M|=9,32 кН·м. по аналогичному расчету составит =66,9 мм². По приложению IV [8] принимаем и у правой грани 2Ø10 А-III.

2.4. Расчет прочности по наклонному сечению опорной части балки

Подбор поперечной арматуры в опорной части балки выполняем согласно пп. 3.22, 3.23 и 3.26 [4] на действие поперечной силы кН с учетом усилия обжатия Р=477,3 кН. Рабочая высота в конце наклонного сечения будет равна:

мм.

Определим значение и для чего находим:

< 0,5.

Тогда кН;

кН.

Определим требуемую интенсивность хомутов, принимая длину проекции наклонного сечения равной расстоянию от опоры до первого груза с₁=2850 мм, где поперечная сила кН.

Находим кН> кН.

Тогда .

Поскольку с₁=2850 мм > h₀=2∙1000,5=2001 мм, то принимаем с₀=2001 мм, в этом случае будем иметь: .

Так как =0,133 < =0,651, то требуемая интенсивность хомутов находим: Н/мм.

Согласно п. 5.42 [4], шаг хомутов должен быть не более 1/3h₁=890/3=297 мм и не более 500 мм. Максимально допустимый шаг хомутов по формуле (67) [6] равен:

мм.

Назначаем шаг хомутов s=250 мм, тогда получим мм². Принимаем двухветвевые хомуты диаметром 8 мм из стали класса А-I (А_sw.fact=101 мм²).

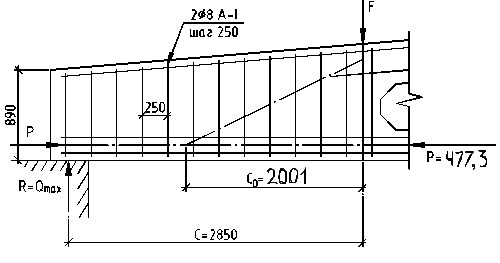
Рис. 6. К расчету прочности опорной части балки по наклонному сечению