3.3. Вычисление величин посредством криволинейного интеграла
1) Длина дуги АВ плоской или пространственной линии
2) Площадь фигуры, расположенной в плоскости хОу и ограниченной замкнутой линией С
3) Масса материальной дуги АВ
где линейная плотность вещества в точке М дуги.
4) Координаты центра тяжести С дуги АВ
5)
Работа,
совершаемая силой
действующей
на точку при перемещении её по дуге
АВ
Пример 30. Найти площадь, ограниченную замкнутой кривой - эллипсом
х = a cost, у = bsint.
Пример
31.
Найти массу дуги АВ
кривой
если
в каждой её точке линейная плотность
пропорциональна квадрату абцисы точки;
хA
=
1;хB
=3.
Решение.
Пример
32.
Найти работу силового поля
вдоль
окружности
по часовой стрелки.
3.4. Формула Грина для плоскости
Если
L
- граница области D
и функции
непрерывны,
вместе со своими частными производными
1-го порядка, в замкнутой области D,
то справедлива формула Грина
обход
контура выбирается положительным
Пример 33. Вычислить криволинейный интеграл непосредственно и с помощью формулы Грина
где L - периметр треугольника с вершинами А(-1;0), В(0,2) и С(2;0).
Решение.
Сделаем рисунок 39. Составим уравнение
АВ:
Составим уравнение ВС:
Составим уравнение СА:
Рис.
39
Следовательно,
Вычислим криволинейный интеграл с помощью формулы Грина
33.5. Восстановление функции по ее полному дифференциалу
Если
известен полный дифференциал функции
двух переменных
где
то
ее можно найти интегрируя
по любой линии между произвольной
фиксированной точкой
и переменной точкой
(3.1)
Обычно
в качестве линии интегрирования АМ
берется ломаная AN1M
или
AN2M
со
звеньями, параллельными осям координат
(рис. 40). При этом криволинейный интеграл
наиболее
просто выражается через обыкновенные
интегралы, и формула (3.1) преобразуя к
виду
Во
многих случаях можно найти функцию
по ее полному дифференциалу
иначе.
Поскольку
полный дифференциал равен сумме частных
дифференциалов
то интегрируя каждый из них отдельно,
найдем два выражения искомой функции
:
а)
считая
у
постоянной;
б)
считая
х
постоянной;
где
и
-
неизвестные функции.
Беря все известные члены из первого выражения и дописав к ним недостающие члены, зависящие только от у, из второго выражения получим функцию u.
y
должен быть тождествен данному полному
дифференциалу
N2(x0,y)
M(x,y)
A(x0,y0)
N1(x,y0)
x
0
Рис. 40
Пример
34. Проверить,
что данное выражение является полным
дифференциалом функции
,
и найти u:
1)
2)
3)
Решение.
1)
Обозначим коэффициенты при дифференциалах
и
найдем
и
Так как здесь
и
непрерывны, то заданное выражение
является полным дифференциалом некоторой
функции u.
Найдем эту функцию по формуле (3.2), выбрав точку А в начале координат О(0,0)
2)
Преобразуем заданное дифференциальное
выражение к виду
и найдем
:
Условие
выполнено. Заданное выражение есть
полный дифференциал некоторой функции
Найдем эту функцию по формуле (3.3):
где
3) В начале находим частные производные
и
убеждаемся, что они тождественно равны
и что заданное выражение есть полный
дифференциал некоторой функции
Затем
найдем эту функцию вторым способом,
интегрируя каждый частный дифференциал
и
отдельно.
а)
считая
у
постоянной;
б)
считая
х
постоянной.
Объединяя эти два выражения – дописав к известным членам первого выражения недостающий член, зависящий только от у, из второго выражения получим одну из первообразных функций, а прибавив к ней произвольную постоянную С, получим общее выражение первообразной функции для заданного полного дифференциала
П
ример
35.
Дано: dU = 2xydx + x2dy.
Найти U(x,y).
Решение.
Выбираем начальную точку М0 - пусть М0(1,0), а путь интегрирования М0M - по звеньям ломаной М0AM, тогда
Задача 1. Изменить порядок интегрирования.
Задача 2. Вычислить двойные интегралы:
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а) ;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а) ; .
б)
;
.
а) ; .
б)
;
.
а)
;
.
б)
;
.
а) ; .
б)
;
.
Задача 3. Вычислить тройные интегралы:
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а) ;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
а)
;
.
б)
;
.
Задача 4. Найти площадь фигуры, ограниченной данными линиями.
.
.
.
.
.
.
.
.
.
.
Задача 5. Пластинка D задана ограничивающими ее плоскостями, µ- поверхностная плотность. Найти массу пластинки.
.
.
.
.
.
.
.
.
.
.
Задача 6. Найти объем тела, заданного ограничивающими его поверхностями.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Задача 7. Тело V задано ограничивающими его поверхностями, m - плотность. Найти массу тела.
.
.
.
.
.
Задача 8. Вычислить интегралы
по дуге синусоиды
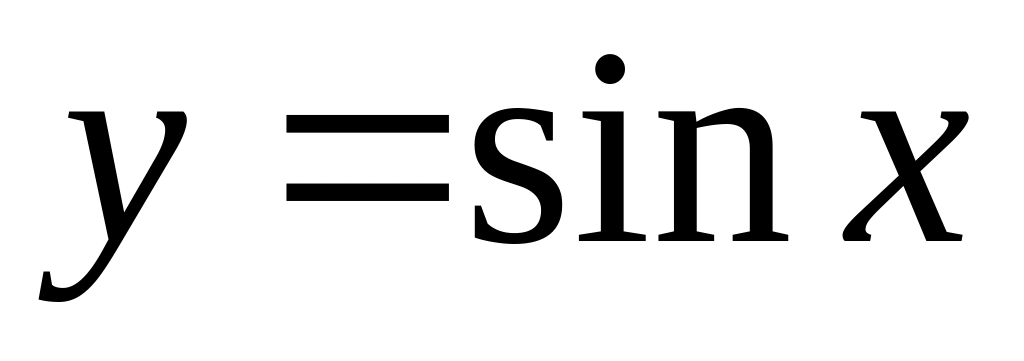от
до
.
по кривой
от точки
до точки
.
по кривой
от точки
до точки
.
по параболе
от точки
до точки
.
по параболе
от точки
до точки
.
по кривой
от точки
до точки
.
по кривой
от точки
до точки
.
по кривой
,
,
.
,
где
- контур треугольника
с вершинами
,
,
.
,
где
- прямая, соединяющая точки
и
.
,
где
- отрезок прямой от
до
.по отрезку прямой от точки до точки
.
по отрезку прямой
от точки
до точки
.
по кривой
,
,
.
,
если
,
,
.
,
где
- отрезок прямой от
до
., где - парабола
,
соединяющая точки
и
., где - ломаная, проходящая через точки ,
и
.
,
если
- ломаная
,
где
,
,
,
если
- дуга полукубической параболы
от
до
.
Задача
9. Проверить,
что данное дифференциальное выражение
есть полный дифференциал некоторой
функции
и
затем найти u:
