2.6. Приложение тройного интеграла в механике

1. Определение массы тела, занимающего область V

где объёмная плотность распределения массы в точке тела.

2. Координаты центра тяжести С тела

где - статистические моменты тела относительно координатных плоскостей

Для однородного тела выносится за знак интегралов и сокраща­ется.

3. Моменты инерции тела относительно осей ОХ, OУ и OZ и начала коор­динат 0.

Пример 26. Найти массу тела, ограниченного цилиндрической поверхно­стью и плоскостями если в каждой его точке объём­ная плотность численно равна ординате этой точки.

Решение. Согласно условию в точке тела объёмная плотность

где V - область, занимаемая данным телом (рис. 36).

Рис. 36 Рис.37

Пример 27. Найти момент инерции однородного полого усечённого ци­линдра (рис. 37) относительно его оси.

Решение. Обозначим внешний и внутренний радиусы цилиндра через R и r, а его высоту через Н. Тогда относительно указанной на рис. прямоугольной системы координат уравнения цилиндрических поверхностей и плоскостей, ог­раничивающих цилиндр (V), будут

Полагая , получим момент инерции цилиндра относительно его оси в ходе решения перейдём в полярную систему координат.

Криволинейные интегралы

3.1. Определение криволинейного интеграла первого рода

Пусть - непрерывная функция и ) - уравнение некоторой гладкой кривой S.

Построим систему точек (i=0,l,2,...,n), разбивающих кривую S на элементарные дуги , и составим интегральную сумму при и называется криволинейным интегралом первого типа

(dS - дифференциал дуги) и вычисляется по формуле

В случае параметрического задания кривой S: име­ем:

Рассматриваются также криволинейные интегралы первого типа от функ­ции трёх переменных , взятые по пространственной кривой, которые вы­числяются аналогично. Криволинейный интеграл 1-го типа не зависит от на­правления пути интегрирования.

П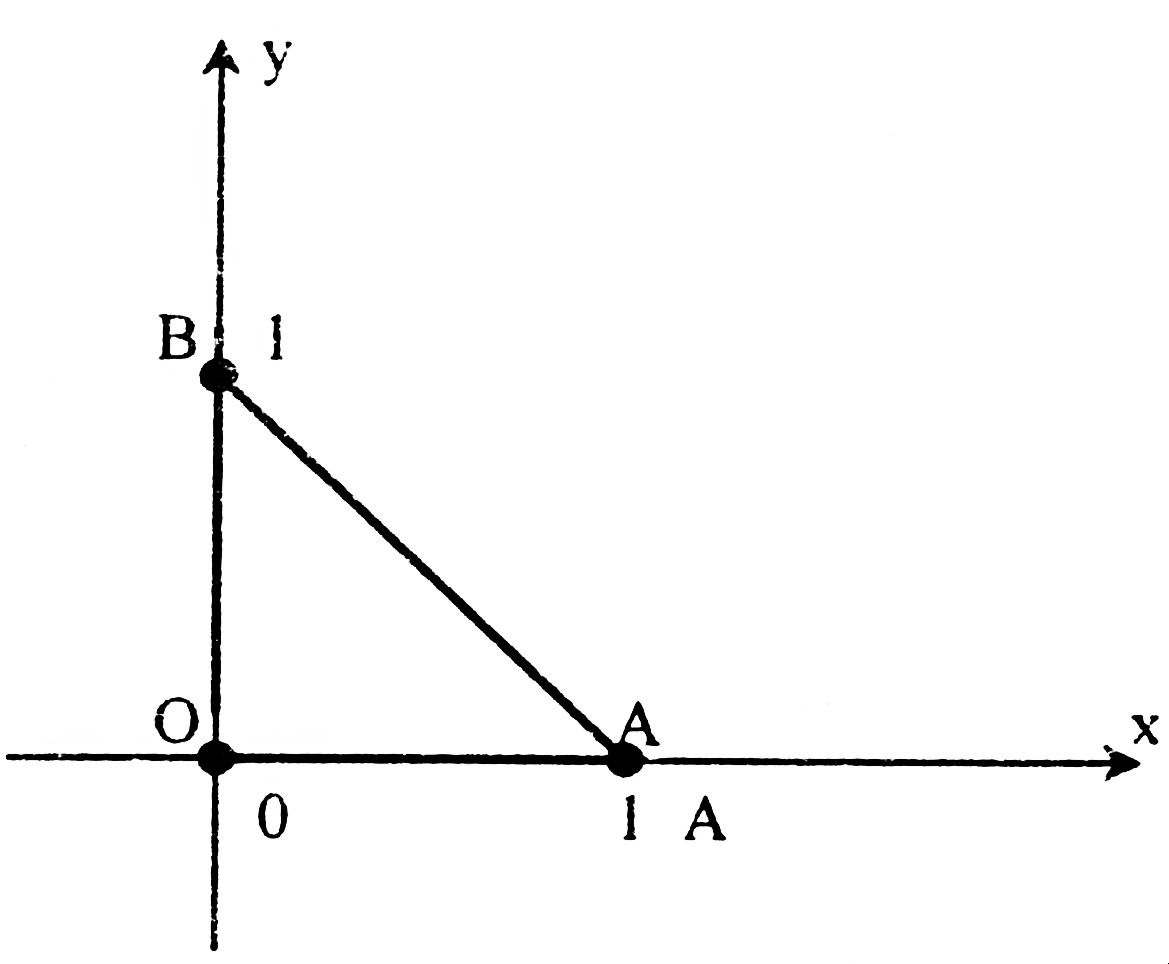 ример 28. Вычислить кри­волинейный интеграл ,

где С - контур треугольника АВО с вершинами А(1;0), В(0;1) и О(0;0) (рис. 38).

Решение. Уравнение АВ: уравнение АВ: уравне­ние OA:

Рис. 38

3.2. Криволинейный интеграл второго типа

Если Р(х,у) и Q(x,y) - непрерывные функции и гладкая кривая С, пробегаемая при изменении х от а до b, то соответствующий криволинейный интеграл второго типа выражается следующим образом:

В общем случае, когда кривая С задана параметрически: где t изменяется от до то имеем

Свойства криволинейного интеграла:

1. При перемене направления на кривой интегрирования криволинейный интеграл изменяет свой знак:

2. Кривую интегрирования можно разбить на две части:

3.

Криволинейный интеграл по замкнутой плоской линии при положитель­ном направлении обхода (против часовой стрелки) обозначается , а при

отрицательном направлении обхода обозначается

Вычисление криволинейного интеграла сводится к вычислению обыкновенного определённого интеграла: исходя из уравнения линии интегрирова­ния АВ подынтегральное выражение криволинейного интеграла преобразуется к одной переменной, значения которой в начале и в конце дуги АВ будут пре­делами полученного обыкновенного интеграла.

Пример 29. Вычислить криволинейный интеграл от точ­ки А(1;2) до точки В(0:2):

1) по прямой

2) по дуге параболы ;

3) по дуге эллипса

Решение.

1)

2)

3)