
- •Предисловие
- •1. Основные сведения об импульсных процессах
- •1.1. Импульсные режимы работы
- •1.2. Форма и параметры импульсов
- •1.3. Основные принципы генерирования мощных импульсов тока
- •1.4. Принципы построения зарядных устройств емкостных накопителей
- •2. Генераторы прямоугольных импульсов тока на основе реактивных формирующих двухполюсников
- •2.1. Переходные характеристики формирующих двухполюсников
- •2.2. Канонические схемы формирующих двухполюсников
- •2.3. Формирующие двухполюсники 1-го рода
- •2.4. Формирующие двухполюсники 2-го рода
- •2.5. Длинная линия в качестве формирующего двухполюсника
- •3. Генераторы импульсов тока на основе длинных линий
- •3.1. Волновые процессы в длинной линии
- •3.2. Согласование длинной линии и нагрузки
- •3.3. Однородная искусственная линия
- •3.4. Двойная длинная линия
- •3.5. Короткозамкнутая длинная линия, заряжаемая током
- •3.6. Коррекция формы импульсов
- •3.7. Работа однородной искусственной линии на комплексную нагрузку
- •3.8. Работа однородной искусственной линии на нелинейную нагрузку
- •3.9. Особенности расчета и проектирования генераторов на основе реактивных формирующих двухполюсников
- •4. Генераторы прямоугольных импульсов тока регулируемой длительности
- •4.1. Принципы построения генераторов импульсов регулируемой длительности
- •4.2. Частичный разряд емкостных накопителей
- •4.3. Частичный разряд эквивалентных формирующих двухполюсников
- •4.4. Энергетика процессов частичного разряда однородной искусственной линии
- •4.5. Длинная линия с распределенным диодом
- •4.6. Однородная искусственная линия с вентилями
- •4.7. Генераторы с дискретной регулировкой длительности импульсов
- •4.8. Особенности расчета и проектирования генераторов на основе однородных искусственных линий с вентилями
- •5. Генераторы импульсов тока регулируемой формы
- •5.1. Длинная линия с распределенным ключом
- •5.2. Теорема о соответствии формы эпюра зарядного напряжения длинной линии и формы импульса тока нагрузки
- •5.3. Длинная линия при одновременной коммутации распределенного ключа
- •5.4. Генераторы импульсов тока регулируемой формы на основе однородных искусственных линий
- •5.5. Генераторы импульсов тока регулируемой формы на основе расщепленных емкостных накопителей
- •5.6. Практическая реализация генераторов импульсов тока регулируемой формы
- •6. Зарядные устройства емкостных накопителей
- •6.1. Резистивный заряд емкостных накопителей
- •6.2. Индуктивный заряд емкостных накопителей
- •6.3. Управляемый резонансно-диодный заряд емкостных накопителей
- •6.4. Заряд емкостных накопителей от неуправляемых выпрямителей
- •6.5. Заряд емкостных накопителей от источников тока
- •6.6. Заряд расщепленных емкостных накопителей с помощью коммутатора зарядного тока
- •6.7. Энергетика процессов резистивного заряда расщепленных емкостных накопителей
- •6.8. Резонансно-диодный заряд расщепленных емкостных накопителей
- •Заключение
- •Список литературы
- •Оглавление
6.2. Индуктивный заряд емкостных накопителей
Эквивалентная схема цепи заряда при индуктивном заряде сосредоточенных емкостных накопителей или ФД приведена на рис. 6.5 [9]. Схема получена в предположении, что индуктивности ФД малы по сравнению с индуктивностью зарядного дросселя Lз, емкости конденсаторов отдельных ячеек ФД сосредоточены в емкости одного конденсатора С, а суммарные активные потери в цепи заряда определяются величиной резистора r. Уравнение баланса напряжений в зарядной цепи имеет вид
![]() ,
(6.4)
,
(6.4)
где q – мгновенное значение заряда емкости С.
П
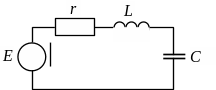 Рис.
6.5
Рис.
6.5
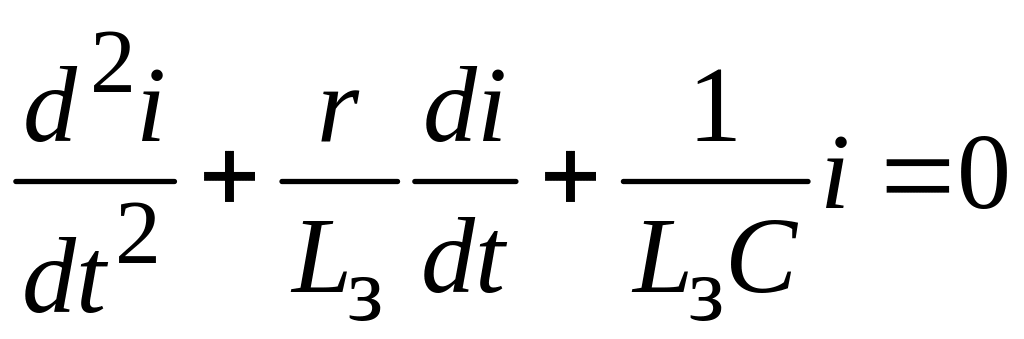 .
.
Приняв за начальные условия i = 0, uC = UC(0) при t = 0, получим решение этого уравнения в виде
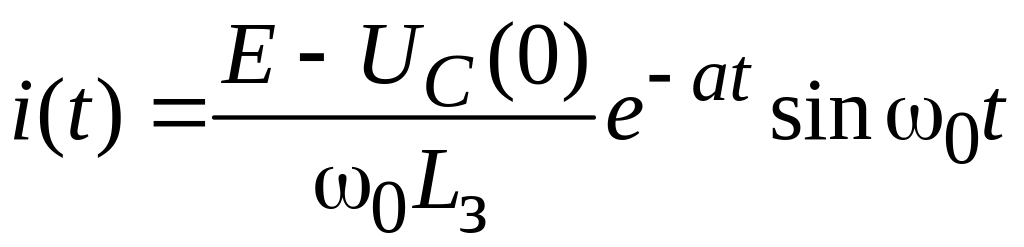 ,
,
где
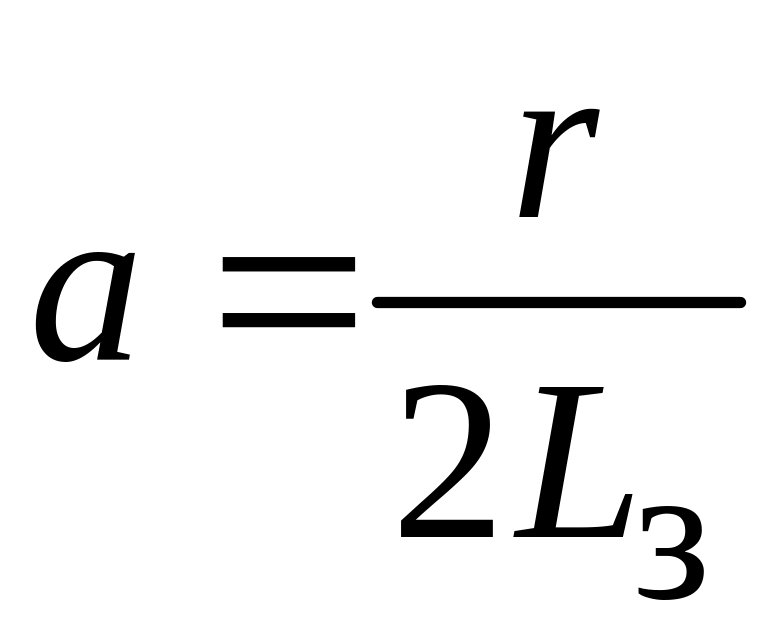 ;
;
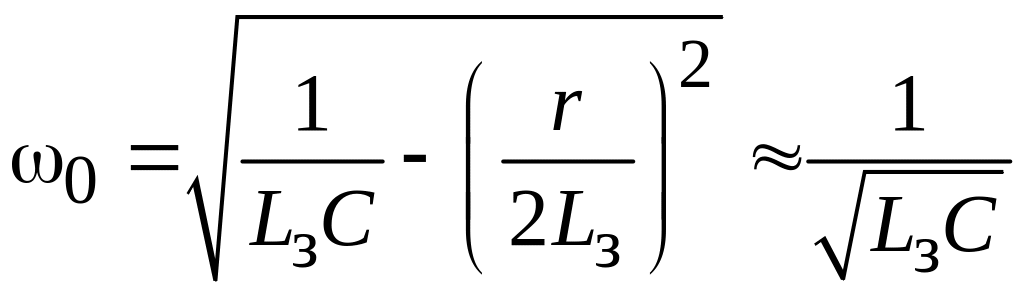 .
.
Для напряжения на накопителе получается зависимость
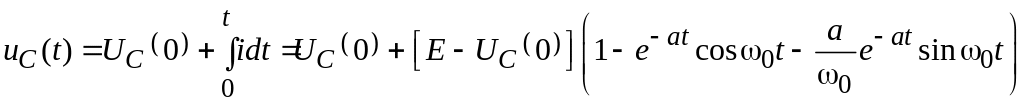 .
.
Временные зависимости тока заряда и
напряжения на накопителе от времени
для случая UC(0)
= 0 и
![]() приведены
на рис. 6.6. Заряд имеет медленно затухающий
колебательный характер с периодом
приведены
на рис. 6.6. Заряд имеет медленно затухающий
колебательный характер с периодом
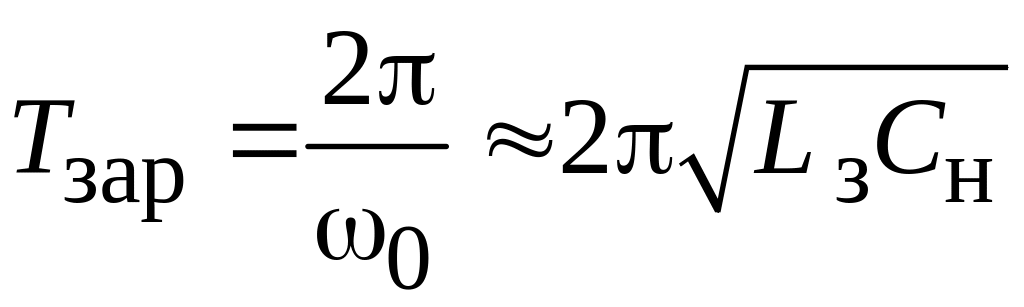 .
.
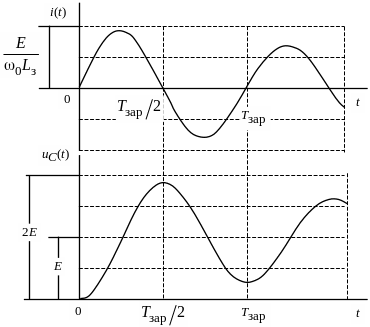 Рис.
6.6
Рис.
6.6
Через полпериода после начала зарядного процесса напряжение на накопителе достигает максимального значения, равного UCmax:
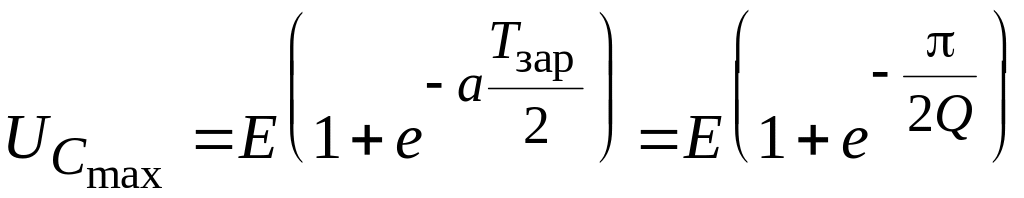 .
.
Здесь Q есть добротность зарядного контура:
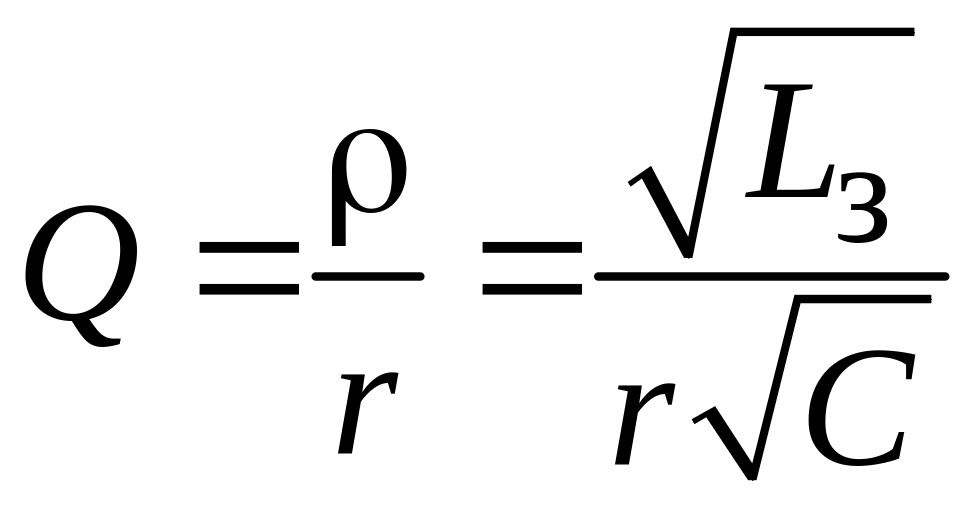 .
.
Поскольку на практике добротность может достигать достаточно больших величин (порядка 10…50), то в момент первого максимума напряжение на емкостном накопителе достигает почти двойного значения по сравнению с напряжением источника питания, т. е. Umax 2E. Это является существенным преимуществом перед другими видами заряда, так как позволяет применять источники питания с напряжением, почти вдвое меньшим того напряжения, которое должно быть получено на накопителе.
Для реализации этого преимущества разряд накопителя должен начинаться в момент максимума напряжения:
![]() ,
,
т. е. должно выполняться условие синхронизации:
![]() .
.
Отсюда вытекает условие для выбора значения зарядной индуктивности:
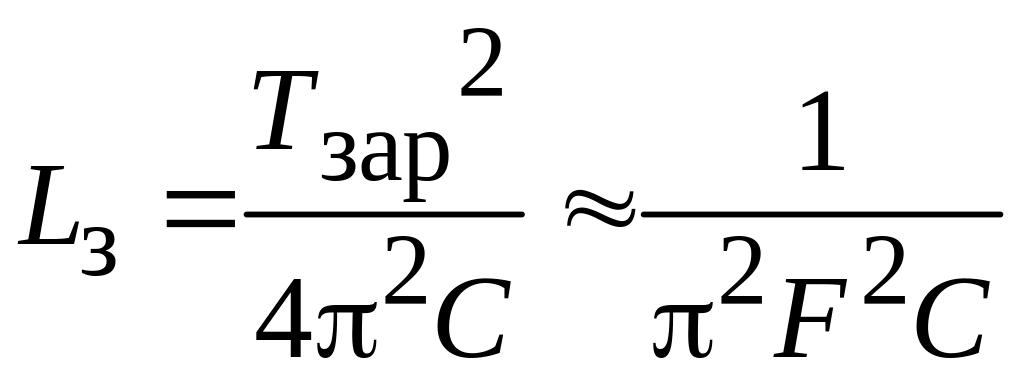 , (6.5)
, (6.5)
где F – частота следования импульсов тока нагрузки генератора, и период этой частоты равен T = 1/F. Рассмотренный режим заряда принято называть резонансным зарядом, для которого Тзар = 2Т.
На рис. 6.7 приведены зависимости напряжения накопителя и тока заряда от времени, причем временные интервалы представлены в относительных величинах.
Максимальное значение тока заряда
 ;
;
среднее значение этого тока
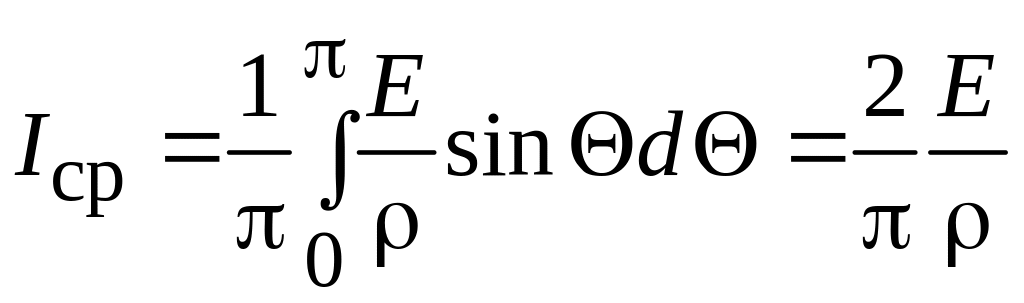 ;
;
действующее значение тока
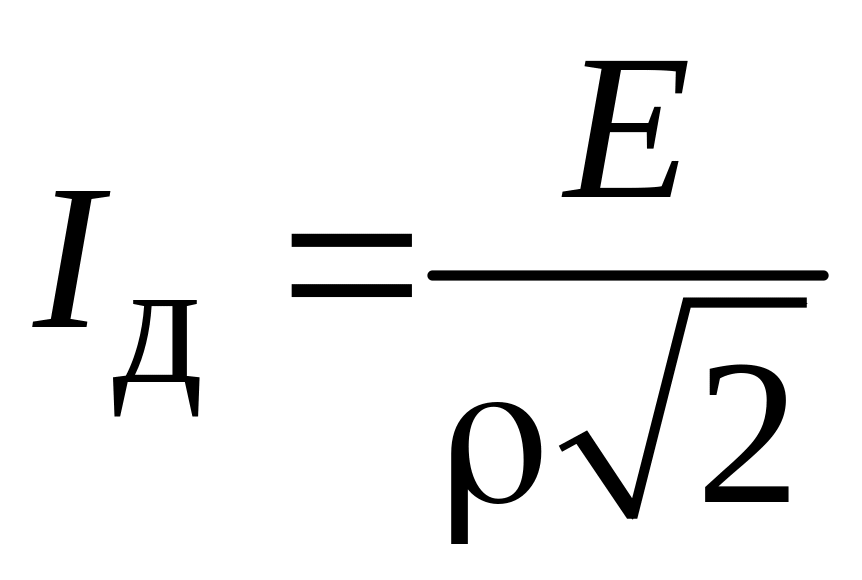 .
.
Указанные токи обычно сравниваются со
средним значением зарядного тока,
которое находится из простых соображений,
так как при согласованной нагрузке
![]() .
.
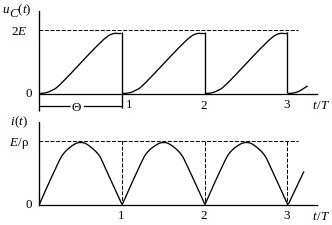 Рис.
6.7
Рис.
6.7
Характер заряда формирующей линии зависит от параметров зарядной цепи и частоты повторения импульсов, т. е. от режима работы генератора.
Другим видом заряда является так называемый линейный режим заряда. Он имеет место, когда
![]() ,
т. е.
,
т. е.
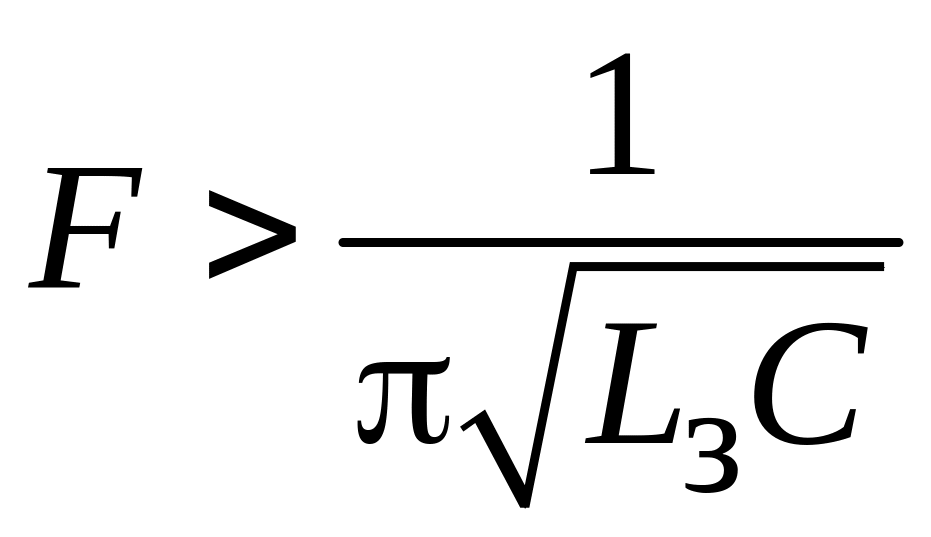 .
.
Для этого случая начальный зарядный ток I(0) 0 и для любого установившегося режима должен иметь определенное и постоянное значение. При отсутствии потерь в зарядном контуре и нулевом начальном заряде напряжение накопителя и зарядный ток имеют следующий вид:
![]() ; (6.6)
; (6.6)
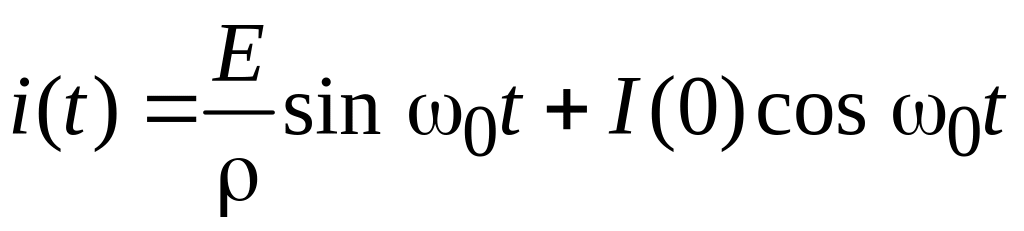 . (6.7)
. (6.7)
За тот короткий промежуток времени, в течение которого происходит разряд накопителя (формирующей линии), ток зарядного дросселя не успевает измениться, и поэтому зарядные токи в начале следующего и в конце предыдущего зарядных периодов равны, а при установившемся режиме равны также токи в начале и в конце данного периода, т. е.
I(0) = I(T). (6.8)
Принимая во внимание (6.8), из уравнения (6.7) можно найти начальный зарядный ток для установившегося режима:
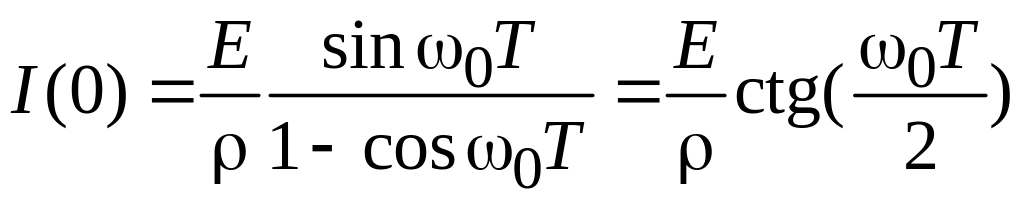 . (6.9)
. (6.9)
Из полученного уравнения видно, что
начальный зарядный ток может быть равен
нулю, если
![]() ,
больше нуля, если
,
больше нуля, если
![]() ,
и меньше нуля, если
,
и меньше нуля, если
![]() .
В зависимости от частоты работы генератора
кривая нарастания напряжения заряда
может иметь ту или иную форму, но к концу
периода заряда это напряжение всегда
будет равно удвоенному напряжению
источника питания, т. е.
.
В зависимости от частоты работы генератора
кривая нарастания напряжения заряда
может иметь ту или иную форму, но к концу
периода заряда это напряжение всегда
будет равно удвоенному напряжению
источника питания, т. е.
![]() .
Это легко доказывается подстановкой
I(0) из уравнения (6.9) в
уравнение (6.6).
.
Это легко доказывается подстановкой
I(0) из уравнения (6.9) в
уравнение (6.6).
На рис. 6.8 приведены зависимости напряжения и зарядного тока накопителя для линейного заряда.
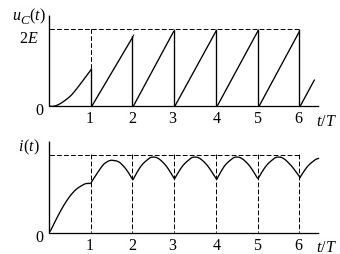 Рис.
6.8
Рис.
6.8
Кривые напряжения и тока представляют
собой определенные участки косинусоид
и синусоид, которые периодически
повторяются. Из рисунка видно, что кривая
напряжения накопителя почти приближается
к прямой линии. Это послужило основанием
назвать рассматриваемый вид заряда
линейным зарядом. Средний ток также
равен
,
а его действующее значение, аналитическое
вычисление которого связано с определенными
трудностями, уже при
![]() практически можно считать равным
среднему значению.
практически можно считать равным
среднему значению.
Рассмотрим третий вид заряда, при котором
![]() .
.
Н
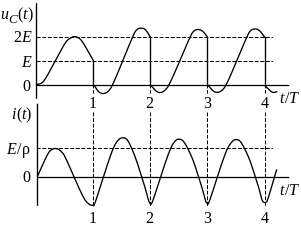 Рис.
6.9
Рис.
6.9
К
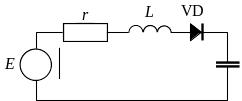 Рис.
6.10
Рис.
6.10
Последним видом заряда, нашедшем наиболее широкое применение на практике, является резонансно-диодный заряд (рис. 6.10) [7], [9]. В данном случае в зарядную цепь последовательно с дросселем включают вспомогательный диод, который не допускает обратного разряда накопителя в источник питания.
В связи с этим напряжение накопителя всегда будет удерживаться на максимальном уровне. Если не учитывать потери в цепи заряда и принять начальный ток заряда равным нулю, напряжение и ток накопителя могут быть найдены из зависимостей (6.6) и (6.7).
На рис. 6.11 приведены зависимости тока
и напряжения накопителя для случая
.
Из зависимостей (6.6) и (6.7) следует, что
напряжение заряда равно 2Е,
а ток заряда представляет собой
полусинусоиды, следующие друг за другом
с некоторым интервалом
![]() .
То, что напряжение заряда накопителя в
этом случае всегда равно 2Е,
может быть получено из следующих простых
соображений. В отсутствие потерь в
зарядной цепи энергия, приобретенная
накопителем за один цикл заряда, равна
энергии, потребленной от источника
питания, т. е.
.
То, что напряжение заряда накопителя в
этом случае всегда равно 2Е,
может быть получено из следующих простых
соображений. В отсутствие потерь в
зарядной цепи энергия, приобретенная
накопителем за один цикл заряда, равна
энергии, потребленной от источника
питания, т. е.
![]() ,
откуда
,
откуда
![]() .
.
 Рис.
6.11
Рис.
6.11
В случае резонансно-диодного заряда
имеется возможность в широких пределах
изменять рабочую частоту генератора.
При этом будет меняться длительность
паузы
![]() и
= 0
на максимальной частоте
и
= 0
на максимальной частоте
![]() .
Среднее значение тока заряда, знание
которого необходимо для выбора зарядного
диода, в этом случае
.
Среднее значение тока заряда, знание
которого необходимо для выбора зарядного
диода, в этом случае
![]() .
Действующее значение тока
.
Действующее значение тока
![]() .
В тех случаях, когда
.
В тех случаях, когда
![]() ,
т. е.
>0,
средний ток будет пропорционально
меньше, а действующее значение тока
,
т. е.
>0,
средний ток будет пропорционально
меньше, а действующее значение тока
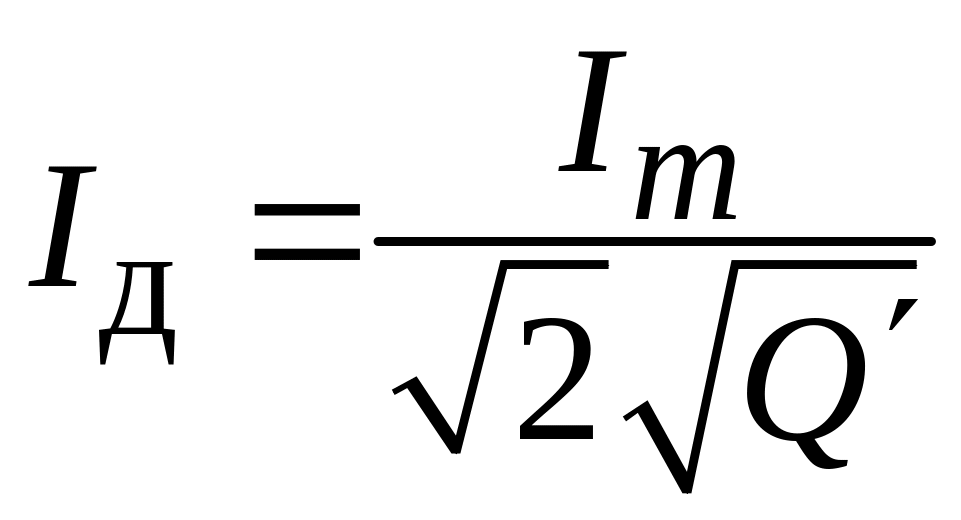 ,
,
где
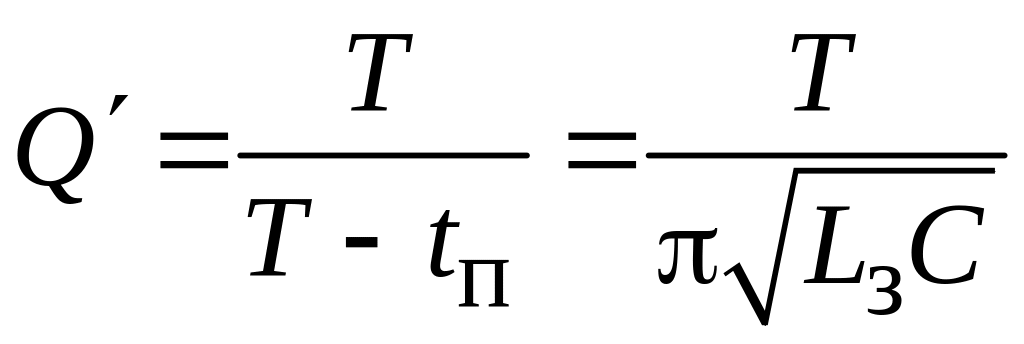 – скважность полусинусоидальных
импульсов зарядного тока.
– скважность полусинусоидальных
импульсов зарядного тока.
Определим КПД зарядного процесса при наличии потерь в зарядном контуре:
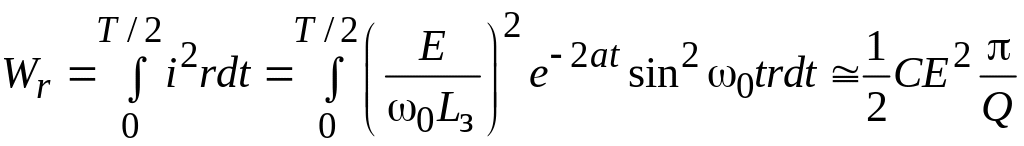 .
.
В этом случае Q =/r – добротность контура заряда.
Энергия накопителя
![]() .
.
Тогда
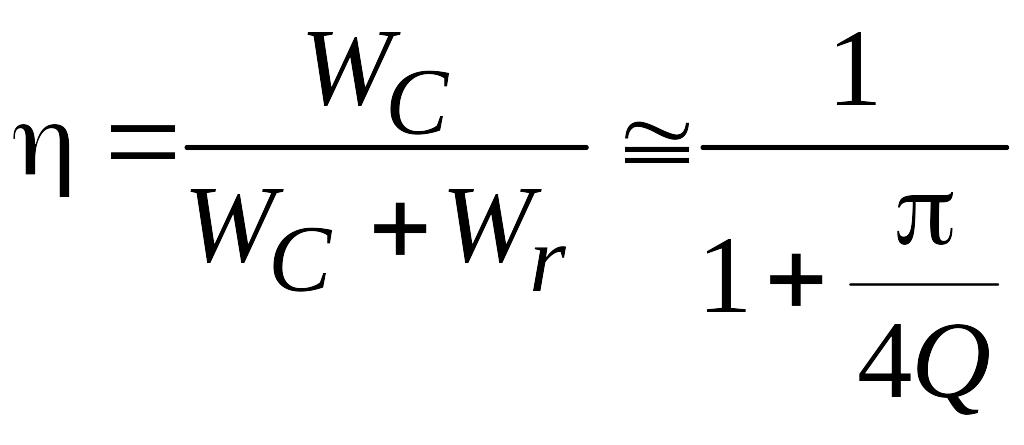 .
(6.10)
.
(6.10)
Из (6.10) следует, что 92 % уже при значениях Q = 10, т. е. КПД достигает достаточно высоких значений при величинах добротности, которые легко достигаются на практике. Тем не менее, абсолютно точный расчет КПД процесса заряда маловероятен в силу сложности учета всех потерь в элементах зарядного контура. Поэтому окончательное определение КПД обычно производится экспериментально на действующей установке. В данном случае удобно определить КПД как
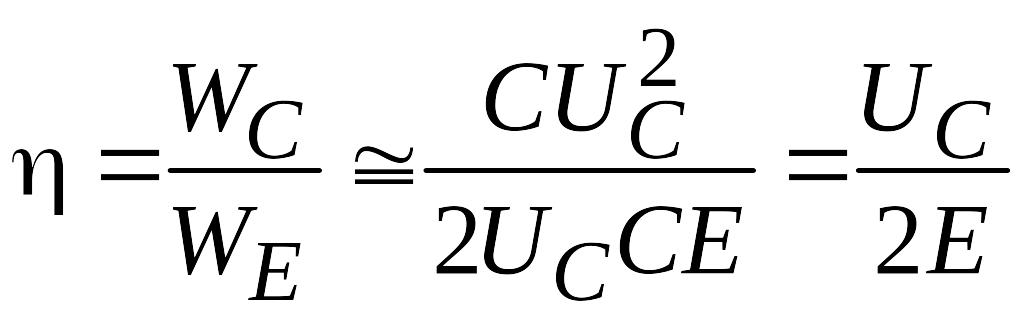 ,
(6.11)
,
(6.11)
где WE – энергия, потребленная от источника питания в процессе заряда. Из зависимости (6.11) следует, что для определения КПД достаточно замерить с помощью вольтметра, осциллографа или пикового вольтметра напряжение источника питания и максимальное напряжение на накопителе, что не представляет технических сложностей, а точность определения КПД будет высокой. Индуктивность при резонансно-диодном заряде определяется так же, как и для резонансного заряда при подстановке в (6.5) максимального значения рабочей частоты генератора .
Индуктивности, применяемые в таких зарядных устройствах, обычно выполняются с магнитопроводами. При рассмотрении режимов резонансно-диодного заряда емкостных накопителей, работающих при разряде на нелинейные и на нестационарные нагрузки, когда возникает возможность перезаряда накопителей, необходимо учитывать нелинейность зарядной индуктивности с магнитопроводом. При этом в литературе даются рекомендации по проектированию заведомо линейных индуктивностей с избыточным магнитопроводом. Аналитические или численные расчеты резонансно-диодного заряда при L = f(i) затруднительны и дают результаты только для частных случаев, что не позволяет сделать общие выводы для произвольной зависимости L = f(i). Но на самом деле этой проблемы не существует, и ответом на данный вопрос является следующая теорема [21].
Теорема 2. При резонансно-диодном заряде емкостного накопителя с ненулевым в общем случае начальным зарядом UC(0) и нелинейной зарядной индуктивностью L = f(i) напряжение заряда UC не зависит от вида нелинейности при отсутствии потерь в зарядном контуре.
Для доказательства этой теоремы используем закон сохранения энергии и примем условие, что UC(0) < E.
Энергия, запасенная в накопителе при окончании процесса заряда,
![]() (6.12)
(6.12)
Заряд, приобретенный накопителем,
q = C[UC – UC(0)].
Энергия, потребленная от источника ЭДС E за цикл заряда,
We = qE = CE[Uc – Uc(0)]. (6.13)
Так как потери в контуре отсутствуют, то We = Wc, и из (6.12) и (6.13) получим
![]()
откуда
Uc = 2E – Uc(0), (6.14)
что в точности соответствует процессу заряда в случае заведомо линейной индуктивности. Поскольку зависимость (6.14) получена без учета значения L = = f(i) и в ней исключено время как независимая переменная, теорема доказана.
