4.4. Энергетика процессов частичного разряда однородной искусственной линии

Доказанная в 4.3 теорема позволяет произвести количественную оценку энергетики процессов частичного разряда эквивалентных ФД на примере ОИЛ, которая при бесконечном числе звеньев является ЛРП. Рассмотрим два режима работы – на согласованную и на рассогласованную нагрузки.

При работе на согласованную нагрузку за время _к в нагрузке выделится энергия W_н = W₀^*, где ^* = _к/_max; 0  _к  _max. Начальная энергия ЛРП W₀ = 0,5q₀U₀.

Оставшаяся по завершении переходного процесса в линии энергия

W_ост = 0,5q_остU_ост. (4.12)

Значение остаточного заряда

q_ост = q₀(1 – ^*).

Отсюда U_ост = q_ост/C₀ = q₀(1 – ^*)/C₀ = U₀(1 – ^*). Тогда из (4.12) получим:

W_ост = 0,5q₀U₀(1 – ^*)².

Энергия потерь, рассеянная в линии в результате колебательного процесса при t > _к,

W_пот = W₀ – W_н – W_ост = 0,5q₀U₀(1 – ^*).^*

П

Рис. 4.8

ри этом КПД частичного разряда согласованной с нагрузкой линии  = 1/(2 – ^*). На рис. 4.8 приведены энергетические характеристики, где в относительных величинах представлены зависимости W^* = W/W₀ и КПД от относительной длительности импульса ^*. Анализ этих зависимостей позволяет сделать вывод, что частичный разряд согласованной с нагрузкой линии сопровождается значительными потерями энергии, которые максимальны при ^* = 0,5, когда энергия, запасенная в распределенной индуктивности линии, максимальна. КПД монотонно убывает от 100 % (^* = 1) до 50 % (^*  0), и практический интерес представляет толь­ко интервал регулирования длительности от 0,9^* до ^*, когда   90 %.

Покажем, что рассогласование линии с нагрузкой в сторону умень­шения волнового сопротивления линии позволяет повысить КПД генератора практически до любого заданного уровня.

Действительно, для формирования в одной и той же нагрузке R импульса тока с амплитудой I и максимальной длительностью _max парамет­ры рассогласованной ЛРП должны удовлетворять следующим условиям:

С₂ = _max/2 = _max/2R = C₁; L₂ = L₁/; U₀₂ = I(R + ) = U₀( + 1)/2,

где C₁, L₁, U₀ – емкость, индуктивность и напряжение заряда согласованной линии.

В нагрузке выделится энергия

W_н = I²R_max^*.

Начальное значение энергии рассогласованной линии

W₀₂ = C₂U²₀₂/2 = W₀( + 1)²/4 = I²R_max( + 1)²/4.

Остаточная энергия в рассогласованной линии W_ост2 определяется уров­нем остаточного напряжения U_ост2, которое найдем, используя закон сохранения заряда:

U_ост2 = q_ост2/C₂ = (q₀₂ – q_н2)/C₂ = IR( + 1 – 2^*)/,

где q₀₂ = C₂U₀₂ = C₂IR( + 1)/, q_н2 = I_max^* = 2IRC₂^*/.

Остаточная энергия

W_ост2 = С₂ U²_ост2/2 = I²R_max( + 1 – 2^*)²/4.

Отсюда КПД генератора на основе ЛРП, работающей в рассогласованном режиме,

₂ = W_н2/(W₀₂ – W_ост2) = /( + 1 – ^*).

На рис. 4.9 приведены зависимости  = f(^*) для различных значений коэффициента согласования , а на рис. 4.10 – зависимости КПД, напряжения заряда линии и энергии от .

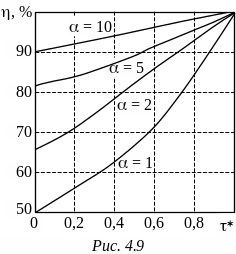
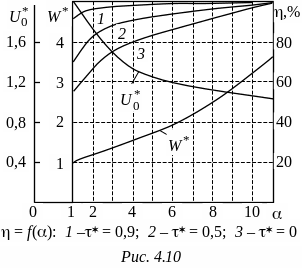
Анализ этих зависимостей позволяет сделать основной вывод о том, что рассогласование дает возможность существенно повысить КПД процесса частичного разряда и снизить значение зарядного напряжения линии при незначительном увеличении начальной энергии линии. Все изложенное справедливо и для ОИЛ с конечным числом элементов. При этом характер всех зависимостей сохраняется, а абсолютное значение отклонений всех величин не превышает 10 % уже при n = 4, уменьшаясь с ростом числа ячеек. Тем не менее несмотря на приемлемую энергетику частичного разряда рассогласованной линии практическая реализация таких генераторов существенно ограничивается из-за длительного переходного процесса в линии после отключения тока нагрузки, определяемого высокой добротностью реактивных элементов. Это резко снижает предельные значения рабочих частот данных генераторов, что в большинстве случаев неприемлемо. Выходом из указанной ситуации является техническое решение, описываемое далее.