17. Критерий Найквиста

Критерий Найквиста - частотный критерий позволяющий судить об устойчивости системы, замкнутой единичной отрицательной обратной связью, по виду амплитудно-фазовой характеристики разомкнутой системы. А.ф.ч.х. разомкнутой системы: K(jw) = A(w) + jB(w).

Формулировка критерия (для случая устойчивой разомкнутой системы): замкнутая система будет устойчивой, если а.ф.ч.х. устойчивой разомкнутой системы при изменении частоты w от 0 до ∞ не охватывает точку с координатами [-1, j0]

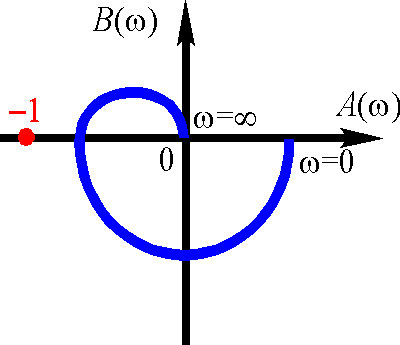
система устойчива

система на границе устойчивости

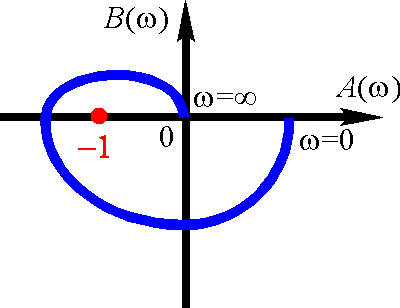
система не устойчива

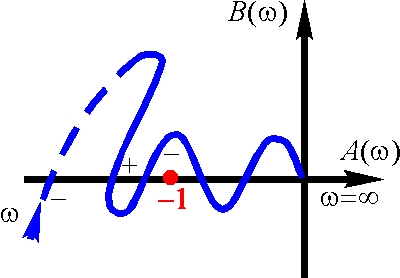
Можно воспользоваться другой формулировкой критерия Найквиста, основанной на подсчете количества положительных и отрицательных переходов характеристикой участка вещественной оси [-∞, -1].

Положительным переходом (при возрастании частоты w) называется переход а.ф.ч.х. разомкнутой системы участка [-∞, -1] из верхней полуплоскости в нижнюю.

Отрицательным - переход из нижней полуплоскости в верхнюю. Если w=0 а.ф.ч.х. разомкнутой системы начинается на отрезке [-∞, -1], то этому соответствует +1/2 или -1/2 перехода зависимости от того, вниз или вверх от этого отрезка идет а.ф.ч.х. при увеличении частоты.

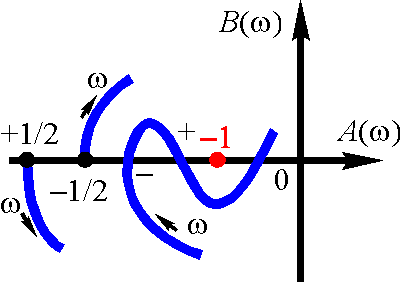
Вторая формулировка критерия Найквиста

Замкнутая система будет устойчивой, если разность между числом положительных и отрицательных переходов а.ф.ч.х. устойчивой разомкнутой системы через отрезок вещественной оси [-∞, -1] при изменении частоты от 0 до ∞ равна нулю.

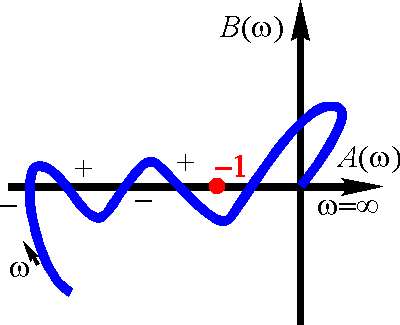
устойчивая система (замкнутая)

неустойчивая

18. Выделение областей устойчивости.

Одной из задач исследования систем автоматического регулирования и управления на устойчивость является определение некоторой области, в пределах которой могут изменятся те или иные параметры системы при сохранении ее устойчивости. Если система имеет q изменяемых параметров, то говорят о q-мерном пространстве параметров. Каждой точке этого пространства соответствуют характеристическое уравнение со своими значениями коэффициентов, а область пространства, внутри которой все значения параметров (или коэффициентов характеристического уравнения) соответствуют устойчивой системе, называется областью устойчивости. Гиперповерхность, ограничивающая эту область, называется граница области устойчивости. Если изменяемых коэффициентов (или параметров системы) два, то область устойчивости ограничена плоской кривой, если три, - то трехмерной поверхностью и т.д.

В принципе для выделения областей устойчивости могут быть использованы частотные критерии или критерий Гурвица. Однако, чтобы определить область устойчивости с помощью критериев Михайлова или Найквиста, нужно производить многократное построение соответствующих частотных характеристик. Если использовать критерий Гурвица, то решение задачи может оказаться связанным с анализом сложных и громоздких выражений или с построением кривых зависимостей определителя Гурвица от рассматриваемых параметров.

Наиболее удобно производить выделение областей устойчивости на основании понятия о D-разбиении, разработанного А.А. Соколовым и Ю.И. Неймарком. D-разбиением называется разбиение пространства коэффициентов характеристического уравнения (или параметров системы) на области, соответствующие одному и тому же числу корней, расположенных с лева от мнимой оси. Мнимая ось в плоскости корней характеристического уравнения есть отображение границы D-разбиения, и переход через последнюю в пространстве коэффициентов (или параметров) соответствует переходу корней в плоскости корней через мнимую ось.

Если характеристическое уравнение системы записано в виде

то для определения границы D-разбиения необходимо:

1. Найти уравнение границы в параметрической форме, заменив в рассматриваемом характеристическом полиноме "p" на "jw";

2. Получить границы искомых областей устойчивости, изменяя значения w от -∞ до ∞.

Если среди n корней рассматриваемого характеристического уравнения имеется k корней, лежащих в левой полуплоскости, и n - k корней, находящихся справа от мнимой оси, то построением D-разбиения будут выделены области из всех возможных сочетаний D(k, n-k). Хотя целью анализа является выделение только области устойчивости, т.е. области D(n, 0), построение всего D-разбиения обычно оказывается самым простым способом определения границы области устойчивости.

19. D-разбиение плоскости одного комплексного параметра.

Для построения границы D-разбиения по какому-нибудь одному параметру (коэффициенту преобразования, или постоянной времени, или моменту инерции и т.п.) необходимо:

1. Разрешить характеристическое уравнение относительно этого параметра, т.е. привести его к виду или

где l- параметр, значение которого меняется для обеспечения устойчивости.

2. Провести замену p на jw и отделить в полученном выражении действительную и мнимую части, т.е. свести его к виду

3. Откладывая по осям Re и Im соответствующие значения, построить кривую, которая получается, если частота w пробегает все значения от 0 до ∞.

4. Дополнить эту кривую ее зеркальным отображением относительно оси Re, т.е. ее ветвью, соответствующей -∞≤w≤0.

5. Двигаясь по полученной кривой от точки, соответствующей w=-∞, к точке, где w=∞, заштриховать левую ее сторону.

Штриховка кривой D-разбиения производится слева при изменении w от -∞ до +∞, что соответствует положению мнимой оси в координатной системе и расположению левых устойчивых корней. Итак устойчивая область (I) - область окруженная штриховкой. Отрезок AB область изменений параметра l для устойчивой САУ.

Для проверки в области устойчивости САУ берется любое значение на отрезке AB и одним из критериев осуществляется проверка факта устойчивости САУ.

Если при данной l САУ устойчива, то область I - область устойчивости.

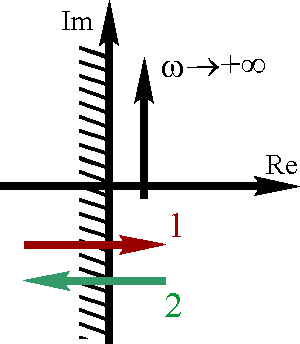
Граница D-разбиения - геометрическое расположение мнимой оси (Im) в плоскости одного параметра. Переходу корня в плоскости корней из штрихованной полуплоскости в нештрихованную вдоль стрелки 1 соответствует аналогичный переход через границу D-разбиения вдоль стрелки 1, и наоборот. Если пересекается область с двойной штриховкой (точка В), то в плоскости корней мнимую ось пересекает пара комплексно сопряженных корней.

Если известно количество правых корней, соответствующее хотя бы одной D-области, то двигаясь от нее через границы с учетом штриховок, можно обозначить все остальные области. Область с наибольшим количеством штриховок является претендентом на область устойчивости. Нужно взять любую точку из этой области и при соответствующем значении l проверить систему на устойчивость любым методом.

Есть одна особенность. Так как l - вещественное число, то jIm(jw) = 0, поэтому нас интересует не вся область устойчивости, а лишь отрезок вещественной оси в этой области, то есть l = Re(jw).

Если какой либо точке плоскости l соответствует характеристическое уравнение, имеющее k корней слева от мнимой оси, то такое же число корней слева имеет уравнение, соответствующее любой точке, в которой можно перейти, не пересекая границы D-разбиения. Если же при переходе к другой точке кривая пересекается с незаштрихованной стороны на заштрихованную, то этой новой точке соответствует характеристическое уравнение, имеющее слева от мнимой оси k+1 корней, если штриховка одинарная, и k+2 корней, если штриховка двойная (точки самопересечения кривой).

Таким образом, достаточно знать распределение корней относительно мнимой оси при каком-либо одном произвольном значении l, чтобы выяснить это распределение при любом другом значении l. Практический интерес представляет только действительные значения l. Поэтому, построив D-разбиение плоскости l и определив число корней, соответствующее каждой области, необходимо определить отрезок действительной оси, принадлежащей области устойчивости.

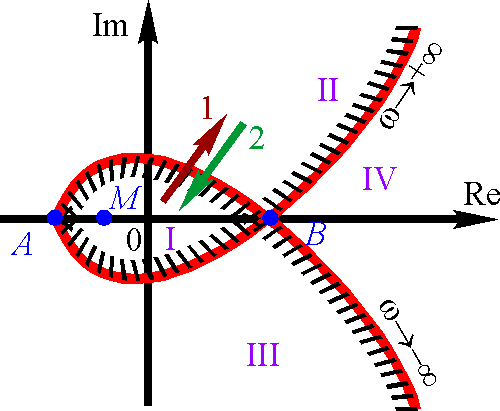
Итак годограф разбил комплексную плоскость на ряд областей I, II, III, IV. Если удается найти где-либо на плоскости точку (например M), соответствующую устойчивой системе, то следовательно, и вся область I есть область устойчивости.