11. Логарифмические частотные характеристики.

При практических расчетах автоматических систем удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называются логарифмическими. Они имеют меньшую кривизну и по этому могут быть приближенно заменены ломанными линиями, составленными из нескольких прямолинейных отрезков. Причем эти отрезки в большинстве случаев удается построить без громоздких вычислений по некоторым простым правила. Частоты, соответствующие точкам стыковки отрезков, называются сопрягающими и обозначаются w_c. Кроме того в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствуют сложение и вычитание ординат логарифмических характеристик.

12. Устойчивость линейных систем автоматического регулирования.

Понятие устойчивости системы автоматического регулирования связано со способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Наглядно устойчивость равновесия иллюстрируется на рис. 1, на котором изображен шар, лежащий в некотором углублении. При всяком отклонении его от положения равновесия он будет стремится возвратится к нему точно (при отсутствии сил трения) или в некоторой конечно области окружающей предшествующее положение равновесия (при наличии сил трения). Такое положение шара будет устойчивым.

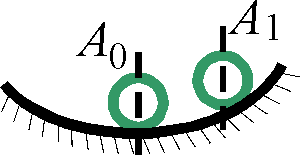
Рис. 1

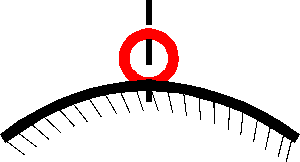
Рис. 2. Положение шара неустойчивое

Рис. 3. Безразличное положение равновесия

13. Необходимые и достаточные условия устойчивости.

Необходимые и достаточные условие устойчивости линеаризованных систем формулируются в теоремах А.М. Ляпунова.

Теорема 1: Если вещественные части всех корней p_i характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво, независимо от членов разложения выше первого порядка малости.

Теорема 2: Если среди корней p_i характеристического уравнения первого приближения найдется по меньшей мере один с положительной вещественной частью, то невозмущенное движение неустойчиво, независимо от членов разложения выше первого порядка малости

Обе теоремы позволяют исследовать все случаи из категории не критических, когда вопрос об устойчивости (или неустойчивости) невозмущенного движения однозначно разрешается на основе исследования уравнений первого приближения.

Если рассматривать линейную систему, то ее устойчивость определяется только структурой и параметрами, и не зависит от поступающих на систему сигналов. При этом стационарная линейная система (система с постоянными параметрами), описывается дифференциальным уравнением

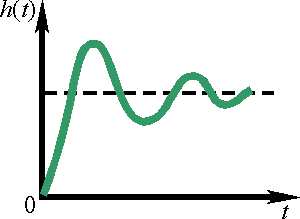
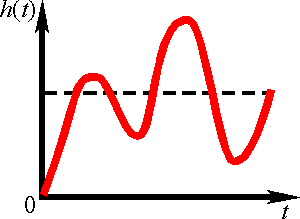
называется асимптотически устойчивой, если кривая, характеризующая ее свободное движение, затухает с течением времени, т.е. если где y _св(t) получается путем решения однородного дифференциального уравнения

Необходимым и достаточным условием устойчивости линейной стационарной системы при этом является отрицательность действительных частей всех корней ее характеристического уравнения

В геометрической интерпретации все корни характеристического уравнения должны находится в левой полуплоскости комплексной плоскости корней.

Система устойчива

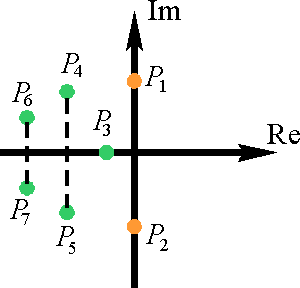
Система на границе устойчивости

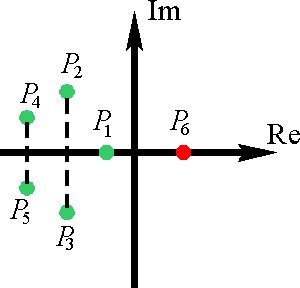
Система неустойчива

Так как при высоких порядках характеристических уравнений определение их корней представляет сложную задачу, то устойчивость реальных систем исследуют с помощью специально разработанных критериев.