Преобразование измерительных сигналов

Сигнал – материальный носитель информации, представляющий собой некий физический процесс, один из параметров которого непосредственно связан с измеряемой физической величиной. Этот параметр называется информативным.

Измерительный сигнал – сигнал, который обязательно дает количественную оценку измеряемой физической величине.

Классификация измерительных сигналов (ИС):

1. по характеру измерения во времени, может быть:

П остоянный сигнал – сигнал, который не изменяется во времени.

Переменный сигнал. В свою очередь который подразделяется на непрерывный

И мпульсный (колебания, действующие определенный конечный отрезок времени). Примером может служить радио и импульсы.

Жирным выделена видимая часть U_в(t).

U_p(t)=U_в(t)∙cos(ω₀t+ φ₀).

2. По характеру измерения информационного и временного параметра подразделяются на:

А налоговый – сигнал, описывающийся непрерывной или кусочно-непрерывной функцией.

Д искретный сигнал – сигнал, изменяющийся дискретно по времени. Описывается решетчатыми функциями.

Т – интервал дискретизации; n – целое число.

у_д(nT) Є (y_min; y_max) – интервал выборки.

Достоинства: нет необходимости поддерживать в течении какого–то времени, что дает возможность в организации многоканальной связи по одной линии (мультиплексирование каналов)

К вантовые сигналы – сигналы, квантованные по уровню.

h_i=n∙q, где q – квант; n – число квантов.

Ц ифровой сигнал – сигнал квантования по уровню и дискретизированный по времени.

у_ц (nT)=F_k (y_д (nT)) – функция квантования.

Для цифровых сигналов удобна система представления фиксированных значений в виде чисел. (Например: двоичная система исчисления). Для восьмиуровневого квантования необходим трёхразрядный двоичный код).

Число уровней квантования N и наименьшее число разрядов т двоичных чисел:

т=int(log₂N), где

int(А) – наименьшее целое число наименьшего число А.

С уменьшением кванта Δh увеличивается разрядность, уменьшается быстродействия передачи сигнала.

3. По степени наличия априорной информации о характере изменения ИС.

Детерминированные сигналы – определенные. Сигналы, мгновенное значение которых можно предсказать в любой момент времени.

Квадетерминированные – с частично известными параметрами.

Случайный – сигнал, поведение которого предсказать невозможно.

4. По размерности подразделяются

Одномерные

Многомерные

Виды детерминированных сигналов.

Элементарные:

П остоянные;

Е диничная функция. Функция Хевисайа.

Д искретное представление

д ельта – функция (импульс)

Д искетная S – функция:

Стробируя непрерывный сигнал, мы получаем дискретный. Процесс стробирования записывается:

если непрерывную функцию умножить на S(t-t₀) и проинтегрировать по времени, то результат будет равен мгновенному значению непрерывной функции в точке t₀, где сосредоточен импульс.

Структурная модель выглядит следующим образом:

И деальный дискретный сигнал:

где у(k∆T) – значение непрерывного сигнала в k-ом шаге дискретизации.

Гармонический сигнал. Моногармоническими сигналами считаются сигналы, изменяющиеся во времени, согласно функциям sin и соs. Все остальные сигналы – полигармонические, так как состоят из множества гармоническими составляющими с разными частотами.

у(t)=y_m∙sin(ωt+ φ₀), где

y_m – пиковое значение;

Т – период времени;

φ₀ – начальная фаза.

Сложные сигналы:

П рямоугольный импульс.

у(t)=y_m∙[1-(t-t₀)- 1-(t-t₀-τ)], где

τ – длительность импульса.

q – скважность импульса (q=T/τ). Если q=2, то последовательность импульсов называется меандром.

Т рапецевидный импульс.

τ_с обычно больше, чем τ_н.

Измерительные сигналы с линейными участками нарастания – пилообразные сигналы.

а ) однополярные

б ) знакопеременные

К сложным измерительным сигналам относится любой модулированный сигнал.

Г оворя о детерминированных сигналах, их подразделяют на периодические и непериодические.

Периодические сигналы – сигналы, значения которых повторяется через определенные интервалы времени. Периодический сигнал может содержать одну гармонику. А может много – полигармонический сигнал. Поэтому для описания периодических сигналов часто используют спектральное (частотное) представление, используя преобразование Фурье. Периодический сигнал часто характеризуется спектром. Используя преобразование Фурье.

где

А _п и φ_п – амплитуда и фаза п-ой­ гармоники соответственно. Множество А_п – амплитудный спектр. Множество φ_п составляет фазовый спектр. А₀ - постоянная составляющая.

Линейчатый амплитудный спектр выглядит следующим образом:

Интегральные параметры:

Среднее значение постоянной составляющей:

Средневыпрямленное значение:

Среднеквадратичное (действительное) значение:

Непериодические сигналы:

Спектральная функция:

- спектральная плотность.

По размерности подразделяются:

Одномерный сигнал х(t);

Многомерный сигнал V(х₁(t), х₂(t),…).

Линейное пространство сигналов

S₁(t)… S_n(t) М

Если они взаимосвязаны, то говорят о существовании пространства сигналов. Чтобы М было вещественно–линейным пространством необходимо выполнение ряда аксиом:

1. U M, то U принимает только вещественные значения.

2. U, V M существует сумма W=U+V₁ M

U≠V=V+U

(U+V)+x=(U+x)+V

3. S M, α

f=S ∙ α M

4. Ø M, U+Ø=U

Все эти аксиомы справедливы как для аналоговых, так и для цифровых сигналов. В любом линейном пространстве найдется подмножество Е={l₁…l_n}, которое выполняет роль координатных осей координатный базис.

, где с_i – число проекции измеряемого сигнала на координатный базис.

Норма сигнала – количественная оценка вектора.

║S║ - норма.

Линейное пространство М называют нормированным, если каждому S(t) M соответствует число ║S║ и выполняется следующая аксиома:

1. ║S║>0

2. α ║S║∙ α=║S ∙α║

3. Если существует S(t), Р(t) M и их нормы, то выполняется неравенство треугольника.

║S+р║≤║S║+║р║

Энергия сигнала определяется как квадрат нормы сигнала. Важная характеристика, так как о величине сигнала часто судят по его энергетическому эффекту. С другой стороны энергетическая норма мало чувствительна к изменению формы сигнала.

.

Метрика. Характеризует расстояние между сигналами. Линейное пространство называется метрическим, если каждой паре элементов U, V M соответствует неотрицательное число β, характеризующее расстояние между ними и выполняются следующие аксиомы:

1. Рефлексивность β(U, V)= β(V, U)

2. β(U, U)=0

3. β(U, V)≤ β(U, W)+ β(W, V), M

Существует связь между нормой и метрикой:

β(U, U)=║U- V║ - метрика это норма разности двух сигналов.

║U║= β(U, Ø) – норма сигнала U тождественна расстоянию межу U и нулевым элементом.

Разложение сигнала по ортонормированным базисам

Запишем энергию суммы двух сигналов:

Последнее слагаемое буде представлять собой взаимную энергию.

- взаимная энергия

;

- скалярное произведение.

Два сигнала называются ортогональными, если их скалярное произведение равно нулю.

Предположим, то в некотором пространстве сигналов задана система ненулевых функций φ₀(x)… φ_n(x), причем выполняется на конечном отрезке [a,b] условия:

1. Функции должны быть ортогональными, то есть

, п≠т.

[a,b] – интервал ортогональности.

2. Функции должны иметь единичную норму:

При выполнении данных условий говорят, что система функций {φ_n(х)} ортонормированна.

Система нормированных функций, каждая из которых попарно ортогональна, называется ортонормированной.

Доказано, если в линейном пространстве сигналов существуют φ₁(t), φ₂(t)… φ_n(t) и эта система функций является нормируемой, то любую кусочно-непрерывную функцию f(x) можно разложить в ряд Фурье, если оно удовлетворяет условиям Дирихле:

- обобщенный ряд Фурье, где

- i-ый коэффициент ряда Фурье, так как необходимо.

, .

На геометрическом языке. С_i – ‘j проекция исследуемого сигнала на ортонормируемый базис.

.

Представление сигнала по ортогональному базису называется обобщенным рядом Фурье. Коэффициентами такого рода служат скалярные произведения разлагаемого сигнала и соответствующих базисных векторов.

Основные свойства ряда Фурье.

При заданной системе функций φ_n(х) и фиксированном числе слагаемых ряда, он обеспечивает наилучшую аппроксимацию исследуемого сигнала, то есть линейные значения среднеквадратичного отклонения.

,

.

Ортогональная система называется полной, если увеличение числа коэффициентов ряда позволяет среднюю квадратическую ошибку μ сколь угодно малой.

Все слагаемые, кроме i=j будут равны нулю, поэтому:

.

Энергия сигнала – сумма энергий всех компонент, из которых складывается ряд Фурье.

Аппаратное реализация разложение сигналов.

Примеры ортонормированных базисов.

Выбор наиболее лучшей (рациональной) ортонормированной системы функций зависит от цели преследуемой при разложении сложной функции в ряд.

Существуют 2 направления:

1. разложение на простейшие функции = системы тригонометрических функций синусов и косинусов:

   • гармонические колебания являются простейшей функцией, неподлежащей дальнейшим разложениям в спектр;

   • гармонические колебания являются единственной функцией времени, сохраняющее свою форму при прохождении через любую механическую систему.

2. аппроксимация сигналов, когда требуется свести к минимуму число членов ряда при заданной допустимой погрешности.

Применяются: полиномы Чебышева, Лаггера, функции Уолша и Хагра.

Преобразование Лаггера.

Полиномы Лаггера удобны ля разложения функций, имеющих в своём составе экспоненциальную составляющую.

, при х>0, где

х – информационный параметр;

п – степень полинома.

.

Ортометрический базис Уолша (для дискретных сигналов).

Существует на отрезке [-Т/2; Т/2] (Т – период дискретизации), и обладает следующими свойствами:

1. принимает два значения: 1 и -1.

2. любые две функции Уолша ортогональны.

3. функция Уолша периодическая с периодом равным 1.

wal(x) θ=T/2

Проверка базиса Уолша на:

1. ортогональность:

2. нормируемость:

Разложение сигнала по функции Уолша выглядит:

.

Разложение сигналов по элементарным базисам

Спектральное разложение сигналов по тригонометрическим базисам.

Совокупность коэффициентов ряда Фурье в базисе тригонометрических функций – частотный спектр периодического сигнала.

Для разложения в ряд Фурье тригонометрическая базисная функция, описывающая измерительный сигнал (ИС), должна быть: периодической, интегрируемой, а так же не обращаться в бесконечность при разрывах.

Используется следующий набор функций:

1, cosωt, sinωt, cos2ωt, sin2ωt.

;

.

Если S(t) чётное, то , если S(t) нечётное, то .

Каждую гармонику можно охарактеризовать амплитудой и фазой. Тогда форма измерительного сигнала в тригонометрическом базисе выглядит следующим образом:

,

,

;

Комплексная форма записи.

Ряд Фурье может быть представлен в комплексной форме, если базисные функции записать в виде экспонент с мнимыми показателями.

.

Интегральное преобразование Фурье.

Гармонический анализ периодических сигналов можно распространить и на непериодические сигналы.

0<t<T (ω=2πT)

.

Для перехода к предельному непериодическому сигналу необходим устремить Т→∞.

При Т→∞:

1. ω→dω

2. n∙ω→ω

3. сумма→dω

.

Формула обратного преобразования Фурье выглядит следующим образом:

.

Основные свойства преобразования Фурье:

1. линейность: S₁(t)→ S₁(ω)… S_n(t)→ S_n(ω)

2. преобразование Фурье сигнала, смещенного во времени

S (t)↔ S (ω); S(t-t₀); S’(ω)-?

│x=t-t₀│

3. преобразование Фурье производной сигнала

S (t)↔ S (ω);

F(ω)-?

F(ω)=jωS(ω).

Для n-ой производной F(ω)=(jω)²S(ω).

4. преобразование Фурье произведения сигналов

U(t)↔ U (ω); V(t)↔ V(ω);

Сверка спектральных плотностей:

.

Произведению сигналов соответствуют спектральная плотность, пропорциональная свертке этих сигналов.

Данная теорема имеет обратную силу:

U(ω), V(ω);

U (ω)∙V(ω)↔V(t)×U(t).

Произведению спектральных плотностей U(ω) и V(ω) соответствует свертка сигналов.

.

Спектральная плотность измерительного сигнала есть характеристика частоты. Является комплексно-значимой характеристикой, несущей информацию и об амплитуде и о фазе измерительного сигнала.

Спектральная плотность обладает всеми свойствами спектральных коэффициентов с отличием в Ом, что в спектре непериодического сигнала присутствуют все частоты. Формулу для S(ω) называют прямым преобразованием Фурье.

Условие наличия спектральной плотности у сигналов:

1. δ(t) (при t=0, δ(t)=∞, при t≠0, δ(t)=0)

S(t)=A∙δ(t),

t=0; S(ω)=A∙e⁰=A

2. прямоугольный импульс.

τ _и­ - длительность импульса.

; ; S(ξ=0)=Uτ_u.

3. экспоненциальный видеоимпульс

S(t)=U∙e^-αtδ(t).

.

; ;

; .

Для описания интегрированной плотности неинтегрируемых сигналов вводится понятие обобщенной спектральной плотности. Для этого рассматривают дополнительную функцию, которая является абсолютно интегрируемой и имеет спектральную плотность S(ω) и связана с исследуемым сигналом формулой Релея:

1. постоянный сигнал.

U(t)=A, V(t), V(ω)

.

Используя фильтрующие свойства δ – функции, получим U(ω)=2π∙A∙δ(ω).

Чем шире временной сигнал, тем уже спектральная плотность.

2. 

Вывод: чем больше длительность импульса, тем меньше ширина его спектра. Это важно для определения частотного диапазона аппаратуры, обрабатывающей сигнал (ей надо обеспечить широкую полосу пропускания).

Дискретизация аналоговых сигналов. Дискретное преобразование Фурье.

Аналоговый сигнал:

;

t_k=k∙Δ (Δ – шаг дискретизации, k=0, ±1, ±2…).

Дискретизированный сигнал:

.

t_пр – время, необходимое АЦП для преобразования мгновенного значения U_c в цифровые данные.

Устройство выборки значений дискретизированного аналогового сигнала.

Ключ k₂ замкнут.

Спектральную плотность дискретизированного сигнала, состоящая из N отсчетов:

ω=n∙Δω.

- дискретное преобразование Фурье (ДПФ)

ω→n∙Δω.

kT→k

(n=0, ±1, ±2…± N/2) – алгоритм вычисления спектральных коэффициентов по временным отсчетам S(k).

{S[n]}; {S[k]}.

(k =0, 1, 2… N-1).

Теорема Котельникова

Непрерывный сигнал, спектр которого не содержит частот больше f_m, может быть однозначно представлен мгновенными значениями (выборками), разделенными одинаковыми интервалами времени, длина которых не должна превышать Т<1/2∙f_m.

Дискретный сигнал:

Ω - частота поступления импульсов.

Спектр дискретного сигнала есть множественное повторение спектра аналоговых сигналов, следующих с частотой F=1/T.

Спектр цифрового сигнала:

S_T(ω)= S_T(Δω∙n)

Δω∙N=ω

ω= Δω∙n

- прямое преобразование Фурье. Позволяет по заданным временным отсчетам S[k] вычислять спектральные коэффициенты S[п].

Обратное преобразование Фурье:

(n=0, ±1, ±2…± N-1).

Свойства ДПФ и ОДПФ:

1. Линейность:

S1[k]	S2[k]
S1[п]	S2[п]

ДПФ

2. Нулевой коэффициент S [0] есть постоянная составляющая и является средним значением всех отсчетов.

3. Если S [k] действительные отсчеты и N – четное, то в данном случае имеет место симметричность сигнала:

4. Свертка дискретных сигналов:

S [k]	g[k]
S [п]	G[п]

(k =0, ±1, ±2… ±N-1).

ДПФ сигналов, отображающих циклическую свертку отсчетов, равно произведению спектральных плотностей соответствующих сигналов.

Быстрое преобразование Фурье (БПФ). Суть его заключается в нахождении в ДПФ и ОДПФ массивов с меньшим числом членов. В MathCAD БПФ находится функцией fft(v).

Преобразование сигналов.

1. Преобразование, изменяющее частоту и фазу сигнала:

U₁=U₀sinωt

U₂=U₀sin(n∙ωt)

2. Преобразование, связанное с уменьшением мощности сигнала. Это прохождение сигнала через усилитель мощности, сумматоры мощностей.

3. Преобразование, связанное с модуляцией. Модуляция – процесс управления одним или несколькими параметрами колебаний высшей частоты в соответствии с законом передаваемого сообщения.

При модуляции происходит процесс наложения передаваемого сообщения на другое колебание – несущее, f_нк>f_nc.

4. Преобразование сигналов, связанное с фильтрацией. Процесс фильтрации заключается в выделении полезных составляющий спектра и в подавлении шумовых.

5. Преобразование, связанное с демодуляцией – выделение принятого сообщения из модулированного колебания.

6. Преобразование, связанное с обработкой сигналов. Комплекс преобразований в приемнике сигналов, направленный на улучшение правильной идентификации полезного сигнала на фоне помех согласно выбранному критерию, называют обработкой сигналов.

Амплитудная модуляция сигналов.

Модуляция дает возможность организации многоканальной связи по одной линии передачи. Выбор несущей частоты позволит повлиять на дальность передачи информационного сообщения. Передаваемый сигнал называют модулирующим. Несущее количество называют модулируемым.

При амплитудной модуляции, в соответствии с законом передаваемого сообщения, меняется амплитуда модулируемого сигнала. При этом частота и фаза постоянны.

Однотональная модуляция возможна, если модулирующий сигнал представлен периодической функцией:

S(t)=U_mcosΩt

Ω - частота распространения.

U_н(t)=U₀ cosω₀t

ω₀ – частота распространения несущего колебания.

Рассмотрим случай Ω>>ω₀:

U (t)=U₀ (1+т∙cosΩt)cosω₀t

m – модуль (индекс) модуляции

U_огиб=U₀ (1+т∙S(t))

U(t)=U₀ cosω₀t+½∙m∙U₀∙cos(ω₀-Ω)t+½∙m∙U₀∙cos(ω₀+Ω)t

Д иапазон спектра равен 2Ω

Ширина спектра амплитудно–модулированного сигнала равна удвоенному значению наивысшей частоты в спектре модулированного сигнала.

Однополосная модуляция (SSB).

Балансная амплитудная модуляция (DSBSC):

Данный вид модуляции широко используется для создания высокочастотных радиотелефонных каналов. Особенность приема SSB – сигнала заключается в наличии умножающего детектора, чтобы опять получить исчезнувшую несущую частоту.

Схемы генерации амплитудно-модулированных сигналов.

Простейшая схема генерации амлитуно-модулированных сигналов выглядит следующим образом:

А мплитудой сигнала управляют напряжением высокочастотного усилителя. Закон управления должен быть линейным.

При отсутствии модулированного сигнала транзистор VT1 (высокочастотный) смещен в активную область и работает в качестве усилителя ВЧ несущего колебания. Дроссель DR1 препятствует закорачиванию высокочастотной энергии на источник питания. Конденсатор С₁ служит развязкой межу генератором модуляционного сигнала и источником питания. Конденсатор С₂ согласует выходное сопротивление каскада и антенны А. Под действием модулирующего сигнала напряжения на коллекторе транзистора изменяется в соответствии с законом модулирующего сигнала, происходит положение на несущее колебание.

Детектирование амплитудно-модулированных сигналов.

Извлечение информации из модулированного радиочастотного сигнала основано на детектировании. Схема детектирования выглядит следующим образом:

Н аведенный высокочастотный сигнал в антенне трансформируется в контуре L₁, L₂, C. Причем контур L₂C настроен в резонанс с несущей частотой ω₀. Таким образом, высокочастотный сигнал резко возрастает в амплитуде. Основой детекторной схемы служит диод VD1 и высокочастотный фильтр С_фR_ф. В качестве диодов рекомендуется использовать диоды Шоттки, так как у них минимальная зона нечувствительности.

U_кр=0.8 B

U_гер=0.4 B

Диод выпрямляется высокочастотный сигнал, отсекая нижнюю составляющую. Продетектированный сигнал проходит на фильтр низких частот. Ввиду малого комплексного сопряжения конденсатора к ВЧ сигналам. ВЧ сигнал закорачивается на землю, а в усилитель НЧ на VT2 проходит верхняя огибающая, несущая информацию, где усиливаются до необходимого уровня.

Недостатки данного типа схемы:

1. относительная дороговизна VT1 и VT2;

2. необходимость точного согласования одновременно настраиваемых LC контуров;

3. затруднено применение пьезофильтров с крутыми фронтами ПП, что обычно очень желательно.

Решению этих проблем способствует применение гетеродинного приемника.

Б лок – схема:

1 – резонансный ВЧ усилитель;

2 – гетеродин (локальный генератор, который настроен на определенную частоту)

3,5 – усилители промежуточной частоты;

4 – пьезоэлектрический фильтр;

6 – детектор с НЧ фильтром;

7 – усилитель низких частот.

Поступающий сигнал усиливается одним каскадом ВЧ усилителя и смешивается с сигналом гетеродина. Получается сигнал фиксированной промежуточной частоты. Сигнал такой частоты удобен для дальнейших преобразований. Далее следует набор резонансных усилителей с фиксированной настройкой на ПЧ, и содержащих такие селективные элементы, как пьезофильтры. Схема заканчивается детектором и усилителем звуковых частот. Настройка данного приемника происходит за счет изменения частоты гетеродина Аким образом, чтобы при смешении любой входной частоты получалась фиксированная ПЧ, на которой усиление и чувствительность максимальна. Необходима настройка ВЧ усилителя с генератором гетеродином.

Диапазон АМ [0.06-30] МГц.

Угловая модуляция

Частотно – и фазомодулированные сигналы получаю при изменении в несущем гармоническом сигнале либо частоты ω, либо начальные фазы φ₀. При этом амплитуда остается постоянной.

U_H(t)=U₀cos(ω₀t+ φ₀);

A= U₀=const.

ψ=ωt+φ₀ – полная фаза ВЧ колебаний.

Изменение мгновенной частоты ω определяется при частотной модуляции:

ω= ω₀+Δω_д ∙cosΩt, где

Δω_д – девиация частоты, отражающая изменение частоты у несущей в зависимости от амплитуды модулирующего сигнала.

Частотная модуляция:

Δω_д=k∙U_m;

S(t)= U₀∙cosΩt;

ψ(t)= ω₀+Δω_д ∙cosΩ+φ₀;

Δφ_д=k∙U_m;

где

т – индекс частотной или, в общем случае, угловой модуляции.

.

Фазовая модуляция:

Оба вида модуляции изменяют как мгновенную частоту, так и фазу модулирующего сигнала. Однако параметры Δφ_д и Δω_д по-разному зависят от частоты модулирующего сигнала Ω.

Частотная модуляция:

Ф азовая модуляция:

Спектры частотной и фазовой модуляции.

1. m<<1

- узкополосный частотно-модулированный спектр.

2. m>>1. Увеличивая число боковых составляющих спектра на частотах, кратных модулирующей частоте Ω.

, где

I_k – функция Бесселя, определяющая амплитуду частотных составляющих.

Чем больше т, тем больше спектр.

Δf_сп=2∙Δω_д+2∙Ω=2(m+1) ∙Ω, при m>>1, Δf_сп≈2∙Δω_д.

При увеличении т происходит перераспределение мощности. При определенном значении т можно добиться, что ω₀=0, и вся мощность сосредоточиться на боковых составляющих.

Диапазон частотной модуляции (88÷108) МГц – УКВ.

Преимущества ЧМ перед АМ:

большая помехоустойчивость;

высокое качество передачи.

Частотную модуляцию применяют для передачи звукового сопровождения телевизионных программ.

Схемы частотной и фазовой модуляции могут быть прямые и косвенные.

При ЧМ прямым методом происходит непосредственное воздействие на автогенератор, выдающий колебания с определенной частотой.

При ФМ прямым методом воздействия на ВЧ усилитель, определяющий фазу колебаний:

Из ФМ можно получить ЧМ, ведя интегратор:

ФМ косвенным методом: вводится дифференцирующая цепочка и на выхде получаем ФМ:

Схемы частотной модуляции.

Наиболее часто применяют ЧМ на основе варикапа (полупроводникового диода с обратно смещенным р-п-переходом).

Частотная модуляция прямым способом:

Делитель на R₁, R₂ обеспечивает активную область транзистора VT1 в режиме ВЧ усилителя. Контур L₁C₁C₂ образует положительную обратную связь, в результате чего транзисторный каскад преобразуется в автогенератор с частотой f₀ (частота автогенератора при отсутствии информационного сигнала).

Модулирующий сигнал U_m, несущий информацию, трансформируясь через транзистор, изменяет ёмкость варикапа VD1, в результате чего изменяется частота автогенератора.

U_m~C_VD1~f_Г.

Выходной сигнал представляет собой падение напряжения ВЧ дросселя ДP1.

Схемы модуляции ЧМ и ФМ.

АО – амплитудный ограничитель (ограничивает сигнал по U_m);

ПФПЧ – полосовой фильтр промежуточной частоты (f_сп=2(Δω+F_m));

ЧД – частотный детектор.

Принципиальная схема ЧД.

Описывают на расстроенных LC – контурах.

Декор ЧМ сигнала основан на конуре LC, расстроенном на диапазон Δf относительно f₀.

Принцип работы заключается в преобразовании частотной модуляции в амплитудную.

При изменении частоты входного сигнала происходит изменение сопротивления LC – контура и соответственно амплитуды выходного сигнала. Данное схемное решение обладает не лучшей линейной зависимостью рабочих характеристик.

Детектор отношений – комбинация двух амплитудных детекторов.

f_р1>f₀

f_р2<f₀

U_вых=F(U_m, Q, Δf_p).

, при f₀ U_вых=0

U_вых= U_q1- U_q2

Напряжение на выходе детекторов U_q1 и U_q2 определяется резонансными характеристиками контуров.

Выходное напряжение есть разность U_q1 и U_q2 - функция, зависящая от амплитуды модулирующего сигнала.

Изменяя значение добротностей контуров и расстроенную Δf_р, можно регулировать крутизну и протяженность линейного участка характеристики.

Модуляция цифровых сообщений

Импульсная модуляция.

ШИМ – широтно-импульсная модуляция;

ФИМ – фазовая импульсная модуляция (сдвиг фаз).

Модуляция цифровых сообщений.

Фазовая модуляция характеризуется дискретом фазы Δφ. В зависимости от выбора Δφ различают бинарную (BPSK) квадратурную манипуляцию. Бинарная фазовая модуляция позволяет различать единичный бит информации (1 или 0).

Основное преимущество заключается в том, что на несущей частое спектральная составляющая отсутствует и вся энергия концентрируется в боковых составляющих.

Недостаток: небольшой объем передаваемой информации.

Для увеличения объема применяют квадратурную фазовую модуляцию (QPSK).

Фазовая модуляция позволяет различать информацию из двух битов информации:

Δφ=π/2; φ₀=0; π/2; π; 3π/2

11	0
01	π/2
10	π
00	3π/2

С целью улучшения различия одного символа от другого используют относительную квадратурную фазовую манипуляцию(ОQPSK).

Δφ=π/2

11	π/4
01	π/2+π/4=3π/4
10	5π/4
00	7π/4

Частотная модуляция.

Применяют двухступенчатую манипуляцию. Добиваются сужения частотной полосы пропускания. Структурная схема двухступенчатой манипуляции выглядит следующим образом:

На вход первой ступени поступает цифровое сообщение (1 или 0). В процессе работы 1 присваивается F₁, а 0 присваивается F₂.

F₁=M∙F_T

, где τ – длительность одного импульса.

F₁=N∙F_T

M, N – числа, показывающие сколько периодов частоты под несущей укладывается внутри элементарной посылки.

F₀=0,5(F₁+F₂)

ΔF=F₁-F₂

F₁= F₀ +0,5ΔF

F₂= F₀ -0,5ΔF

Во второй ступени сигнал под несущей модулирует частоту под несущей радиопередатчика (используется схема с варикапом).

, где Δf_Д – девиация частоты второй ступени.

Критерии выбора F₁ и F₂:

1. выбирают более плавный фазовый переход от F₁ к F_2­;

2. энергетический спектр промодулированного сигнала должен быть сконцентрирован в довольно узкой полосе.

Для сохранения непрерывности фазы через каждые 2 бита осуществляется дополнительный поворот фазы на π.

, где

F – частота следования меандра (ПП=4F).

При частотной модуляции и при квадратурной фазовой модуляции, можно попарно передавать биты, используя четыре значения частоты: F₁, F₂, F₃, F₄.

Демодуляция манипулированных сигналов.

1. Частотный детектор

При f₁>f₀ сигнал проходи через верхнюю цепочку. Напряжение на нагрузке U=+U₀.

При f₁<f₀ напряжение на нагрузке U=-U₀.

Цифровой частотный компаратор:

2. фазовый детектор основан не перемножении двух сигналов.

U_C=U₁cos∙(ωt+φ)

U_Г=U₂cosωt

U_вых=U_Дcosφ

U_Г=±U_Д – при изменении фазы от 0 до π.

Пороговый элемент на ОУ:

Структурная схема при двухступенчатой частотной демодуляции:

ЧД – 2 – пороговый элемент.

На первом этапе демодуляции выделяется частота поднесущей. На втором – исходное информационное сообщение.

U_Д=U₀cos(2πF₁t) – «1»

U_Д=U₀cos(2πF₁t) – «0»

Импульсная модуляция – это модуляция колебаний, в результате которой гармонические колебания приобретают вид кратковременных радиоимпульсов, характеристики которых определяются формой модулирующего колебания.

Импульсная модуляция широко применяется в радиолокации. При этом передаваемый сигнал может изменять различные параметры исходящей последовательности радиоприемников. Если высоту, то получаем амплитудную ИМ, если частоту – ЧИМ, смещение импульсов во времени без изменения длительности импульсов – ФИМ.

Схема импульсного модулятора:

ПИЭ – первичный источник энергии;

НЭ – накопительный элемент (могут быть емкостные, индуктивные, смешанные);

КЭ – коммутирующий элемент (жесткого и мягкого типа);

СВЧ-Г – СВЧ – генератор.

Так как скважность приходящих радиоимпульсов большая, есть возможность накаливать энергию в паузе между импульсами, что понижает мощность ПИЭ.

Схема модулятора жесткого типа с емкостным накопителем:

1 фаза:

при отсутствии импульса транзистор VT1 закрыт отрицательным напряжением на базе. Происходит заряд конденсатора по экспоненциальному закону:

U_C=E_0∙ (1-e^-t/T3)

T₃=(R₁+R₂)C.

2 фаза:

Приходит положительный импульс, который открывает VT1 и происходит разряд конденсатора через СВЧ – генератор:

U_C=E_0∙ e^-t/Tр

T_р=(R_кл+R_ген)C.

R_кл – сопротивление ключа (отрицательное).

Диод VD1 необходим ля того, чтобы гасить колебания, возникающие при коммутации больших токов.

Линейно-частотная модуляция (ЛЧМ).

ЛЧМ отличается от обычных радиоимпульсов ем, что ВЧ заполнение имеет переменную частоту, изменяющуюся по линейному закону:

,

где Т – длительность ЛЧМ сигнала

.

Свойства ЛЧМ сигнала – возможность сжатия его во времени. Устройство сжатия осуществляет задержку сигнала, подаваемого на вход, причем время задержки уменьшается с увеличением частоты проходящего сигнала. Произойдет сжатие и на выходе устройства задержки одновременно появятся ВЧ и НЧ составляющие сигнала.

Это свойство применяется в радиолокации. Позволяет повысить точность в определении дальности объекта без ухудшения точности.

Фильтрация

Фильтрация – это любое преобразование измерительных сигналов с целью изменения соотношения их спектральных составляющих.

При фильтрации решаются две основные задачи:

1. выделение полезного сигнала на фоне помех;

2. спектральный анализ.

Классификация фильтрации:

• По роду преобразований:

  1. аналоговая;

  2. цифровая.

• По расположению полосы пропускания (ПП):

1. низкочастотная;

2. высокочастотная;

3. полосовая;

4. заграждающая (режекторная).

Фильтр низких частот: Фильтр высоких частот:

Полосовой фильтр: Заграждающий фильтр:

По типу использования динамических систем:

1. линейная;

2. нелинейная.

Линейная фильтрация используется чаще, так как любой измерительный сигнал может быть представлен математической моделью случайный гауссовых процессов, для которых линейная фильтрация обеспечивает возможность выделения информативного сигнала на фоне помех.

Нелинейная фильтрация используется для подавления импульсных помех.

По устройству или физическому принципу работы фильтры различают:

1. реактивные сосредоточенного типа (L, C). Рабочий диапазон ограничен до 300 МГц.

2. реактивные распределенного типа (волноводы, лини с распределенными параметрами). Рабочий диапазон свыше 300 МГц.

3. кристаллические (используется пьезоэффект). Достоинства таких фильтров – это высокая добротность цепи и высокая стабильность, так как электрические параметры кристалла мало завися от времени и температуры изменений. Рабочий диапазон частот ограничивается технологическими возможностями на стадии изготовления – от 1 кГц до 500 кГц.

4. Активные (сроятся на основе операционных усилителей). Рабочий диапазон частот– от 0 до 500 кГц.

5. цифровые (на основе цифровой техники и микропроцессоров).

Основные характеристики фильтров:

, где

п – порядок фильтра.

p=j∙ω

h(t) – импульсная характеристика.

Из формулы видно, что частотный коэффициент передачи фильтра связан с его импульсной характеристикой через преобразование Фурье:

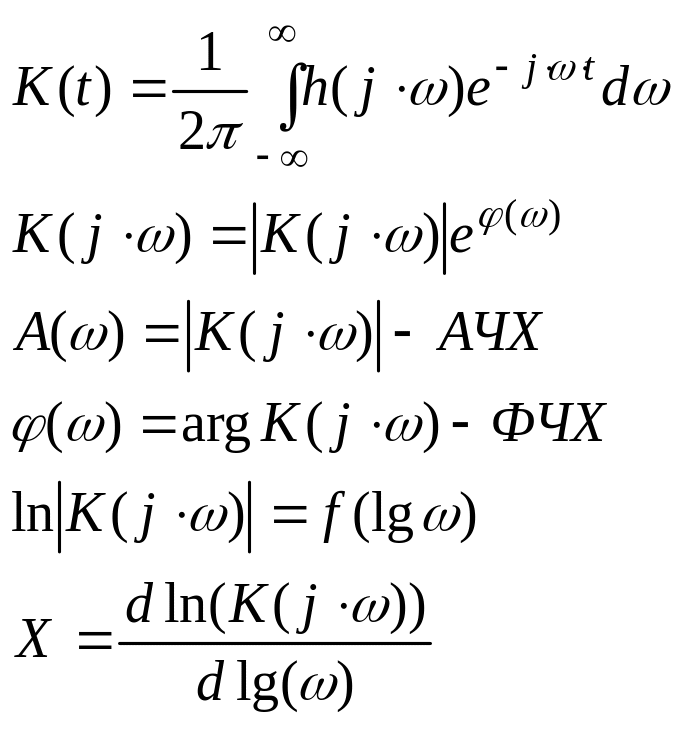
где Х – крутизна АЧХ – величина, не зависящая от масштаба координат и измеряется в дБ/дек, если изменение частоты происходит в 10 раз, и в дБ/октаву, если в 2 раза.

Фильтры могут быть физически реализуемые и физически неосуществимые. Для физической реализации фильтров необходимо выполнение условий:

1. принцип казуальности:

h(t)>0, t≤0.

Выходной сигнал не может возникнуть до момента появления импульса на входе.

2. правило устойчивости:

Импульсная характеристика должна быть абсолютно интегрируемой:

Практически это выражено затуханием h(t).

t→∞; h(t)→0. Корни характеристического уравнения передаточной функции лежат в левой полуплоскости.

3. критерий Пэли – Винера:

.

Из этого условия вытекает, что физически осуществимыми буду те фильтры, у которых АЧХ не имеет нулевых значений в некоторой полосе пропускания.

Физически неосуществимые фильтры называют математическими. Они в основном используются для анализа.

Любой фильтр выполняет функцию согласования. Эта функция сводится к трансформации одного сопротивления в другое, при которой выполняется условие отбора от источника максимальной мощности в определенной области частот.

- КП по мощности.

Коэффициент затухания по мощности:

в₃=-10lg(K_P).

П ри идеальном согласовании К_Р=1; в₃=0. Это достигается за счет равенства z_i и z_вх.

У идеальных фильтров АЧХ имеет следующий вид (крутизна АЧХ=∞):

Реальный фильтр всегда характеризуется переходной областью между ПП и ПЗ, и крутизна АЧХ конечна. Кроме того, присутствует пульсирование в ПП и ПЗ. Для описания реальных фильтров используется идеализированная АЧХ – ассимпот.

Крутизна падения амплитуды зависит от порядка фильтров. Реальная частота среза ω_ср(р) соответствует уравнению затухания, равному – 3 дБ.

Алгоритм синтеза фильтров.

1. Выбор идеализированной функции, которая описывает требуемую характеристику затухания фильтра. Такой фильтр физически нереальный.

2. Аппроксимация такой функцией, которая делает фильтр физически реализуемым.

3. По аппроксимирующей частотной характеристике находят передаточную функцию фильтра и работают с ней.

4. зная расположение нулей и полюсов осуществляют принципиальную реализацию фильтров.

Методы апроксимации идеализированных характеристик на примере ФНЧ.

1. Апроксимация Батерворта (максимально плоская апроксимация).

, где - нормированная частота; п – порядок фильтра.

ω_Н >>1

K_P(ω_Н)≈ ω_Н ^-2n

Δ ≈ -20∙logω_Н

Достоинства: простота реализации, отсутствие колебаний.

Недостаток: достаточно раннее снижение амплитуды (ещё в ПП):