Федеральное государственное образовательное
учреждение высшего профессионального образования
«Южный федеральный университет»
Махно В.И., Коваленко Е.В.
Учебно-методическое пособие для организации самостоятельной работы студентов физического факультета по разделу «Молекулярная физика». Модули VII – IX.
Ростов-на-Дону
2008
|
Махно В.И., Коваленко Е.В. |
|
Учебно-методическое пособие для организации самостоятельной работы студентов физического факультета по разделу «Молекулярная физика». Модули VII-IX. Ростов-на-Дону, 2008. 20 с. |
Учебно-методическое пособие предназначено для организации самостоятельной работы студентов по курсу «Молекулярная физика», читаемому по программе общей физики для студентов первого курса очного обучения физического факультета ЮФУ. Изложенный теоретический материал, проектные и тестовые задания помогут усвоению основ статистической физики, знание которых необходимо для применения в некоторых разделах, изучаемых в «Молекулярной физике» на первом курсе физического факультета ЮФУ.
Введение
Опыт работы со студентами первого курса физического факультета показывает, что важное место в учебном процессе занимает самостоятельная работа студентов, организация которой связана с преодолением ряда затруднений. Одно из них заключается в том, что математическая подготовка нынешних первокурсников оказывается недостаточной для эффективной самостоятельной работы даже над материалом стандартных, рекомендованных программой, учебников. Это ощущается уже при изложении некоторых разделов механики в первом семестре. Но особенно это сказывается при изложении молекулярной физики и термодинамики во втором семестре первого курса.
Для решения этой проблемы можно бы излагать этот материал на четвертом или пятом курсах, что и реализуется в некоторых зарубежных университетах; при этом отмеченные математические проблемы исчезают, преподавание молекулярной физики ведется с привлечением мощного аппарата квантовой физики и теории вероятностей. Но при этом, как отмечается во многих аналитических работах, посвященных анализу этой методики, исчезает суть общей физики, она превращается в чрезвычайно теоретизированный раздел, по сути дела, в самый математизированный раздел теоретической физики. Таким образом, внешне хорошая методическая идея, уводя от одной проблемы, приводит к другой крайности.
В принятой в России программе изложения курса общей физики её разделы являются фундаментом для понимания курса теоретической физики. Это достигается построением физических моделей явлений, их качественным анализом с последующим переходом к количественному.
В свете изложенного становится понятным появление различных методических разработок, направленных на поиск путей решения указанной проблемы приемами, адекватными ситуации, складывающейся в вузах в связи с пересмотром учебных программ в средних школах как в области физики, так и в области элементарной математики, а также негативными веяниями демографического кризиса на конкурсную ситуацию в вузы Ростовской области.
В разработанном учебно-методическом пособии предлагается один из путей облегчения понимания студентами некоторых трудно усваиваемых разделов курса молекулярной физики как одной из частей курса общей физики.
Научное обоснование методики организации самостоятельной работы студентов над курсом «Молекулярная физика»
В принятой в России программе изложения курса общей физики её разделы являются фундаментом для понимания курса теоретической физики. Это достигается построением физических моделей явлений, их качественным анализом с последующим переходом к количественным расчетам. При этом уже в курсе общей физики появляются сложные понятия из теоретической физики.
В свете интернационализации образования и перехода к использованию Болонских принципов в организации учебного процесса в последнее время важная роль отводится управляемой самостоятельной работе студентов, использованию проектных методов, расширению тьюторских возможностей. Для успешного решения таких задач необходимо проведение крупномасштабных работ по созданию качественного методического обеспечения курсов лекций, семинарских и практических занятий. Несмотря на наличие большого количества учебников, работа по созданию авторских методических разработок необходима, так как появляется возможность предложить методически более приемлемое, облегченное изложение отдельных разделов, представляющих большую трудность для усвоения, собрать воедино разбросанные по различным источникам полезные сведения, важную информацию, что существенно дополнит курс лекций.
В свете вышеизложенного для создания учебно-методической связки, обеспечивающей успешный переход от общей физики на первом курсе к теоретической на третьем, в разработанном учебно-методическом пособии выделены модули, в которых предложена методика отработки основных понятий, связанных со статистическими распределениями, которые являются неотъемлемой частью курса общей физики и основой статистической физики. Доступное изложение теоретического материала достигается некоторым снижением математической строгости, что учитывает пониженный уровень математической подготовки современных первокурсников.
Для облегчения работы учебный материал разбит на три теоретических модуля с максимально компактным и логически доступным изложением вопросов, вызывающих затруднения как на лекционном уровне, так и при самостоятельном изучении раздела, посвященного основам статистической физики. Закреплению теоретического материала способствует выполнение предлагаемых к каждому модулю проектных заданий и проработка тестовых заданий. Для выполнения части проектных заданий требуется проработать некоторые рекомендованные литературные источники.
МОДУЛЬ VII. Распределение Больцмана
Цель модуля – изложить главное содержание функции распределения частиц по энергиям, увязывая вводимые понятия с их вероятностным смыслом, на котором базируется статистическая физика. При этом студент имеет возможность выяснить границы применимости классических соотношений, их отличие от квантовых. Более глубокое понимание изложенного материала достигается при выполнении проектных и тестовых заданий, проведение которых предполагается организовать в режиме тьюторинга.
Под термодинамическим равновесием понимается такое состояние системы, которое наступает при отсутствии внешнего воздействия, при этом параметры системы не меняют своих значений и в системе не происходит макроскопических изменений.
Пусть система, находящаяся в
термодинамическом равновесии, состоит
из N одинаковых частиц.
Вследствие теплового движения и
взаимодействия частиц энергии отдельных
частиц с течением времени изменяются,
но полная энергия остаётся постоянной.
Возможные значения энергии разобьём
на интервалы так, что в пределах
энергетического интервала энергия
непрерывно меняется от
до
.
Условно изобразим ось энергий и
энергетические интервалы. Пусть число
частиц, приходящихся на i-й
энергетический интервал, в среднем
равно
.
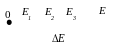
Частицы, находящиеся на i-м
интервале, имеют энергию
.
Энергию системы частиц можно представить
в виде:
(1)
Доля частиц, приходящаяся на i-й
интервал, равна
и является вероятностной характеристикой.
В состоянии термодинамического равновесия
доля частиц i-го
интервала
должна быть функцией энергии; разные
i-е интервалы, в
общем случае, имеют разные
энергии и заполнены различным числом
частиц
(2)
Функция
называется функцией распределения
частиц по энергиям,
.
В статистической физике доказывается, что
(3)
где А – постоянная величина, k – постоянная Больцмана.
Число частиц, имеющих энергию в интервале
от
до
в потенциальном силовом поле, определяется
величиной
.
Так как
– полному числу частиц в системе, то
, (4)
откуда
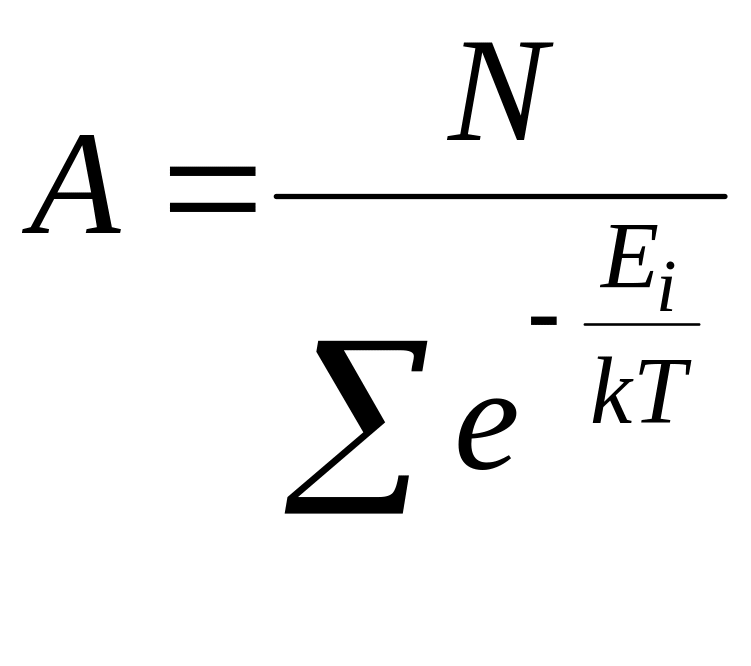(5)
Подставим (5) в (3):
.
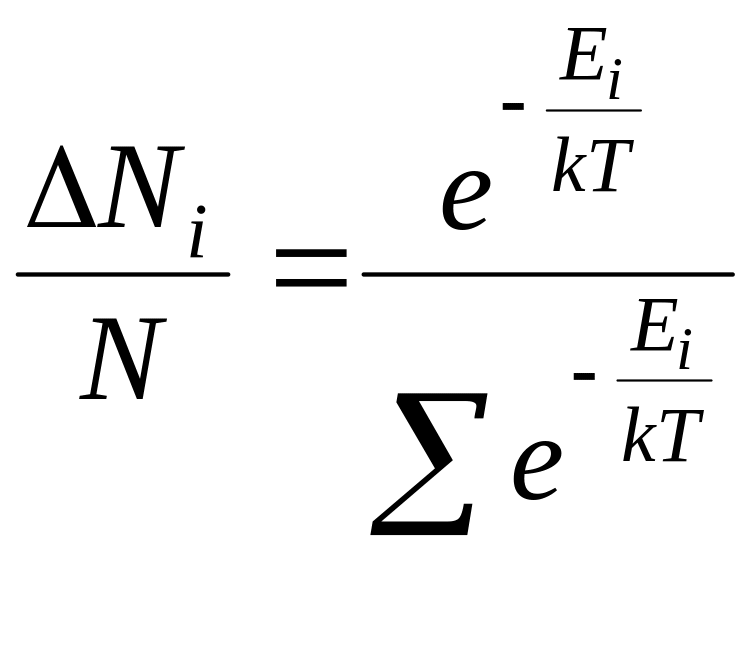(6)
Выражение (6) определяет вероятность заполнения частицами i-го энергетического уровня.
Разделим (6) на
:
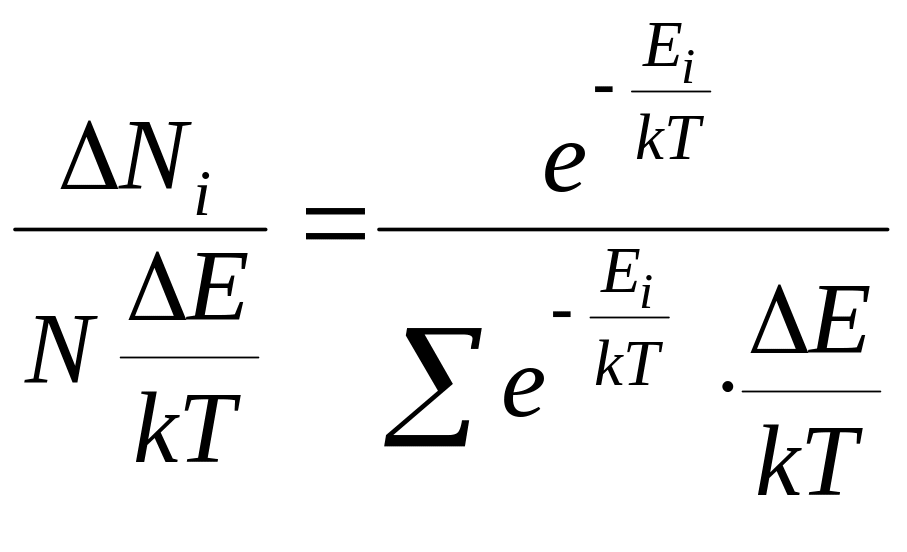(7)
– безразмерный интервал энергии,
измеряемой в единицах
;
величина, входящая в левую часть равенства
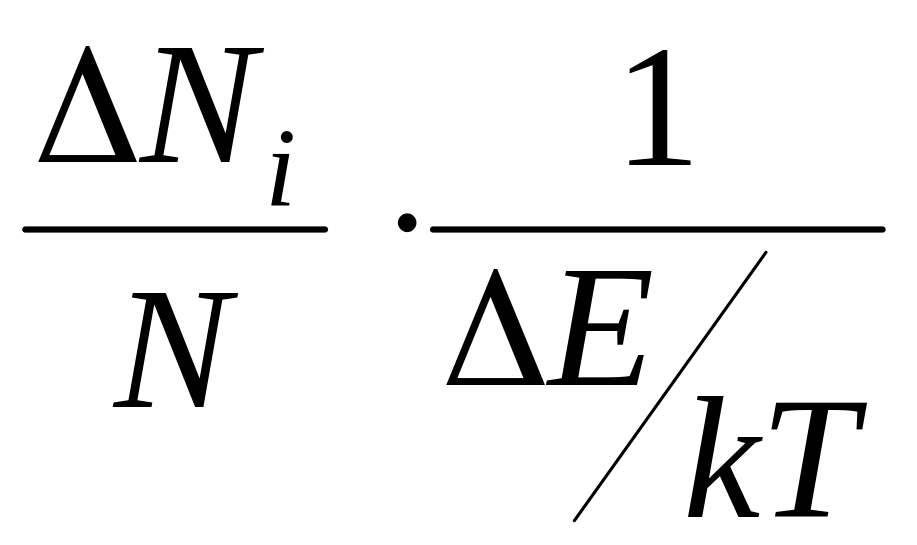(8)
называется плотность вероятности, т.е.
вероятность нахождения молекул в
единичном безразмерном энергетическом
интервале (
,
+1).
В пределе получим:
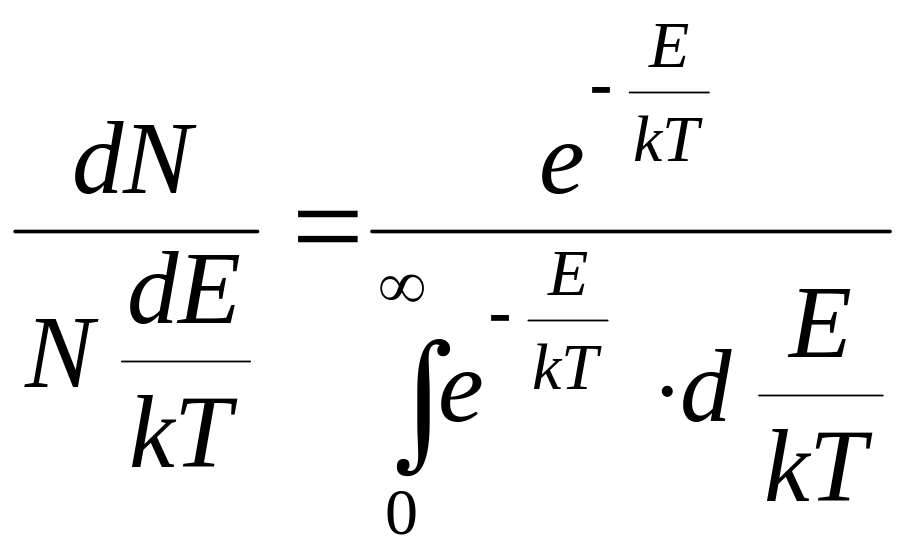. (9)
в
результате получаем:
,
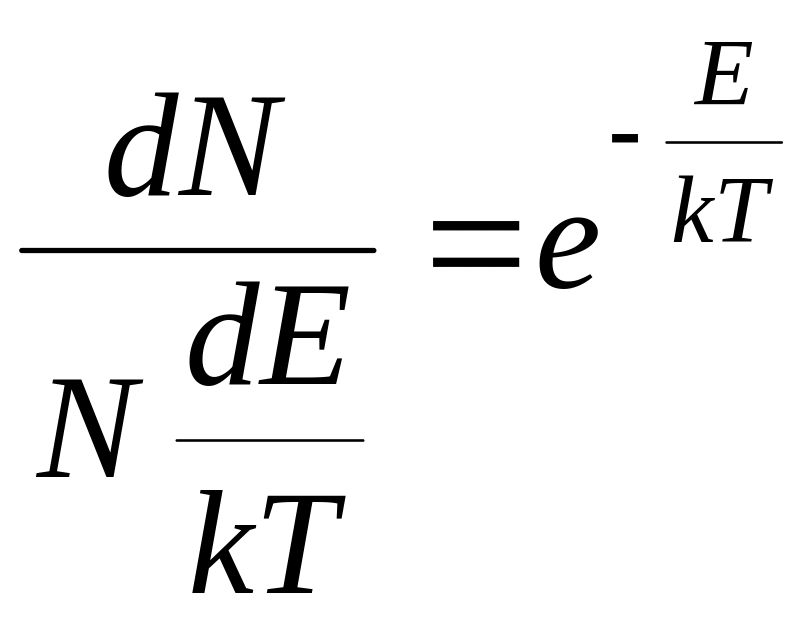(10)
или, обозначая плотность вероятности как w, получим:
.
(11)
Выражение (11) получено для постоянной температуры системы.
Энергия системы может иметь ряд слагаемых:
.
(12)
Тогда
,
или
.
(13)
Для системы, находящейся в термодинамическом равновесии, распределения частиц по энергетическим составляющим являются статистически независимыми (на основе теоремы об умножении вероятностей) и выражаются формулами Больцмана (3,6,10). Это позволяет рассматривать, к примеру, распределение частиц в электрическом поле отдельно от их распределения по кинетическим энергиям.
В классической физике энергия частиц может принимать непрерывный ряд значений. Распределение Больцмана является основой классической статистической физики, в которой считается, что изменение энергии частицы – случайное событие, попадание частицы в какой-либо интервал не зависит от заполнения интервала другими частицами.
Используем (10) для определения числа
молекул с энергией, равной или превышающей
:
,
(14)
в результате интегрирования получим
для доли частиц, энергии которых
:
.
(15)
Полученное выражение (15) можно трактовать как вероятность обнаружения частицы с энергией .
Закон Больцмана (15) применим к любым частицам, находящимся в потенциальном силовом поле и участвующим в тепловом движении. Закон Больцмана определяет условие равновесия двух противоборствующих процессов: теплового движения, стремящегося рассеять молекулы, и действия внешних сил, упорядочивающих распределение молекул.
Для частиц, находящихся в поле тяжести Земли, закон Больцмана можно записать в виде:
,
(16)
m – масса молекулы, у – высота, отсчитываемая от поверхности Земли. Аналогичное выражение можно записать для концентрации молекул:
,
(17)
и для атмосферного давления:
,
(18)
–
соответственно, концентрация молекул
и давление воздуха у поверхности Земли,
y–высота над поверхностью
Земли.
Полученные соотношения справедливы для, так называемой, «изотермической» атмосферы и для высот, значительно меньше радиуса Земли, так как при выводе соотношений мы считали g=const.
Чем больше m, тем резче изменяется концентрация данных молекул с высотой.
Однако анализ проб воздуха на разных высотах, показывает что состав атмосферы почти одинаков на разных высотах, что является признаком сильного перемешивания в атмосфере.
Формулы (16,17) показывают, что число молекул больше в тех областях силового поля, в которых потенциальная энергия молекул меньше.
С увеличением температуры число молекул, имеющих заданную потенциальную энергию, увеличивается.
Проектные задания к модулю VII:
1.Найти среднюю кинетическую энергию <Eк> поступательного движения молекул.
2.Вычислить среднюю потенциальную энергию молекулы газа в поле силы тяжести.
3.Определить долю w молекул, энергия которых заключена в пределах от 0 до 0,01kT.
4.Используя функцию распределения молекул по энергиям, определить наиболее вероятное значение кинетической энергии Ев. Соответствует ли Eв наиболее вероятной скорости?
5. Найти число молекул в воздушном столбе с основанием 1 м2 и высотой 1 км, считая температуру воздуха не зависящей от высоты и равной 00С , давление воздуха у основания равным атмосферному.
6.На какой высоте концентрация молекул уменьшается в е раз?
7.На какой высоте находится центр масс вертикального столба воздуха в изотермической атмосфере Земли температуры T?
8.Ротор центрифуги вращается с угловой
скоростью
.
Найти распределение концентрации n
частиц массой m,
находящихся в роторе центрифуги, как
функцию расстояния r
от оси вращения.
9.В сосуде находится 8 г кислорода при температуре 1600 К. Какое число молекул кислорода имеет кинетическую энергию поступательного движения, превышающую энергию 0,44 эВ?
10. Проанализировать возможные причины исчезновения атмосферы на Луне.