5. Дифференциалы функции многих переменных

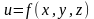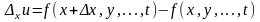Определение 5 .Частным дифференциалом функции по называется главная часть соответствующего частного приращения , линейная относительно приращения 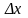(или, что то же ).

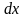Аналогично определяются частные дифференциалы функции 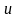по каждому из остальных ее аргументов. Частные дифференциалы функции по , по ,…, по 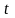обозначаются, соответственно .

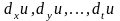Из определения частной производной следует, что

; ; …; .

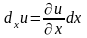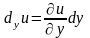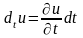Определение 6. .Полным дифференциалом функции называется главная часть ее полного приращения

,

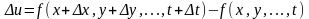линейная относительно приращения 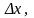,…, 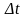(или, что то же, дифференциалов , ,…, ).

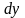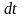Полный дифференциал 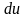функции (если он существует) равен сумме всех ее частных дифференциалов

.

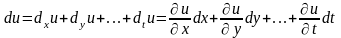Функция 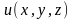называется дифференцируемой в точке (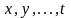 ), если в этой точке она имеет полный дифференциал.

При достаточно малых (по абсолютному значению) приращениях аргументов полное приращение функции с как угодно малой относительной погрешностью можно заменить ее полным дифференциалом

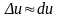
Вычисление полного дифференциала функции значительно проще, чем вычисленное ее полного приращения. Поэтому указанное приближенное равенство используется для приближенных вычислений.

Пример 7 . Найти полный дифференциал функции

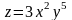
Решение. Находим частные производные данной функции:

; .

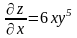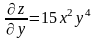Умножая частные производные на дифференциалы соответствующих аргументов, получим частные дифференциалы функции:

; .

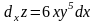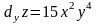Полный дифференциал функции находится как сумма ее частных дифференциалов:

.

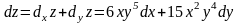Пример 8 . Вычислить значение полного дифференциала функции 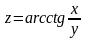при =1,01, =2,95.

Решение. Примем =1, =3, = 0,01, = -0,05.

Находим частные производные, затем частные дифференциалы и полный дифференциал:

; ; .

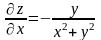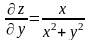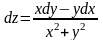Подставляя заданные значения независимых переменных, получим:

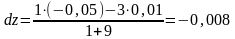
Самостоятельная работа

1. Найти полные дифференциалы функций:

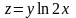
   1.1.	1.3.
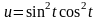
   1.2.

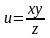
2. Вычислить значение полного дифференциала функции:

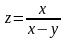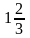при = , =1 .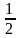

6.Дифференцирование сложной функции

Определение 7 .Переменная z называется сложной функцией от независимых переменных , если она задана через посредство промежуточных аргументов u ,v, …, w:

Z=F(u, v, …, w),

где

u=f( ); v=( ); w= ( ).

Частная производная сложной функции по одной из независимых переменных равна сумме произведений ее частных производных по промежуточным аргументам на частные производные этих аргументов по независимой переменной:

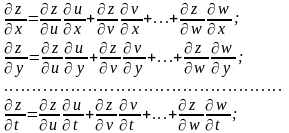(1)

Если, в частности, все аргументы 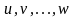будут функциями одной независимой переменной , то и будет сложной функцией только от . Производная такой сложной функции (от независимой переменной) называется полной производной и определяется формулой

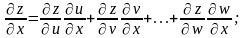(2)

Пример 9. Найти производную сложной функции:

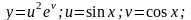
Решение: Здесь у есть сложная функция одной независимой переменной х. Пользуясь формулой (2), получим: