
- •Функция нескольких переменных и её приложения
- •Определение функции нескольких переменных
- •Самостоятельная работа
- •Частное и полное приращение функции
- •Предел функции нескольких переменных. Непрерывность
- •Самостоятельная работа
- •Частные производные функции нескольких переменных
- •Самостоятельная работа
- •Дифференциалы функции многих переменных
- •Самостоятельная работа
- •6.Дифференцирование сложной функции
- •Самостоятельная работа
- •7.Дифференцирование неявной функции
- •Самостоятельная работа
- •8. Частные производные высших порядков
- •Самостоятельная работа
- •9. Касательная плоскость и нормаль к поверхности
- •Самостоятельная работа
- •10. Экстремум функции нескольких переменных
- •Самостоятельная работа
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Решение типового варианта
- •Ответы к задаче №13
- •656038, Г. Барнаул, пр-т Ленина, 46
Вариант 22
Найти и изобразить в декартовой системе координат область определения функции:
а)
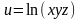 ;
;б)
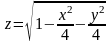 .
.Для заданной функции найти все частные производные первого порядка:
а)
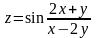 ;
;б)
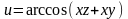 .
.Для заданной функции найти требуемые частные и смешанные производные:
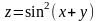 ;
;;
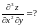
Проверить, что функция
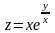 удовлетворяет заданному уравнению:
удовлетворяет заданному уравнению:
.
Найти вторые частные производные функции
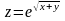 .
Убедиться в том, что
.
.
Убедиться в том, что
.Найти производные неявно заданной функции:
а)
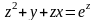 ;
и
,
;
и
,
б)
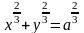 ;
.
;
.
Вычислить значение производной сложной функции
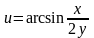 ,
где
,
,
при
.
,
где
,
,
при
.Найти градиент функции
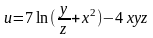 в точке А(2;1;1) и вычислить его модуль.
в точке А(2;1;1) и вычислить его модуль.Для функции вычислить градиент в точке А(1;2) и производную в направлении вектора .
Найти полный дифференциал функции.
а)
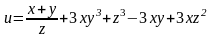 ;
;б)
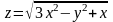 .
.С помощью полного дифференциала найти приближенное значение функции.
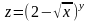 ;
;при x=0,97, y=3,02.
Найти уравнение касательной плоскости и нормали к поверхности
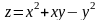 в
точке
в
точке
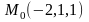 .
.Исследовать на экстремум функцию z=
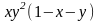 .
.
Вариант 23
Найти и изобразить в декартовой системе координат область определения функции:
а)
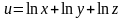 ;
;б)
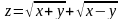 .
.Для заданной функции найти все частные производные первого порядка:
а)
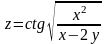 ;
;б)
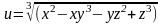 .
.Для заданной функции найти требуемые частные и смешанные производные:
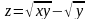 ;
;;
Проверить, что функция удовлетворяет заданному уравнению:
.
Найти вторые частные производные функции
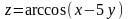 .
Убедиться в том, что
.
.
Убедиться в том, что
.Найти производные неявно заданной функции:
а)
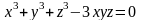 ;
и
,
;
и
,
б)
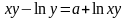 ;
.
;
.
Вычислить значение производной сложной функции
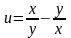 ,
где
,
где
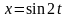 ,
,
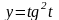 ,
при
.
,
при
.Найти градиент функции
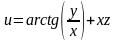 в точке А(2;2;-1) и вычислить его модуль.
в точке А(2;2;-1) и вычислить его модуль.Для функции
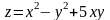 вычислить градиент в точке А(1;2) и
производную в направлении вектора
вычислить градиент в точке А(1;2) и
производную в направлении вектора
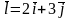 .
.Найти полный дифференциал функции.
а)
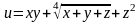 ;
;б)
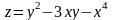 .
.С помощью полного дифференциала найти приближенное значение функции.
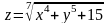 ;
;при x=3,05, y=1,98.
Найти уравнение касательной плоскости и нормали к поверхности
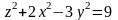 в
точке
в
точке
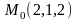 .
.Исследовать на экстремум функцию z=
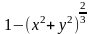 .
.
Вариант 24
Найти и изобразить в декартовой системе координат область определения функции:
а)
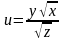 ;
;б)
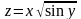 .
.Для заданной функции найти все частные производные первого порядка:
а)
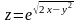 ;
;б)
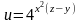 .
.Для заданной функции найти требуемые частные и смешанные производные:
;
;
Проверить, что функция
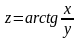 удовлетворяет заданному уравнению:
удовлетворяет заданному уравнению:
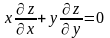 .
.
Найти вторые частные производные функции
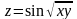 .
Убедиться в том, что
.
.
Убедиться в том, что
.Найти производные неявно заданной функции:
а)
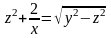 ;
и
,
;
и
,
б)
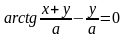 ;
.
;
.
Вычислить значение производной сложной функции
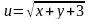 ,
где
,
,
при
1.
,
где
,
,
при
1.Найти градиент функции
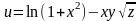 в точке А(1;-2;4) и вычислить его модуль.
в точке А(1;-2;4) и вычислить его модуль.Для функции
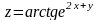 вычислить градиент в точке А(0;0) и
производную в направлении вектора
вычислить градиент в точке А(0;0) и
производную в направлении вектора
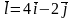 .
.Найти полный дифференциал функции.
а)
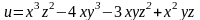 ;
;б)
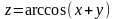 .
.С помощью полного дифференциала найти приближенное значение функции.
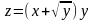 ;
;при x=0,97, y=4,01.
Найти уравнение касательной плоскости и нормали к поверхности
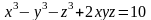 в точке
в точке
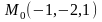 .
.Исследовать на экстремум функцию z=
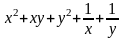 .
.
