
- •Функция нескольких переменных и её приложения
- •Определение функции нескольких переменных
- •Самостоятельная работа
- •Частное и полное приращение функции
- •Предел функции нескольких переменных. Непрерывность
- •Самостоятельная работа
- •Частные производные функции нескольких переменных
- •Самостоятельная работа
- •Дифференциалы функции многих переменных
- •Самостоятельная работа
- •6.Дифференцирование сложной функции
- •Самостоятельная работа
- •7.Дифференцирование неявной функции
- •Самостоятельная работа
- •8. Частные производные высших порядков
- •Самостоятельная работа
- •9. Касательная плоскость и нормаль к поверхности
- •Самостоятельная работа
- •10. Экстремум функции нескольких переменных
- •Самостоятельная работа
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Решение типового варианта
- •Ответы к задаче №13
- •656038, Г. Барнаул, пр-т Ленина, 46
Министерство образования и науки Российской Федерации
Алтайский Государственный Технический Университет
им. И.И.Ползунова
Е.В Мартынова, И.П. Мурзина
Функция нескольких переменных и её приложения
Учебно-методические указания и варианты индивидуальных заданий для студентов технических и экономических специальностей
Барнаул 2007
УДК 517.17
Мартынова Е.В., Мурзина И.П.: Функция нескольких переменных и её приложения. Методические указания и варианты заданий для организации самостоятельной работы студентов технических и экономических специальностей по курсу математики./ Е.В Мартынова, И.П. Мурзина; Алт. гос. техн. ун-т им. И.И.Ползунова. – Барнаул: Изд-во АлтГТУ, 2007. – 60с.
Пособие содержит теоретические сведения и наборы задач для индивидуальных заданий по теме: Функция нескольких переменных и её приложения.
Рассмотрено и одобрено на заседании кафедры высшей математики и математического моделирования.
Протокол №10 от 6 июня 2007г.
Рецензент: И.В.Лощина, доцент кафедры ВМ и ММ Алт ГТУ
Методическая разработка по курсу ’’Функция нескольких переменных и её приложения’’ содержит теоретические сведения и указания, а также 30 различных вариантов по 13 заданий, которые составлены в соответствии с рекомендациями, изложенными в курсе «Высшей математике» для инженерно-технических специальностей. Приводится пример решения типового варианта. Для вторичного закрепления материала в конце каждого параграфа даны примеры заданий по рассмотренной теме.
Цель пособия – помочь изучающим в усвоении необходимых теоретических знаний и в приобретении и закреплении навыков при решении задач по теме «Функция нескольких переменных и её приложения».
Одним из важных факторов усвоения курса высшей математики является активная самостоятельная работа студента. Система индивидуальных заданий для самостоятельной работы способствует более глубокому изучению материала. Варианты заданий предназначены для организации индивидуальной самостоятельной работы студентов всех специальностей АлтГТУ, что поможет активизировать познавательную деятельность студентов, выработать у них навыки самостоятельного решения достаточно сложных задач, а также могут быть использованы при проведении практических занятий.
Решение задач, включенных в варианты, предполагает изучение студентами следующих теоретических вопросов:
Определение функции нескольких переменных. Частное и полное приращение функции. Непрерывность функции нескольких переменных.
Частные производные функции нескольких переменных.
Дифференцирование сложных и неявных функций нескольких переменных.
Полный дифференциал функции нескольких переменных и его применение к приближенным вычислениям.
Касательная плоскость и нормаль к поверхности.
Экстремум функции двух переменных.
Производная по направлению, градиент.
Определение функции нескольких переменных
Пусть каждой
упорядоченной паре чисел
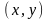 из некоторой области D
соответствует определенное число
из некоторой области D
соответствует определенное число
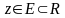 .
Тогда
.
Тогда
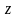 называется функцией двух переменных
называется функцией двух переменных
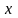 и
и
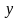 ,
,
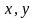 – независимыми переменными или
аргументами, D –
областью определения или существования
функции, а множество Е всех значений
функции – областью ее значений.
Символически функция двух переменных
записывается в виде равенства
– независимыми переменными или
аргументами, D –
областью определения или существования
функции, а множество Е всех значений
функции – областью ее значений.
Символически функция двух переменных
записывается в виде равенства
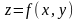 ,
в котором
,
в котором
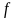 обозначает закон соответствия. Этот
закон может быть задан аналитически
(формулой), с помощью таблицы или графика.
Всякое уравнение
определяет
в пространстве, в котором введена
декартова система координат
обозначает закон соответствия. Этот
закон может быть задан аналитически
(формулой), с помощью таблицы или графика.
Всякое уравнение
определяет
в пространстве, в котором введена
декартова система координат
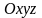 ,
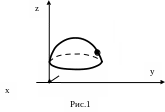
некоторую поверхность, образованную
множеством точек
,
некоторую поверхность, образованную
множеством точек
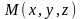 пространства, координаты которых
удовлетворяют уравнению
(рис.
1).
пространства, координаты которых
удовлетворяют уравнению
(рис.
1).
Геометрически
область определения функции D
обычно представляет собой некоторую
часть плоскости
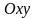 ,
ограниченную линиями, которые могут
принадлежать или не принадлежать этой
области. В первом случае область D
называется замкнутой и обозначается
,
ограниченную линиями, которые могут
принадлежать или не принадлежать этой
области. В первом случае область D
называется замкнутой и обозначается
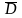 ,
во втором – открытой.
,
во втором – открытой.
Пример 1. Вычислить частное значение функции:
1.1.
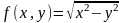 при
=5,
=-3;
при
=5,
=-3;
1.2.
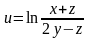 в точке А(6;2;-1).
в точке А(6;2;-1).
Решение.
1.1.
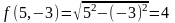
1.2.
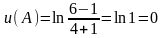
Пример 2.
Построить область определения D
переменных
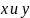 ,
заданную следующими неравенствами:
,
заданную следующими неравенствами:
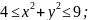
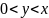 .
.
Решение.
Здесь область
 есть круговое кольцо, ограниченное
окружностями
есть круговое кольцо, ограниченное
окружностями
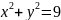 и
и
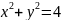 с общим центром вначале координат и
радиусами
с общим центром вначале координат и
радиусами
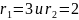 .
Точки, лежащие на окружностях (граница
области), входят в область. Такая область,
в которую входят и её границы, называется
замкнутой (рис.2).
.
Точки, лежащие на окружностях (граница
области), входят в область. Такая область,
в которую входят и её границы, называется
замкнутой (рис.2).
2.2. Здесь область (открытая) ограниченна биссектрисой первого координатного угла и осью абсцисс (рис.3).◄
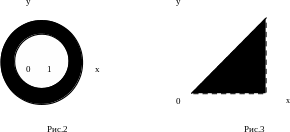
Пример 3. Найти область определения функции:
3.1.
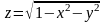
3.2.
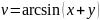 .
.
Решение.
Для того, чтобы имело действительное значение, нужно, чтобы под корнем стояло неотрицательное число, т.е. и должны удовлетворять неравенству
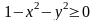 ,
или
,
или
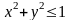 .
Все точки М
,
координаты которых удовлетворяют
указанному неравенству, лежат в круге
радиуса 1 с центром в начале координат
и на границе этого круга. Графическим
изображением функции является полусфера,
расположенная над плоскостью
.
Все точки М
,
координаты которых удовлетворяют
указанному неравенству, лежат в круге
радиуса 1 с центром в начале координат
и на границе этого круга. Графическим
изображением функции является полусфера,
расположенная над плоскостью
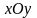
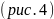 .
.Областью определения функции
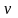 есть совокупность систем значений
и
удовлетворяющих неравенствам
есть совокупность систем значений
и
удовлетворяющих неравенствам
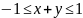 .
На плоскости
.
На плоскости
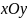 эта область представляет полосу,
ограниченную параллельными прямыми
эта область представляет полосу,
ограниченную параллельными прямыми
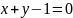 и
(рис.5).◄
и
(рис.5).◄

Определение функции двух переменных легко обобщить на случай трех и более переменных.
Определение 1. Если каждой рассматриваемой совокупности значений переменных х, у, z, … u, t соответствует определенное значение переменной w, то будем называть w функцией независимых переменных х, у, z, … u, t и писать w=F(х, у, z, … u, t) или w=f(х, у, z, … u, t) и т.д.
