2.5. Описание состояния системы.

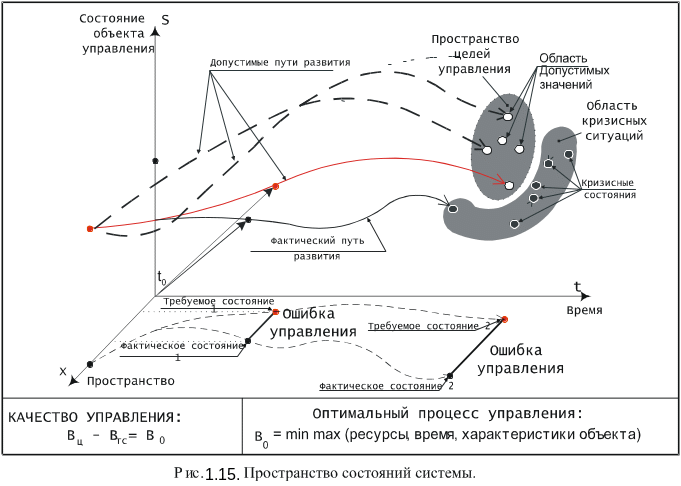
Состояние любой системы с заданной точностью можно охарактеризовать совокупностью значений величин т, определяющих ее поведение, т.е. вектором состояния систем (см. Рис. 1.15).

Эти величины позволяют сравнивать состояния отдельных систем и судить об их различии, сравнивать состояния одной и той же системы в произвольные моменты времени для выяснения ее движения.

Из всех существующих форм описания состояния системы наибольший интерес представляет способ, основанный на понятии пространства состояний системы. Пространством состояний системы называется многомерное пространство, в котором каждое состояние системы изображается точкой, называемой изображающей точкой (она «изображает данное состояние системы), координаты которой — переменные состояния системы m₁, т₂, ..., m_n.

В реальных системах не все координаты могут изменяться в неограниченных пределах. Большая часть координат принимает значения, лежащие в ограниченном интервале m_c, т_i т_s,

где, c, s — границы интервала возможных значений координаты т_i.

Область пространства состояний, в которой находится изображающая точка, называется областью допустимых состояний.

Пример.

1. Допустимые состояния автомобиля определяются по нескольким параметрам: по величине крена, по углу разворота, по скорости, по давлению масла в двигателе, по температуре охлаждающей жидкости, давлению воздуха в колесах и т.д.

2. Допустимое физиологическое состояние организма человека определяется по: окружающей температуре, атмосферному давлению, радиационному фону, информационному воздействию и т.д.

Говоря о пространстве состояний, имеют в виду лишь его допустимую область. Однако даже в ней не всегда любая точка изображает возможное состояние системы. Таким свойством обладает лишь непрерывное пространства состояний, соответствующее системе, координаты которой принимают любые значения (в допустимых пределах). Существуют системы (дискретные), в которых координаты принимают конечное число фиксированных значений. Пространство состояний этих систем также дискретно.

Пример.

1. Вождение автомобиля по трассе – непрерывный процесс, но переключение передач при определенной скорости – дискретный процесс. Поток автомобилей на городских улицах – непрерывный процесс, а их проезд через регулируемые светофором перекрестки – дискретный процесс.

2. Процесс обучения – непрерывный процесс, а контроль уровня знаний посредством выставляемых оценок – дискретный процесс.

Таким образом, управление представляет собой процесс динамического имитационного моделирования субъектом управления перевода системы из одного устойчивого по допустимым параметрам состояния в другое с учетом факторов влияния на процессы деятельности, структуры внешних и внутренних связей и способности обеспечения самого управления.

2.6. Взаимовложенность систем и процессов управления.

2.6.1. Понятие взаимовложенности систем

и процессов управления.

Любая система может быть разделена на подсистемы. Объекты, принадлежащие одной системе, с успехом могут рассматриваться как части окружающей среды или элементы другой подсистемы. (Рис 1.16.) Анализ подсистемы требует изучения новой совокупности отношений (рис. 1.17). Иногда отмечают свойства иерархической упорядоченности систем, а по сути дела, имеется возможность разделения систем на подсистемы. Эту мысль можно выразить иначе, сказав, что элементы системы сами могут быть системами низших порядков. Понятие подсистемы используется для анализа сложноорганизованных, саморазвивающихся систем, в которых между элементами и системой, как целым, могут быть выделены промежуточные «ступени», более сложные в некотором смысле, чем элементы и менее сложные, чем системы.

Примеры.

1. Образное представление взаимовложенности систем дает русская матрешка. Количество матрешек может быть задано любое, каждая бóльшая может быть похожа, либо отличаться от ее составляющих.

2. Кровеносная система может быть рассмотрена как подсистема организма человека. Но органы ее составляющие также могут рассматриваться как системы: сердце, вены, артерии, капилляры и т.д., Системы более низкого уровня – ткани, клетки.

3. Карманные деньги каждого человека – это подсистема бюджета семьи. Бюджет семьи – это подсистема более сложной кредитно-финансовой системы города, субъекта РФ, страны. В свою очередь финансовая система РФ в настоящее время является мировой кредитно-финансовой системой.

4. Идея исследования подсистем и их поведения широко применяется в математике, особенно в теории множеств. Так изучение групп (совокупностей математических объектов, имеющих некоторые алгебраические свойства) включает исследование свойств подгрупп; более того, подгруппы не обязательно «ведут» себя во всех отношениях так же, как содержащие их группы (поведение здесь имеет алгебраический смысл).

5. Процессы управления личной жизнью взаимовложены в процессы управления в семье, в трудовом или учебном коллективе; те в свою очередь взаимовложены в процессы управления в государстве, цивилизации, которые являются составляющими глобального исторического процесса, а процессы глобального исторического процесса являются составляющими глобального эволюционного процесса.

Поскольку системность представляет собой неотъемлемое свойство Мирозданья, внутренне ему присущее, постольку окружающая систему среда может быть определена, как система более высокого уровня, объемлющая ограниченную систему, то система образует единство со средой, в силу чего правомерно говорить о взаимной вложенности систем и протекающих в них процессов управления.

Взаимовложенность систем характеризует возможность влияния на них других систем, т.е. говорят об их открытости. Исследование открытых систем, к которым относятся социальные системы, чрезвычайно затруднено их вы­сокой размерностью, а, следовательно, сложностью систем и подсистем. Но по аналогии взаимовложенности систем имеет место взаимовложенность процессов управления (рис. 1.18, 1.19).