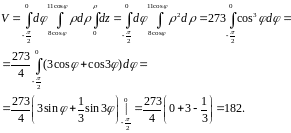- •Лекция 4. Двойные и тройные интегралы, их определения, свойства и вычисление путем сведения к повторным интегралам. Вычисление площадей плоских фигур и объёмов тел
- •1. Двойной интеграл, его свойства и вычисление
- •2. Тройной интеграл, его свойства и вычисление
- •3. Приложения кратных интегралов
- •1 . Криволинейные координаты на плоскости
- •2. Двойной интеграл в полярных координатах
- •3. Криволинейные координаты в пространстве. Тройной интеграл в цилиндрических и сферических координатах
- •4. Площадь поверхности
2. Двойной интеграл в полярных координатах
Рассмотрим
функции
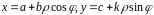
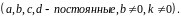 Эти функции будут взамно одноз-
Эти функции будут взамно одноз-
начно
отображать плоскость переменных
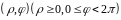 на плоскость переменных
на плоскость переменных
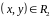 ,
если условиться, что точка
,
если условиться, что точка
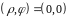 переходит только в точку
переходит только в точку
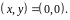 Криволинейные координаты
Криволинейные координаты
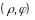 называют в этом случае обобщенными
полярными координатами,
а в случае
называют в этом случае обобщенными
полярными координатами,
а в случае
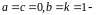 просто полярными
координа-тами в плоскости
Вычислим якобиан перехода для таких
координат. Имеем
просто полярными
координа-тами в плоскости
Вычислим якобиан перехода для таких
координат. Имеем

Из теоремы 1 вытекает, что двойной интеграл в обобщенных полярных координатах будет таким:
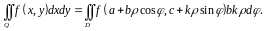
При
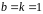 получаем формулу
получаем формулу
для
двойного интеграла в полярных координатах.
Здесь и выше
 область,
которая при отображении
переходит в область
область,
которая при отображении
переходит в область
Пример
1 ((Кузнецов
Л.А. Типовые расчеты).
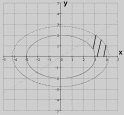
Пластинка
задана неравенствами
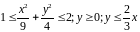 ,
,
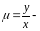 поверхностная
плотность. Найти массу пластинки.
поверхностная
плотность. Найти массу пластинки.
 Решение.
Введем
обобщенные полярные координаты
Решение.
Введем
обобщенные полярные координаты
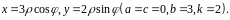
При
этом эллипсы
 перейдут в прямые
перейдут в прямые
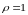 и
и
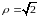 соответственно, а прямая
соответственно, а прямая
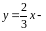 в луч
в луч
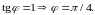 Якобиан перехода будет таким:
Якобиан перехода будет таким:
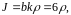 поэтому
поэтому
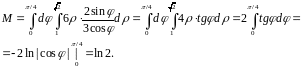
3. Криволинейные координаты в пространстве. Тройной интеграл в цилиндрических и сферических координатах
Криволинейные
координаты в пространстве вводятся
аналогично. Если
 область переменных
область переменных
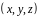 ,
заданных в прямоугольных декартовых
координатах, то упорядочная тройка
чисел
,
заданных в прямоугольных декартовых
координатах, то упорядочная тройка
чисел
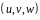 ,
связанная с предыдущей тройкой
равенствами
,
связанная с предыдущей тройкой
равенствами
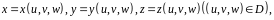
осуществляющими
взаимно однозначное отображение области
на область
называется криволинейными координатами
точки
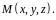 При этом поверхности
При этом поверхности
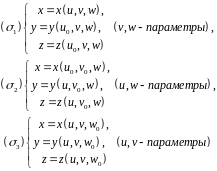
называются
координатными поверхностями точки
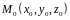 (пересечением именно этих поверхностей
является точка
(пересечением именно этих поверхностей
является точка
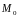 ).
Определитель
).
Определитель
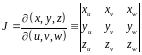
называется
якобианом
отображения (4) или якобианом перехода
от декартовых координат к криволинейным.
Его геометрический смысл состоит в
следующем:
 есть коэффициент искажения объёма
малого параллелепипеда с вершиной в
точке
есть коэффициент искажения объёма
малого параллелепипеда с вершиной в
точке
 и рёбрами
и рёбрами
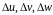 при отображении (4), т.е.
при отображении (4), т.е.
 где
где
 объём
образа указанного параллелепипеда при
отображении (4). Используя этот факт,
нетрудно доказать следующее утверждение.
объём
образа указанного параллелепипеда при
отображении (4). Используя этот факт,
нетрудно доказать следующее утверждение.
Теорема 2. Имеет место равенство
 если
выполняются следующие условия:
если
выполняются следующие условия:
1)
функция
непрерывна в замкнутой ограниченной
области

2)
функции
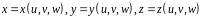 непрерывно
дифференцируемы в области
и взаимно однозначно отображают область
на область
непрерывно
дифференцируемы в области
и взаимно однозначно отображают область
на область
3)
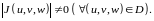
Цилиндрическими
координатами
называются координаты
 точки
точки
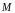 ,
связанные с декартовыми координатами
этой точки равенствами (см. Р.18)
,
связанные с декартовыми координатами
этой точки равенствами (см. Р.18)
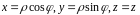
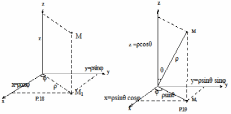
 Нетрудно
подсчитать, что якобиан перехода от
декартовых координат к цилиндрическим
будет равен
Нетрудно
подсчитать, что якобиан перехода от
декартовых координат к цилиндрическим
будет равен
 Действительно, имеем
Действительно, имеем
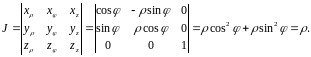
Следовательно, тройной интеграл в цилиндрических координатах запишется так (см. (5)):


Здесь
область, которая при отображении
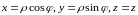 переходит в область
переходит в область
Сферическими
координатами
называются координаты
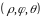 точки
,
связанные с декартовыми координатами
этой точки равенствами (см. Р.19)
точки
,
связанные с декартовыми координатами
этой точки равенствами (см. Р.19)
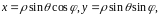
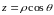
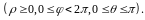
Нетрудно
показать, что якобиан перехода от
декартовых координат к сферическим
равен
 Используя теорему 2, запишем тройной
Используя теорему 2, запишем тройной
интеграл в сферических координатах в виде
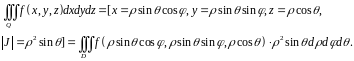
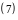
Здесь
область, которая при отображении
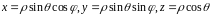 переходит в область
переходит в область
Пример 2 (Кузнецов Л.А. Типовые расчеты). Найти объем тела, заданного ограничиваю-
щими его поверхностями:
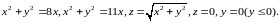
Решение.
Объём
тела будем вычислять с помощью тройного
интеграла
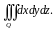 Введём цилиндрические координаты:
Введём цилиндрические координаты: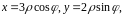
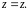 Тогда область
перейдёт в область
Тогда область
перейдёт в область
 граница которой будет задаваться
уравнениями
граница которой будет задаваться
уравнениями
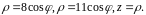 Граница проекции тела
на плоскость
Граница проекции тела
на плоскость
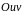 будет такой
будет такой
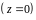 :
:
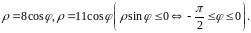
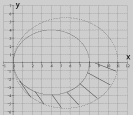 Луч
с произвольным углом
Луч
с произвольным углом
 выходящий из начала
выходящий из начала
 пересекает эту границу сначала в точке
пересекает эту границу сначала в точке
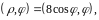 а затем – в точке
а затем – в точке
 Значит, нижний и верхний пределы по
Значит, нижний и верхний пределы по
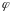 в повторном интеграле будут соответственно
в повторном интеграле будут соответственно
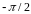 и
и
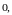 а пределы по
а пределы по
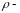 соответственно
соответственно
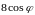 и
и
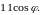 Взяв произвольно точку
Взяв произвольно точку
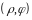 в проекции
на плоскость
в проекции
на плоскость
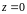 ,
выпустим из неё луч в направлении оси
Он сначала пересечёт нижнюю границу
области
в точке
,
выпустим из неё луч в направлении оси
Он сначала пересечёт нижнюю границу
области
в точке
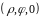 ,
а затем верхнюю границу области
в точке
,
а затем верхнюю границу области
в точке
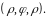 Значит,
пределы по
в повторном интеграле будут соответственно
и
Значит,
пределы по
в повторном интеграле будут соответственно
и
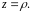 В результате будем иметь
В результате будем иметь