3. Решение:

Приравнивая данные функции L_s= L_d, получим 10 + 1/2w= 100-w, откуда w = 60 ден. ед. Объем предлагаемого труда равен L_d = 100-w = 100-60=40 ед.

Профсоюз будет действовать на рынке труда так же, как моно­полист на рынке блага. Условием максимизации его прибыли является равенство MR_u = МС_u, где МР_u - предельный доход профсоюза от найма предпринимателями дополнительного члена профсоюза, а МС_u - предельные издержки, которые описываются функцией отраслевого предложения труда. МR_u = (L_d*w)'=(L*(100 –L))`= 100 – 2L. Функцию предложения труда можно представить виде: w = 2L-20. 100-2L = 2L -20. отсюда L= 30. Если профсоюз ограничит величину предложения труда 30 ед., то ставка заработной платы в соответствии с функцией спроса на труд вырастет до w_m = 100 - 30=70 ден. ед.

Ответ: w_c= 60 ден. ед., L_С = 40; w_т = 70 ден. ед.

4. Решение:

Предположим, что инвестиции осуществляются в начале каждого года, а прибыли рассчитывается на конец года. В этих условиях стои­мость инвестиций, приведенная к текущему моменту, составляет:

РV₁ =

= 2272,73. Приведенная к текущему моменту

величина выручки составит: РV_R =

+

+ ...+

. Перед нами геометрическая прогрессия, первый член которой a₁=

, а знаменатель q=

. По формуле суммы n членов геометрической прогрессии имеем:

S_n=

имеем:

PV_R=

=

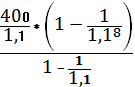
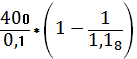
=400*(1-

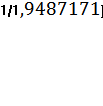
=1947,37

NPV=PV_R- PV₁=1947,37-2272,73=-325,36 тыс.

Ответ: NPV<0, инвестиции осуществлять не стоит.

5. Решение:

Предположим, что зарплату за весь год можно получить в начале года, а оплата обучения также осуществляется в начале года.

Теперь приведем величину инвестиций к концу второго года. Ее моменту, когда менеджер, окончив курсы, сможет подучить первую зарплату па повышенной ставке): РV₁= 100* 1,44 +100 * 1,2 = 264 тыс. Это значит, что если средства (100 тыс. в текущем году и 100 тыс. в следующем), потраченные на оплату курсов, положить в какой под 20% годовых, то к концу второго года они вырастут и составят 264тыс. Рассчитаем величину дополнительного дохода, который менеджер сможет получать, окончив курсы. К началу третьего года он будет пред­ставлять собой бесконечный поток дохода, размер которого составляет разницу между его новой зарплатой и старой: РV_R = (5-2) *

=180 тыс.

Отсюда NPV=PV_R-PV₁=180-264=84 тыс., т.е. смысла учмться нет.

Ответ: МРV < 0, инвестиции осуществлять не стоит.

6. L=0,1 млн чел. -ч.

7. 100 человек.

8. 1. L_d=

2. 20 тыс.

3. -5 тыс.

4. 15 тыс.

5. L_s=0,22w+15,55.

9. 1. L=20=1/6w.

2. L=10.

3.

L=-5.

4. 10.

10. 1. L=5.

2. L=1; П=1.

3. нет ( при L=6, П=-24).

11. 1. L=1.

2.

L=-0,4.

3.

П=-3,2.

12. 1.L = 667-3.33w.

2. L = 500.

3.L = 470;w = 49,4

13. w_с = 40ден.ед.;L_с= 20;w_m = 42,5ден.ед.,т.е увеличится на 2,5.

14. w_с=15ден ед.; L_с =70; w_m = 27 ден. ед., т. е. увеличится на 12.

15. L_m = 30;160≤ w_m ≤280 ден. ед.

16.NPV = +200 тыс. долл.; инвестиции осуществлять стоит.

17.NPV > 0; инвестиции осуществлять стоит.

18.4489долл.

19.2182долл.

20.100тыс. долл.

21. 22898,5

22.NPV=-0,14млн руб. Не стоит.

23. NPV = -0,12 млн руб. Не стоит.

24.1,74%.

25 . R = 6 тыс. руб.; Р = 50 тыс. руб.