Геометрический расчет зубчатых колёс редуктора

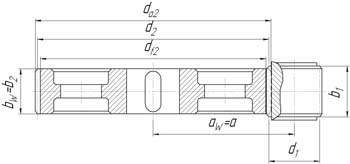
2. Основные геометрические параметры цилиндрической передачи

4.1. Делительные диаметры колес:

d₁ = = = 81,4545 мм,

d₂ = = = 366,5455 (мм).

Проверка межосевое расстояние по делительным диаметрам колес:

0,5 ∙ (81,4545 + 366,5455) = 224 мм.

4.2.Диаметры вершины зубьев:

=81,4545 + 2 · 5,0 = 91,4545 мм;

=366,5455 + 2 · 5,0 = 376,5455 мм.

4.3. Диаметры впадин зубьев:

= 81,4545 – 2,5 · 5,0 = 68,9545 мм;

= 366,5455 – 2,5 · 5,0 = 354,0455 мм.

4.4. Окружная скорость передачи.

; = 12,10 м/с.

При такой скорости, для косозубых колес, принята 8-я степень точности.

4.5.Силы, действующие в зацеплении:

Окружная сила

Ft₁ = Ft₂ = Ft = = = 2903 ≈ 2910 Н.

Радиальная сила

Fr₁ = Fr₂ = = = 1078 ≈ 1080 Н, где tgα, α = α_W = 20⁰ , т.е tgα = 0,364

Осевая сила

Fа₁ = Fа₂ = Ft · tgβ = 2910 · 0,1916 = 557 ≈ 560 Н.

Проверка на контактную выносливость и изгибную прочность зубьев

5.1.Проверочный расчёт передачи на контактную выносливость.

Расчетного напряжения, из условия обеспечения контактной выносливости зубьев:

,где

– коэффициент нагрузки, при проверке на контактную выносливость:

, где

1,12 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями (п. 4.3. [8]);

1,26 – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, связанную с деформацией валов и самих зубьев колес (по Табл. 4.3. [8]);

1,08 – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении (по Табл. 4.6. [8]);

1,12 · 1,26 · 1,08 = 1,52.

= 372 МПа ≤ 355 МПа

Перегрузка составляет:

; = -5 %.

Фактические контактные напряжения могут превышать допускаемые не более чем на 5 %. Недогрузка по контактным напряжениям не может превышать 1015 %.

5.2. Проверочный расчёт передачи на изгибную выносливость.

,где

– коэффициент нагрузки при проверке на изгибную выносливость.

, где

0,91 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями, зависящий от степени точности изготовления (п. 4.3. [8]);

1,08 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (по Табл. 4.4. [8]);

1,29 – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении (по Табл. 4.7. [8]);

0,91 · 1,08 · 1,29 = 1,27.

Y_β – коэффициент наклона линии зуба,

Y_ =1 – ; Y_ = 1 – = 0,92

коэффициент формы зуба, определяется в зависимости от эквивалентных чисел

зубьев : ; = = 17;

= = 76.

По таблице 4.12 [8] 4,28, 3,6.

= 34 МПа ≤ 204 МПа;

= 41 МПа ≤ 227 МПа.

.

1. Основные параметры проектируемой зубчатой передачи цилиндрического редуктора.

Параметры		Значения
Мощность двигателя Рном,(кВт)		45
Именование двигателя		4А200L2У3
Вращающий момент на ведущем валу Т1, Н·м		121
Вращающий момент на ведомом валу Т2, Н·м		532
Частота вращения вала ведущего п1, мин-1		2940
Частота вращения вала ведомого п2, мин-1		630
Угловая скорость вала ведущего ω1, с-1		308
Угловая скорость вала ведомого ω2, с-1		66
Передаточное число и		4,50
Межосевое расстояние а, мм		224
Модуль зацепления mn, мм		5,0
Передача (форма зуба)		косозубая
Угол наклона линии зуба β		10º 51´
Окружная скорость в зацеплении		12,10
Степень точности передачи		8
Силы, действующие в зацеплении,
окружная Ft, Н		2910
радиальная Fr, Н		1080
осевая Fa,Н		560
Параметры	шестерня [1]	колесо [2]
Материал	45	45
Твёрдость, HB	220	190
Термическая обработка	нормализация	нормализация
Число зубьев	16	72
Диаметр, мм
делительный d	81,4545	366,5455
вершин зубьев da	91,4545	376,5455
впадин зубьев df	68,9545	354,0455
Ширина венца b, мм	75	71
Напряжения, МПа
Допускаемое [σн]	355
Расчетное σн	372
Допускаемое [σF]	227	204
Расчетное σF	41	34