
Инспекция Тульской области по надзору и контролю в сфере образования
Аккредитационные педагогические измерительные материалы
для проведения педагогических измерений качества подготовки обучающихся и выпускников образовательных учреждений, расположенных на территории Тульской области,
в ходе государственной аккредитации образовательных учреждений
государственное образовательное учреждение среднего профессионального образования Тульской области «Тульский государственный коммунально-строительный техникум»
по математике
Курс 2
Тула 2012
Пояснительная записка
к аккредитационным педагогическим измерительным материалам
для проведения педагогических измерений качества подготовки обучающихся и выпускников образовательных учреждений, расположенных на территории Тульской области,
в ходе государственной аккредитации образовательных учреждений
государственное образовательное учреждение среднего профессионального образования
Тульской области «Тульский государственный коммунально-строительный техникум»
по математике
Аккредитационные педагогические измерительные материалы подготовлены для выпускников 2 курса с целью оценки качества подготовки и определения уровня знаний и умений, их соответствия требованиям действующего Государственного образовательного стандарта по математике.
Педагогический тест содержит 18 тестовых заданий одинаковой трудности.
Первая часть педагогического теста включает 15 заданий. Каждое тестовое задание содержит 4 варианта ответов, один из которых является правильным.
Вторая часть педагогического теста состоит из 3 заданий. Ответы к этим заданиям должны быть сформулированы самостоятельно. Если ответ на задание — это слово (слова) или словосочетание, то нужно написать их в той форме (падеж, род, число и т.п.), в которой они стоят в задании. Если в ответе требуется указать несколько слов либо цифр, писать их следует через запятую.
При выполнении педагогического теста могут использоваться вспомогательные средства (микрокалькуляторы).
Для каждого варианта педагогического теста подготовлены эталоны ответов для проверки результатов педагогических измерений.
Расчетное время выполнения педагогического теста без учета времени предварительного инструктажа 45 минут.
ОУ _________________________________________________________________________________
Курс _____ Группа ______________________ № (по списку)_________________________________
Математика Вариант 1
1. Что называется числовой последовательностью?
ряд чисел, заданных формулой;
ряд векторов;
ряд производных;
ряд интегралов.
2. Последовательность задана формулой общего элемента хn= n2. Определить первые три члена этой последовательности.
0; 1; 2;
1; 4; 9;
2; 6; 8;
1; 1; 1.
3. Чему равно
значение предела
![]() ?
?
0;
4;
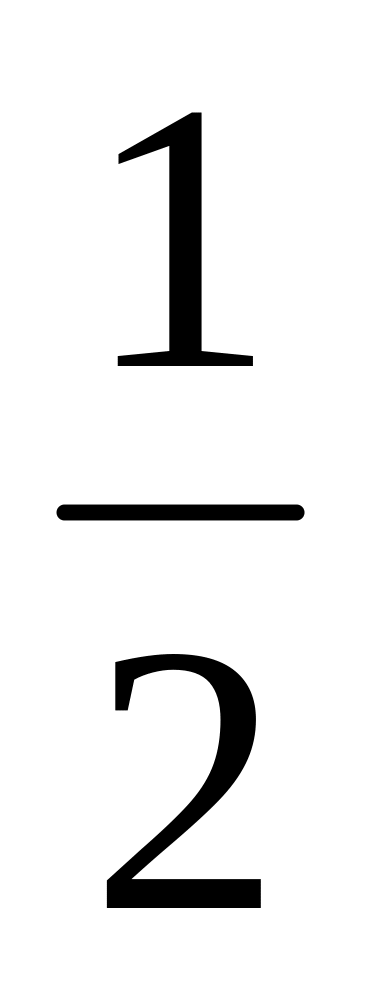 ;
;∞.
4. Найти
значение прдела
![]() .
.
-2;
3;
∞;
0.
5. Чему равно
значение предела
![]() ?
?
е2;
∞;
0;
е–2.
6. Найти значение
производной функции
![]() в точке
в точке
![]() .
.
2e;
e;
1 + e;
2 + e.
7. Найти производную функции у = (3х – 2)12.
у' = 12(3х – 2)11 ;
у' = 36х(3х – 2) 11;
у' = 36(3х – 2) 11;
у' = 12х(3х – 2) 11.
8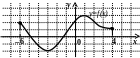 .
Функция у
= f(x)
задана на промежутке [– 6; 4]. Какому
промежутку, принадлежат все точки
экстремума?
.
Функция у
= f(x)
задана на промежутке [– 6; 4]. Какому
промежутку, принадлежат все точки
экстремума?
[– 6; 0];
[0; 4];
[– 2; 3];
[– 3;1].
9.
Вычислить неопределенный интеграл
![]()
ln|cosx| + C;
ln|sinx| + C;
tgx +C;
ctgx + C.
10. Какое из диффреренциальных уравнений первого порядка есть уравнение с разделенными переменными?
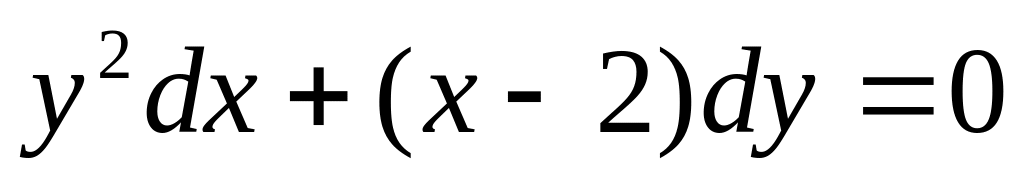 ;
;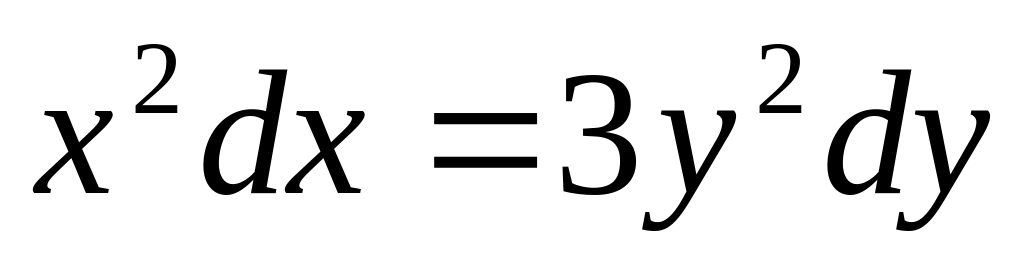 ;
;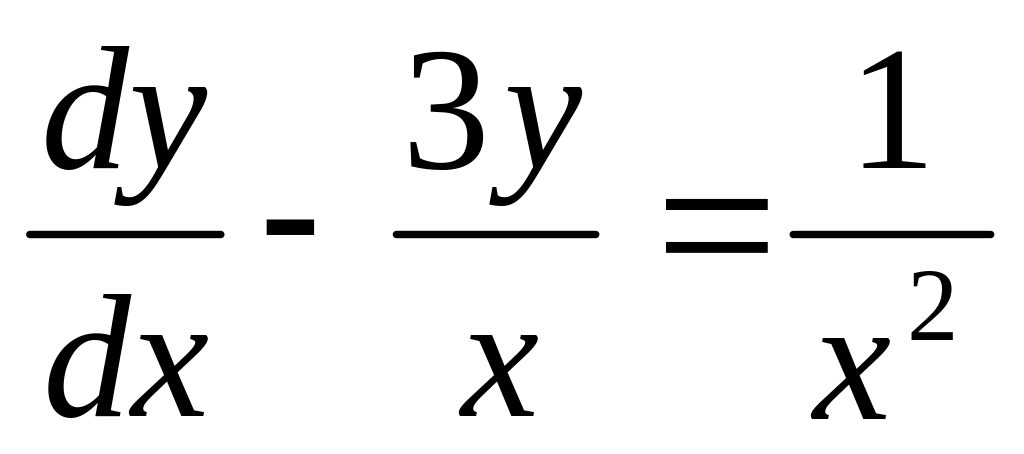 ;
;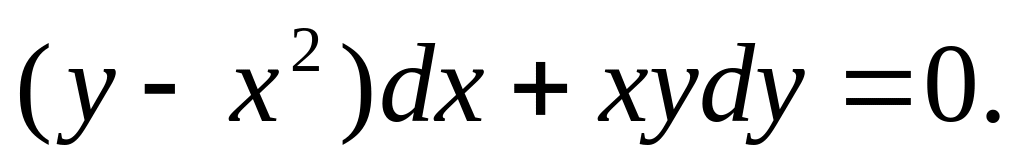
11. Какое решение имеет дифференциальное уравнение первого порядка с разделяющимися переменными dy = x2dx?
y =
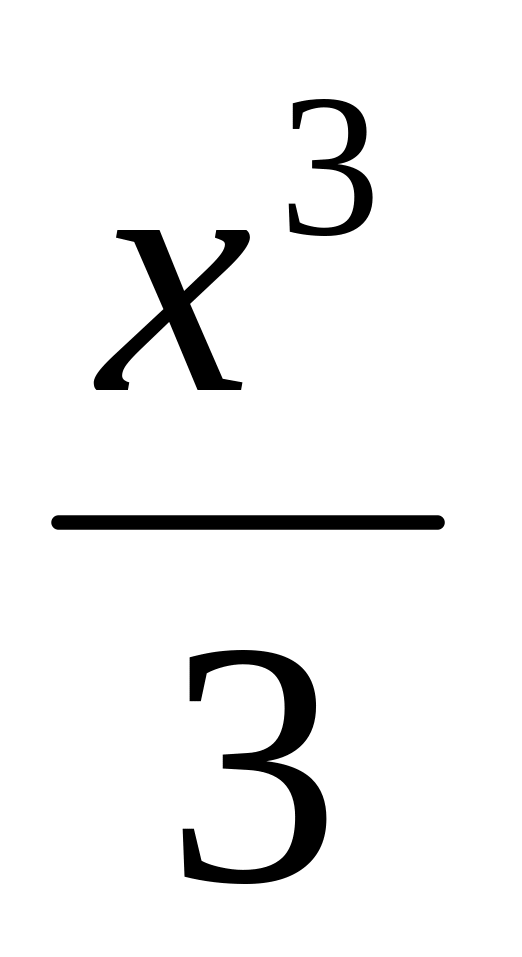 +
C;
+
C;y = x3 + C;
y = 3x3 + C;
y = 2x + C.
12. Дано
дифференциальное уравнение
![]() .
Найдите соотвествующее ему характерестическое
уравнение.
.
Найдите соотвествующее ему характерестическое
уравнение.
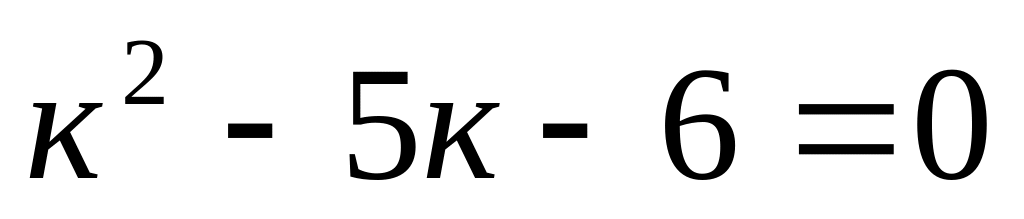 ;
;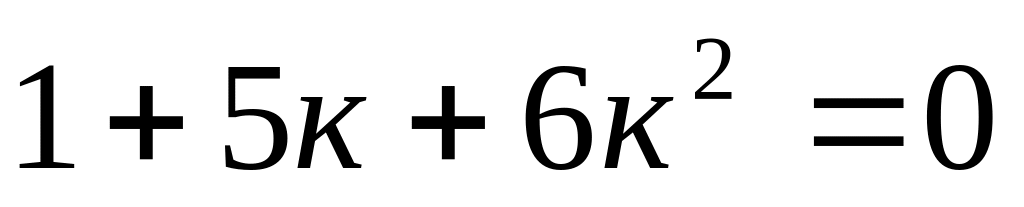 ;
;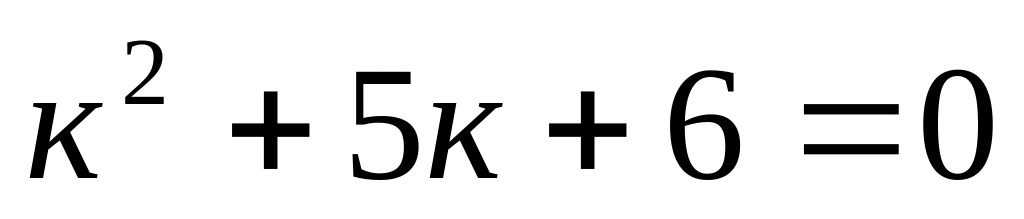 ;
;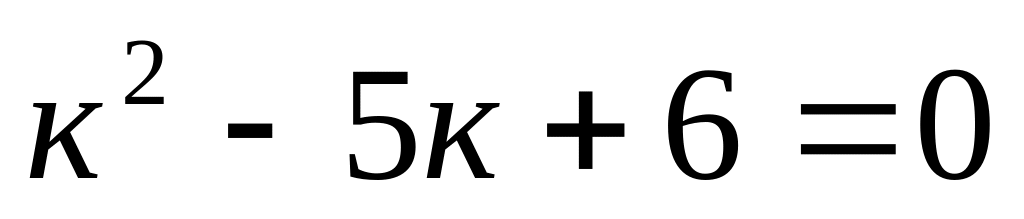 .
.
13. Укажите общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его характеристическое уравнение имеет вид у// – 4у/ = 0.
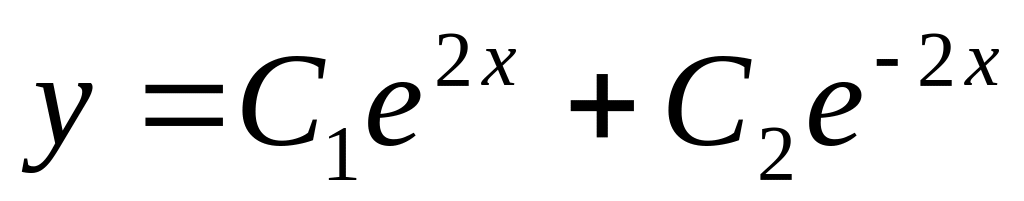 ;
;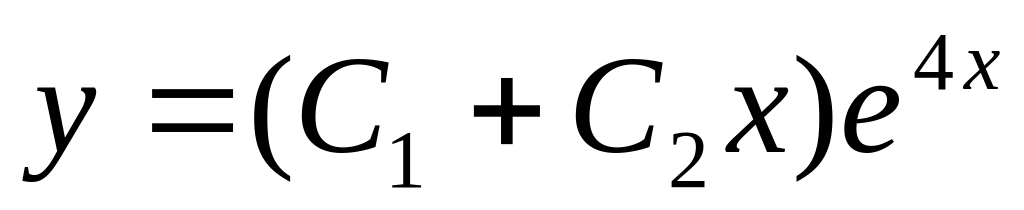 ;
;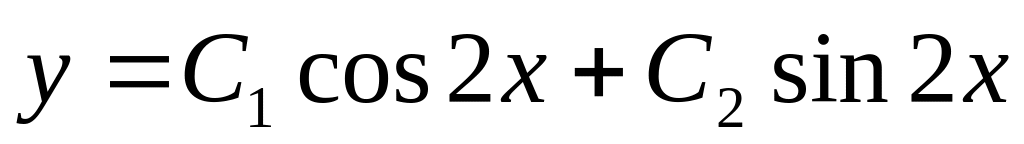 ;
;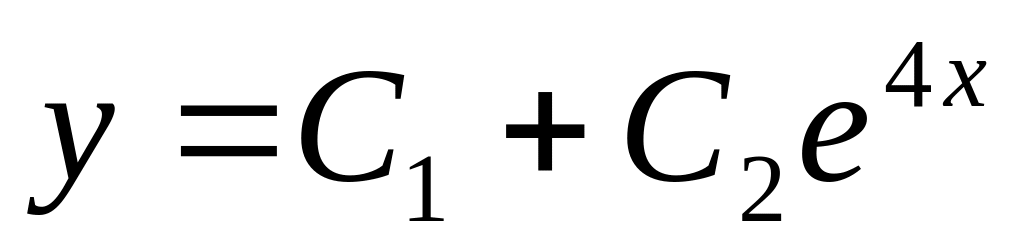 .
.
14. В каких пределах определяется вероятность случайного события Р(А)?
(– ∞; 0);
[1; + ∞);
[0; 1];
(– ∞; + ∞).
15. Среди 200 ламп 5 бракованных. Какова вероятность того, что взятая наугад лампа бракованная?
2,5%;
5%;
95%;
97,5%.
Ответы на задания В1, В2 и В3 запишите в указанном месте, а затем впишите в бланк тестирования справа от номера задания (В1, В2 или В3), начиная с первой клеточки.
В1. Найти
значение определенного интеграла
![]() .
.
Ответ______________________________ (1)
В2. Сколько различных трёхзначных чисел можно составить из цифр 0, 1, 2 так, чтобы в каждом числе не было одинаковых цифр
Ответ______________________________ (6)
В3. Найти наибольшее значение функции у = х2 – 4х + 6, если хϵ[0; 3]
Ответ______________________________ (6)
ОУ _________________________________________________________________________________
Курс _____ Группа ______________________ № (по списку)_________________________________
Математика Вариант 2
1. Что называется функцией?
Заданное число;
Правило, по которому каждому значению аргумента х в соответствует одно и только одно значение функции у;
Векторы, расположенные на параллельных прямых;
Определитель третьего порядка.
2. Последовательность задана формулой общего элемента хn= n3.Определите первые три члена этой последовательности:
0; 1; 3;
1; 4; 9;
2; 6; 8;
1; 8; 27.
3. Найти значение
предела
![]() .
.
3;
1;
0;
2.
4.
Чему равно значение предела
![]() ?
?
0;
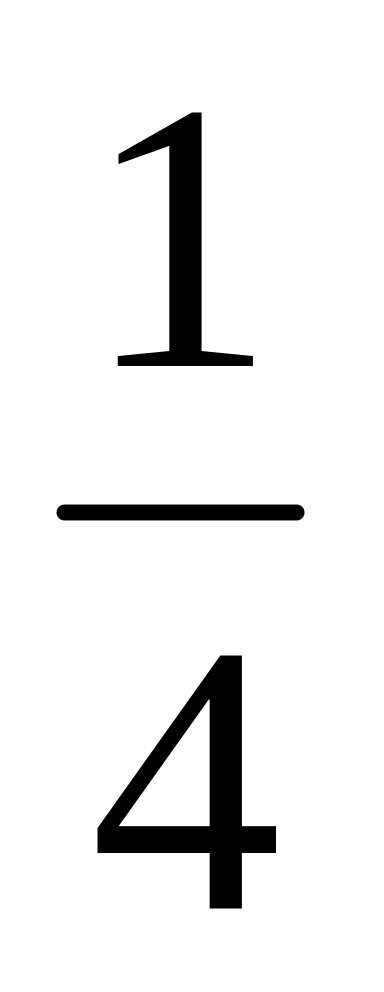 ;
;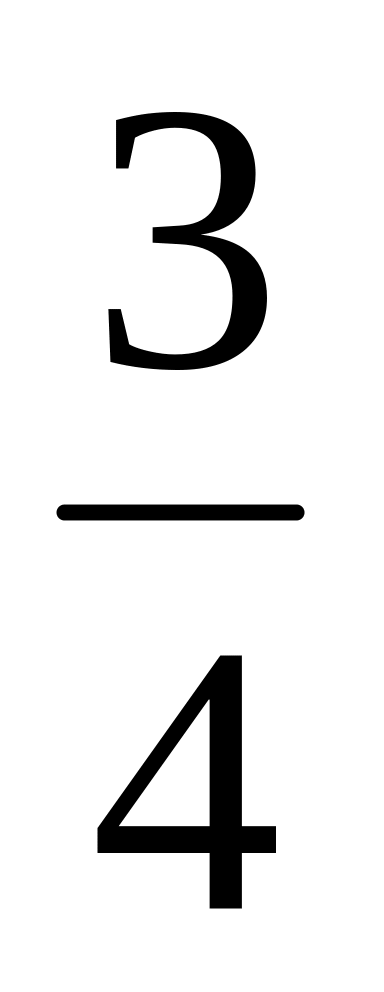 ;
;1.
5. Найти
значение прдела
![]() .
.
∞;
0;
2;
3.
6. Найти производную функции у = (2 – 5х)10.
у' = –20(2 – 5х)9;
у' = 10(2 – 5х)9;
у' = – 50х(2 – 5х)9;
у' = –50(2 – 5х)9.
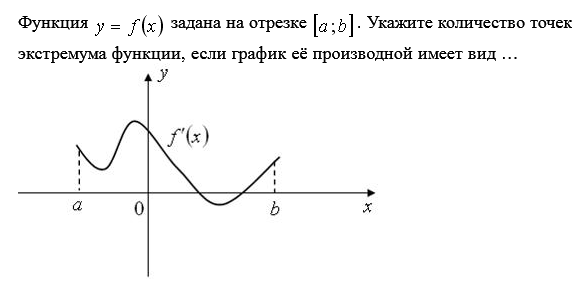
7. Чему равна
производная частного
![]() ?
?
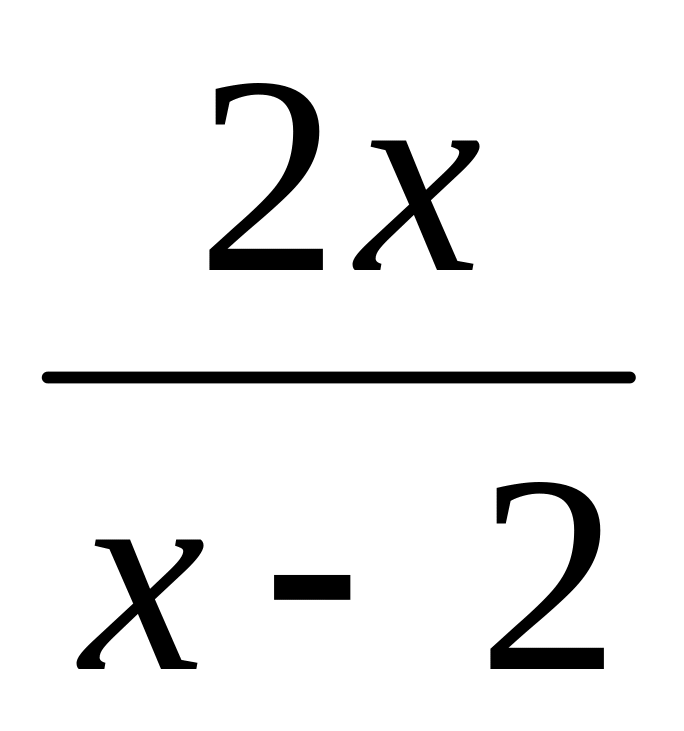 ;
;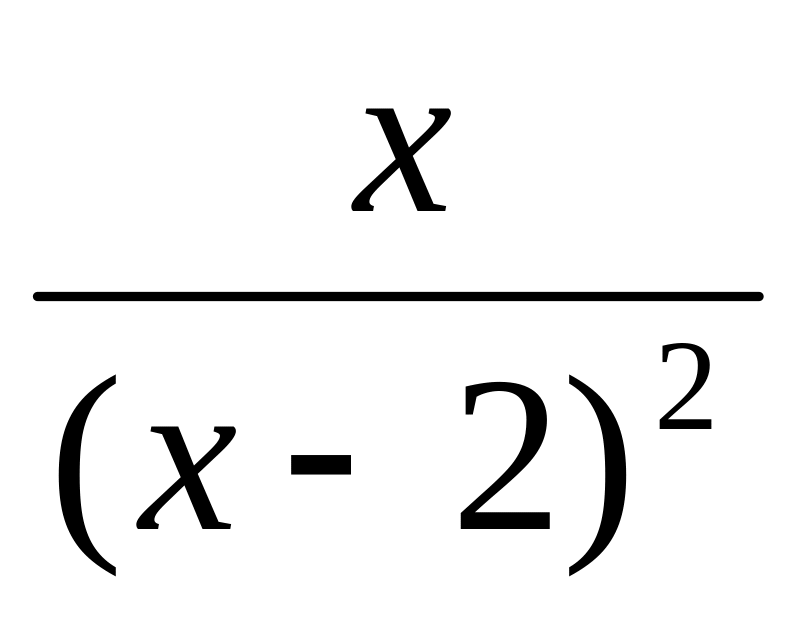 ;
;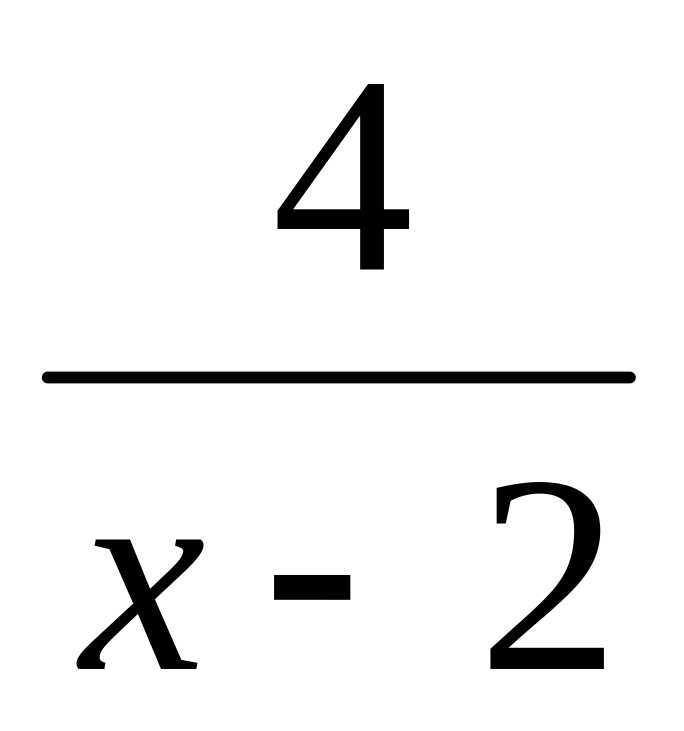 ;
;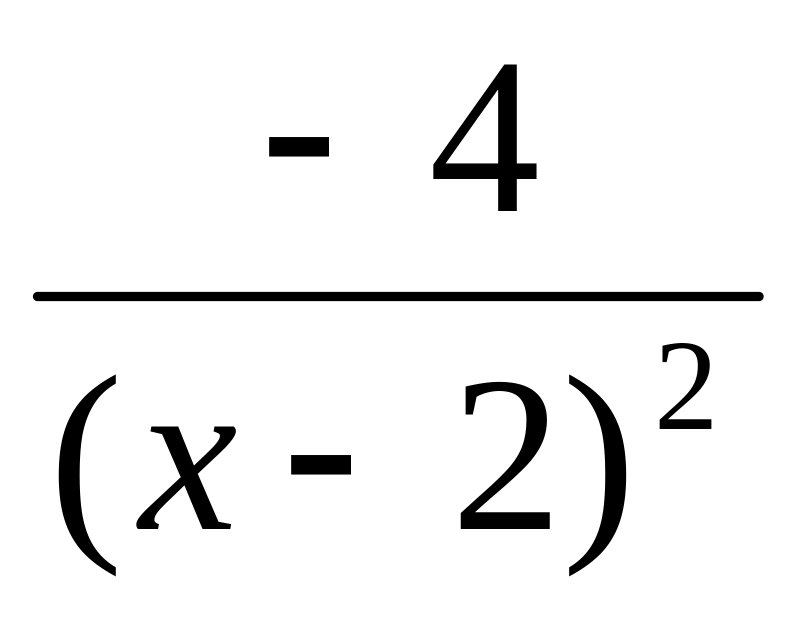
 .
.
8. На рисунке представлена функция y = f(x), заданная на отрезке [a; b]. Сколько точек экстремума имеет функция?
1;
2;
3;
4.
9.
Вычислить неопределенный интеграл
![]()
– ln|cosx| + C;
– ln|sinx| + C;
tgx +C;
ctgx + C.
10. Чем определяется порядок дифференциального уравнения?
Количеством операций (шагов) при его решении;
Количеством переменных величин в правой части;
Максимальной степенью переменной х;
Высшим порядком производной, входящей в уравнение.
11. Какое решение имеет дифференциальное уравнение первого порядка с разделяющимися переменными хdy = уdx?
у = 0,5х2 + С;
у = х∙С;
у = ех +С;
lnу = х + 2С.
12. Дано
дифференциальное уравнение
![]() .
Найдите соотвествующее ему характерестическое
уравнение.
.
Найдите соотвествующее ему характерестическое
уравнение.
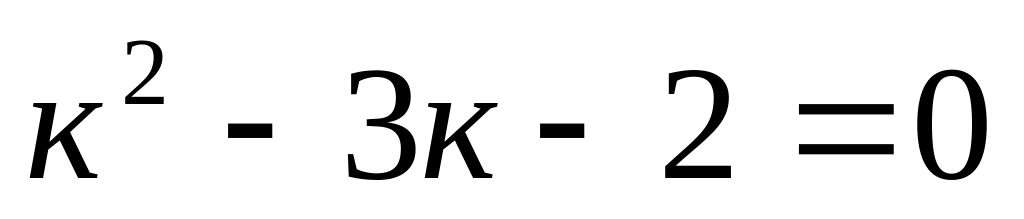 ;
; ;
;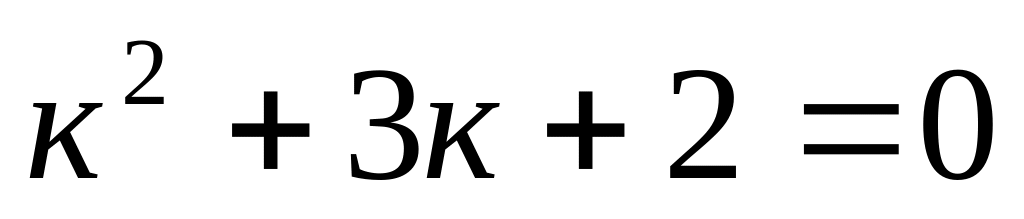 ;
;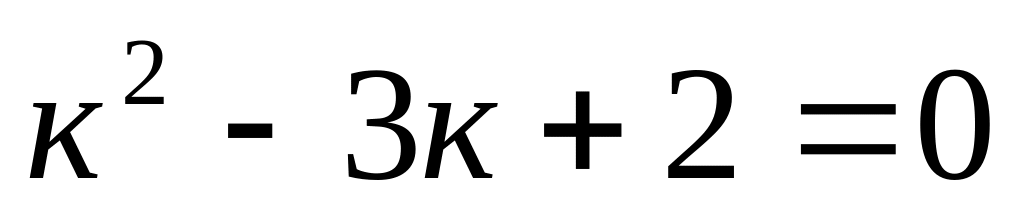 .
.
13. Укажите общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, если его характеристическое уравнение к2 – 4?
;
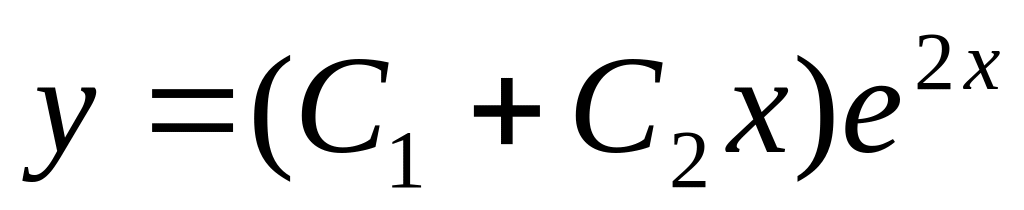 ;
;;
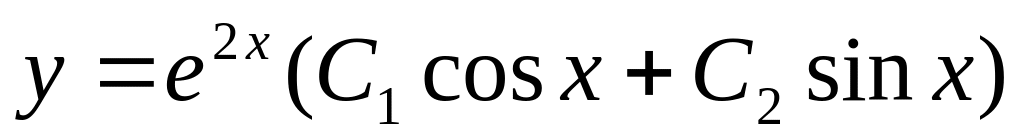 .
.
14. Чему равна вероятность невозможного события?
любому значению из промежутка [0; 1];
0,5;
0;
1.
15. Брошена наугад игральная кость. Какова вероятность того, что выпадет нечетное число очков?
25%;
30%;
50%;
75%.
Ответы на задания В1, В2 и В3 запишите в указанном месте, а затем впишите в бланк тестирования справа от номера задания (В1, В2 или В3), начиная с первой клеточки.
В1. Найти
значение определенного интеграла
![]() .
.
Ответ______________________________ (27)
В2. Энциклопедия состоит из пяти томов – с первого по пятый. Сколькими способами её можно поставить на полке?
Ответ______________________________ (120)
В3. Найти наибольшее значение функции у = 2х – х2 + 2, если хϵ[0; 3]
Ответ______________________________ (3)
ОУ _________________________________________________________________________________
Курс _____ Группа ______________________ № (по списку)_________________________________
