
- •Введение
- •1. Вычисление функций
- •Пояснения к программе
- •Пояснения к программе
- •2. Одномерные массивы
- •3. Матрицы
- •Пояснения к программе
- •Var а : Array [1..N, 1..N] of Real;
- •4. Обработка текстов
- •Пояснения к программе
- •Пояснения к программе
- •5. Процедуры и функции
- •Пояснения к программе
- •Пояснения к программе
- •Пояснения к программе
- •6. Перечисляемый и диапазонный типы
- •Пояснения к программе
- •7. Записи
- •8. Множества
- •9. Файлы
- •10. Списки
- •Пояснения к программе
- •Пояснения к программе
- •Библиографический список
- •Приложения
- •Комбинации клавиш управления в среде Turbo Pascal
- •Сообщения об ошибках периода компиляции
- •Оглавление
Пояснения к программе
Критерием окончания вычислений является заданная точность вычислений, поэтому число повторений цикла заранее неизвестно, процесс является итерационным и выход из цикла организуется по условию достижения требуемой точности. Вычислять каждый раз независимо степень xk и значение факториала k! нерационально, поэтому подсчет очередного члена ряда осуществляется через предыдущее значение по формуле
rk = rk-1 x / k .
program Iterative (input, output);
{ вычисление функции с помощью степенного ряда }
Var
Eps : Real; { точность вычислений }
X : Real; { аргумент }
R : Real; { очередной член ряда }
V : Real; { значение степенного ряда }
k : Integer; { счетчик членов ряда }
Begin
Writeln ('Введите точность вычислении');
Readln (Eps);
Writeln ('Введите аргумент');
Readln (X);
{ задание начального значения переменных цикла }
k := 1;
Y := 1;
R := X;
while abs(R) > Eps do
Begin
У := У + R;
k := k + 1;
R := R * X / k
End;
Writeln (' X =',Х:5:2,' ':5,'У = ', У + R:8:3)
End.
1.31. Составить программу для вычисления значения функции y = e-x с помощью разложения функции в степенной ряд (см. п. 1.30):
e-x = 1 – x/1! + x2/2! – x3/3! + … + (–1)n xn/n! + … .
1.32. Составить программу для вычисления значения функции y = sin(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
sin(x) = x – x3/3! + x5/5! – x7/7! + … + (-1)n x2n+1/(2n+1)! + … .
1.33. Составить программу для вычисления значения функции y = cos (x) с помощью разложения функции в степенной ряд (см. п. 1.30):
cos(x) = 1 – x2/2! + x4/4! – x6/6! + … + (–1)n x2n/(2n)! + … .
1.34. Составить программу для вычисления значения функции y = sh(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
sh(x) = x + x3/3! + x5/5! + x7/7! + … + x2n+1/(2n+1)! + … .
1.35. Составить программу для вычисления значения функции y = ch(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
ch(x) = 1 + x2/2! + x4/4! + x6/6! + … + x2n/(2n)! + … .
1.36. Составить программу для вычисления значения функции y = ln(1+x) с помощью разложения функции в степенной ряд (см. п. 1.30):
ln(1+x) = x/1 – x2/2 + x3/3 - x4/4 +… + (–1)n+1 xn/n + … .
1.37. Составить программу для вычисления значения функции y = ln(1-x) с помощью разложения функции в степенной ряд (см. п. 1.30):
ln(1-x) = – x/1 – x2/2 – x3/3 – x4/4–… – xn/n + … .
1.38. Составить
программу для вычисления значения
функции
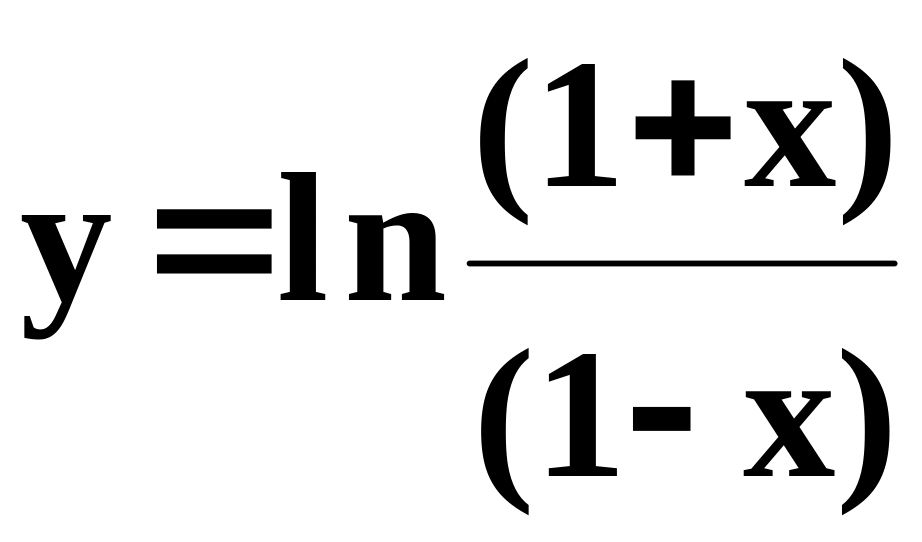 с помощью разложения функции в степенной
ряд (см. п. 1.30):
с помощью разложения функции в степенной
ряд (см. п. 1.30):
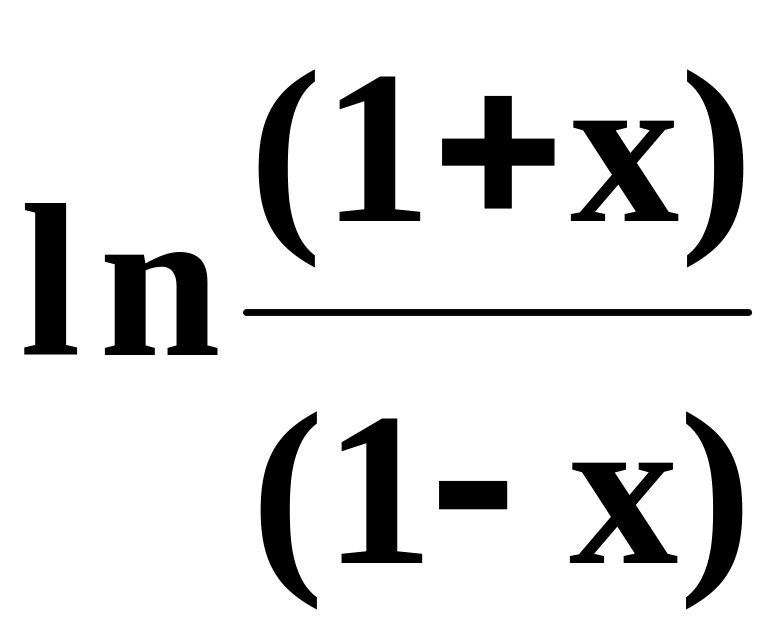 =
2( x/1
+ x3/3
+ x5/5
+ x7/7
+… + x2n+1/(2n+1)
+ …) .
=
2( x/1
+ x3/3
+ x5/5
+ x7/7
+… + x2n+1/(2n+1)
+ …) .
1.39. Составить программу для вычисления значения функции y =1/(1+x) с помощью разложения функции в степенной ряд (см. п. 1.30):
1/(1+x) = 1 – x + x2 – x3 + x4 -… + (–1)n xn + … .
1.40. Составить программу для вычисления значения функции y = 1/(1+x)2 с помощью разложения функции в степенной ряд (см. п. 1.30):
1/(1+x)2 = 1 – 2x + 3x2 – 4x3 + 5x4–… + (–1)n (n+1)xn + … .
1.41. Составить программу для вычисления значения функции y = 1/(1+x)3 с помощью разложения функции в степенной ряд (см. п. 1.30):
1/(1+x)3
= 1 –
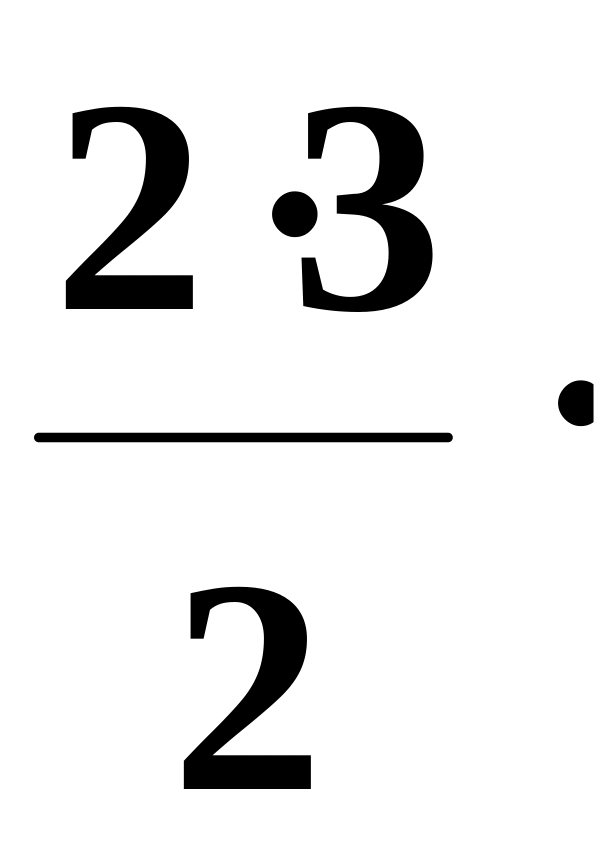 x
+
x
+
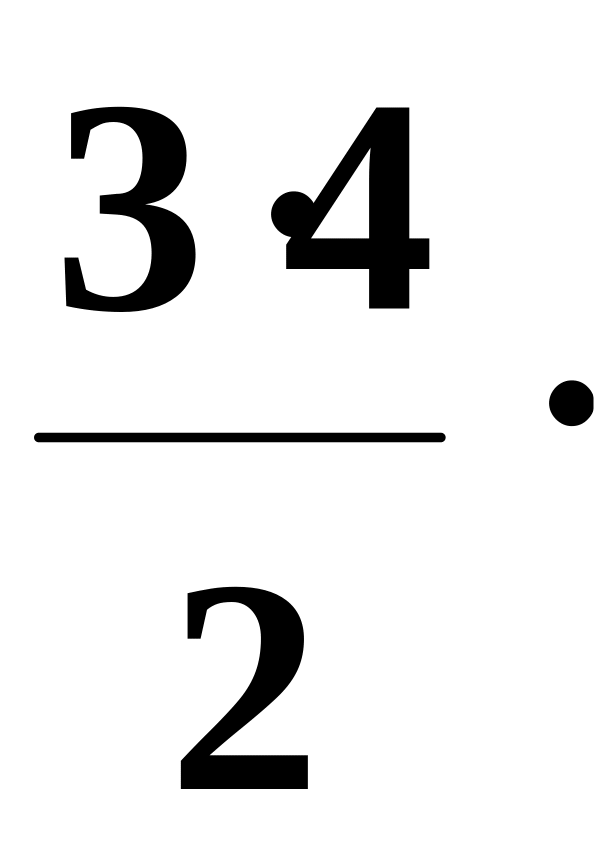 x2
–
x2
–
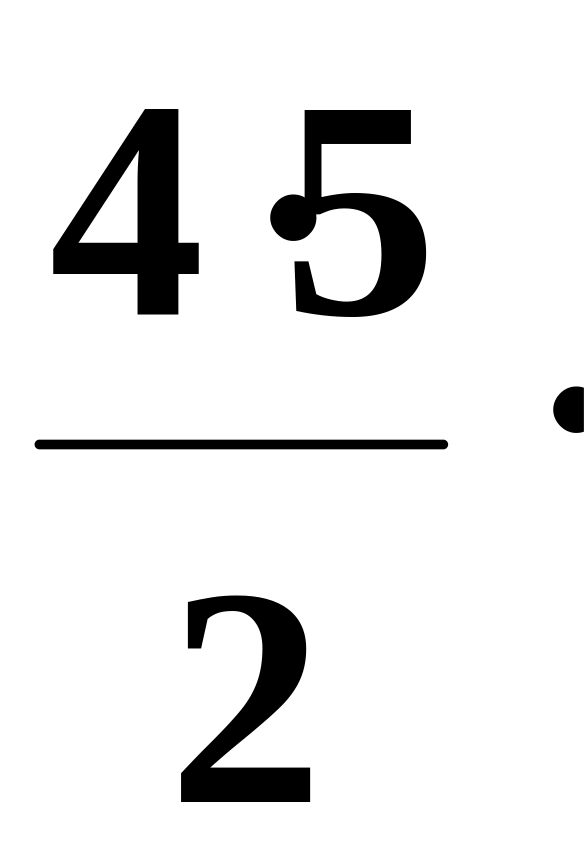 x3
+
…
+
x3
+
…
+
 xn
+….
xn
+….
1.42. Составить
программу для вычисления значения
функции
![]() с
помощью разложения функции в степенной
ряд (см. п. 1.30):
с
помощью разложения функции в степенной
ряд (см. п. 1.30):
![]() =
1 +
=
1 +
![]() x
–
x
–
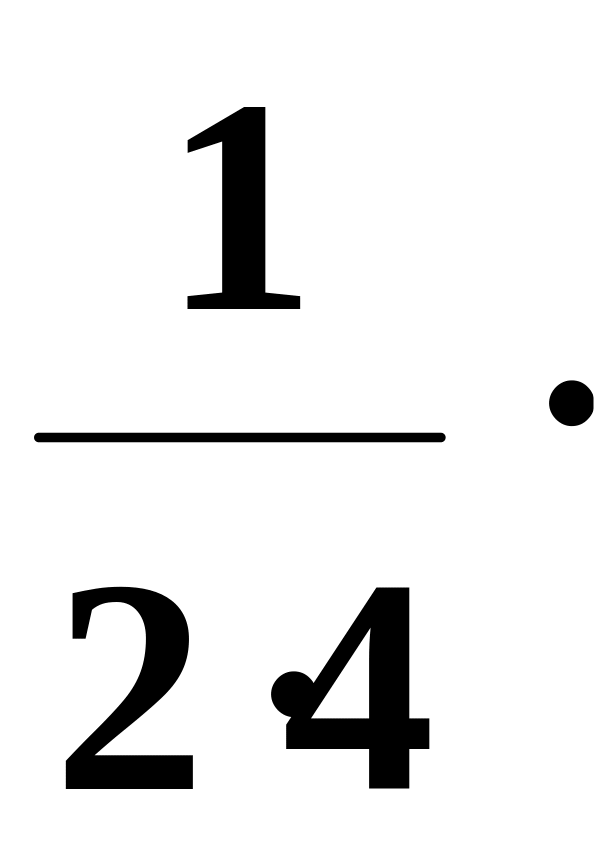 x2
+
x2
+
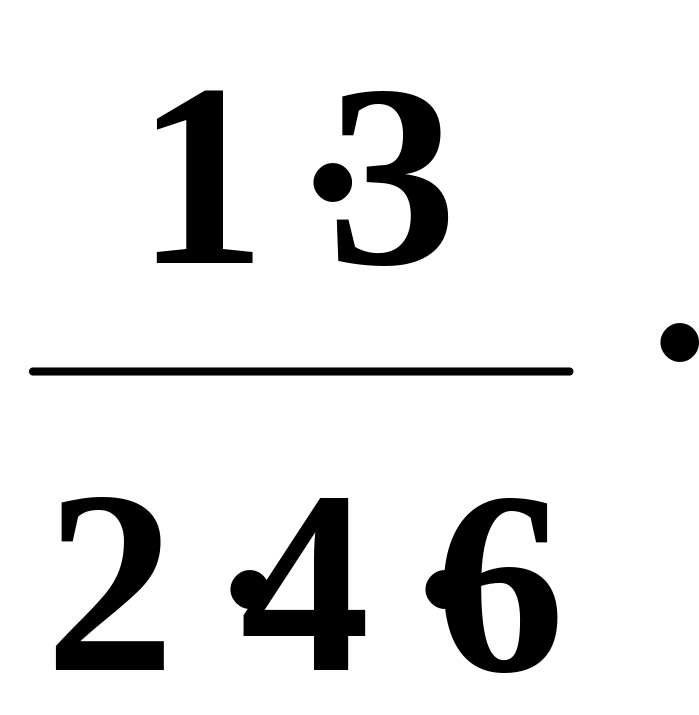 x3
– …
.
x3
– …
.
1.43. Составить
программу для вычисления значения
функции
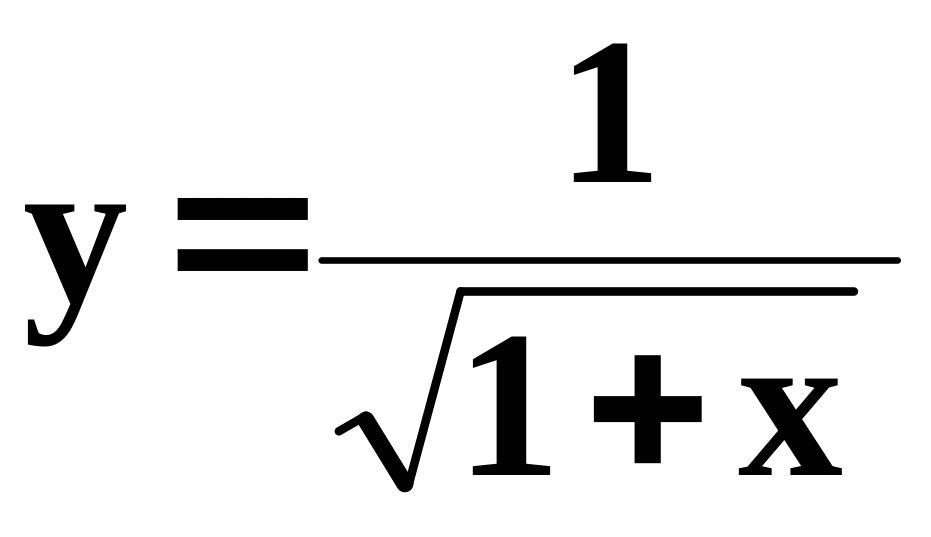 с
помощью разложения функции в степенной
ряд (см. п. 1.30):
с
помощью разложения функции в степенной
ряд (см. п. 1.30):
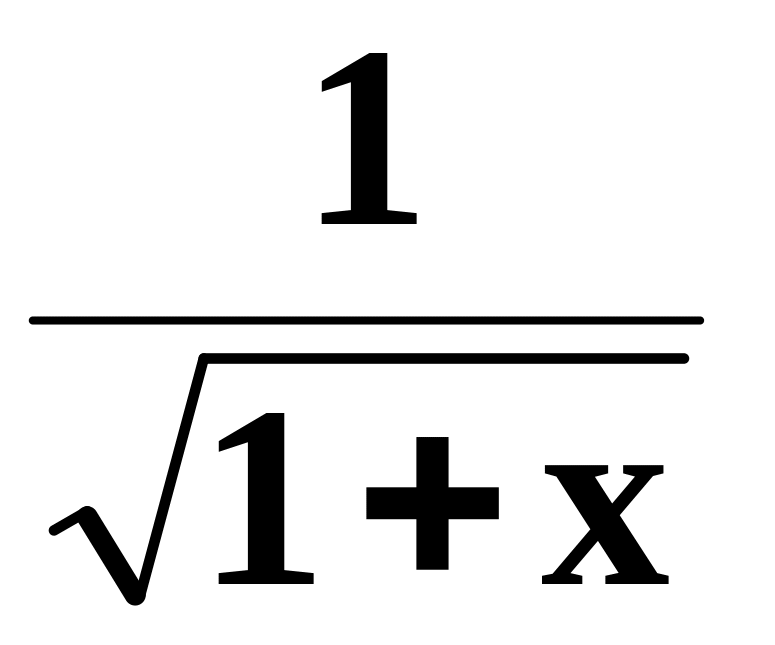 =
1
–
x
+
=
1
–
x
+
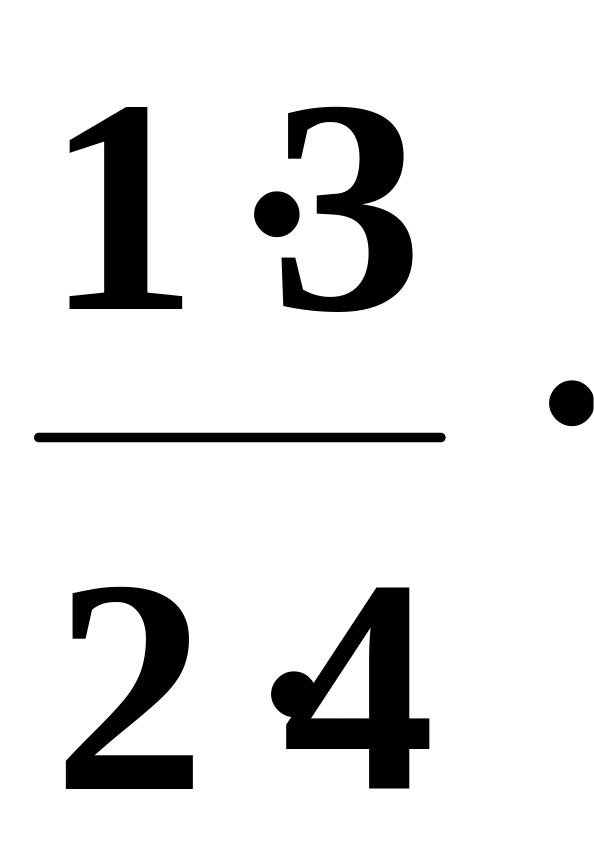 x2
–
x2
–
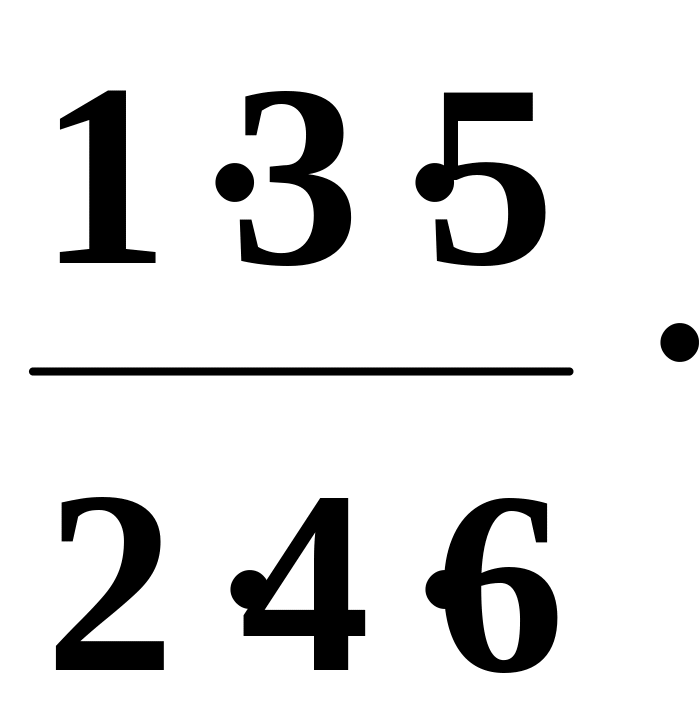 x3
+ … .
x3
+ … .
1.44. Составить
программу для вычисления значения
функции
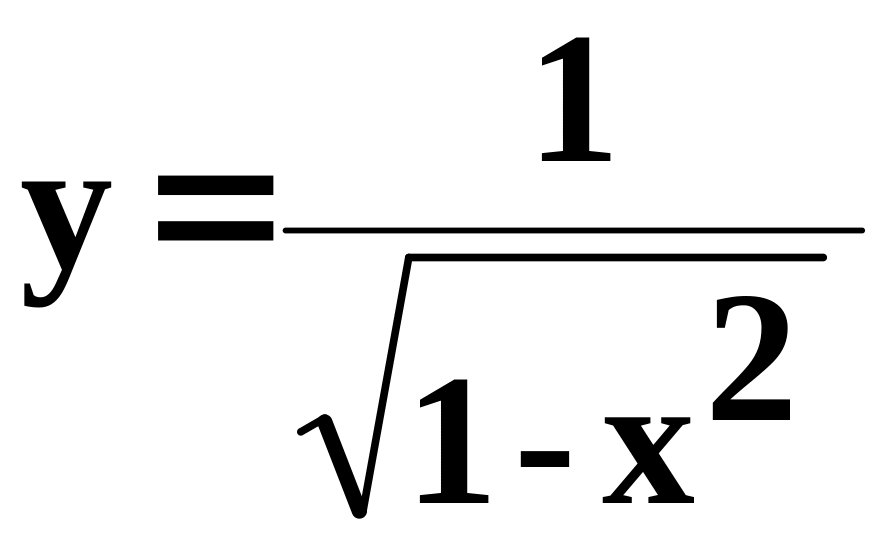 с
помощью разложения функции в степенной
ряд (см. п. 1.30):
с
помощью разложения функции в степенной
ряд (см. п. 1.30):
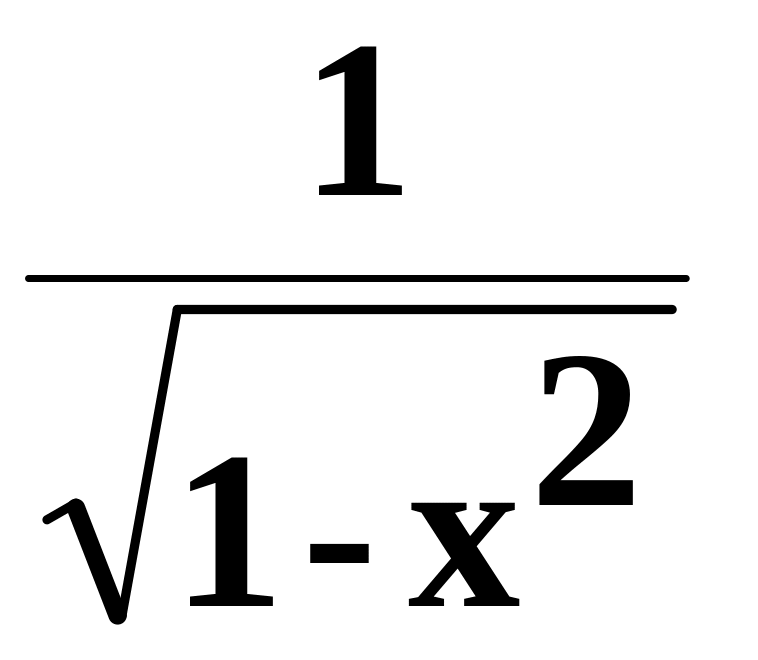 =
1
+
x2
+
x4
+
x6
+ … .
=
1
+
x2
+
x4
+
x6
+ … .
1.45. Составить
программу для вычисления значения
функции
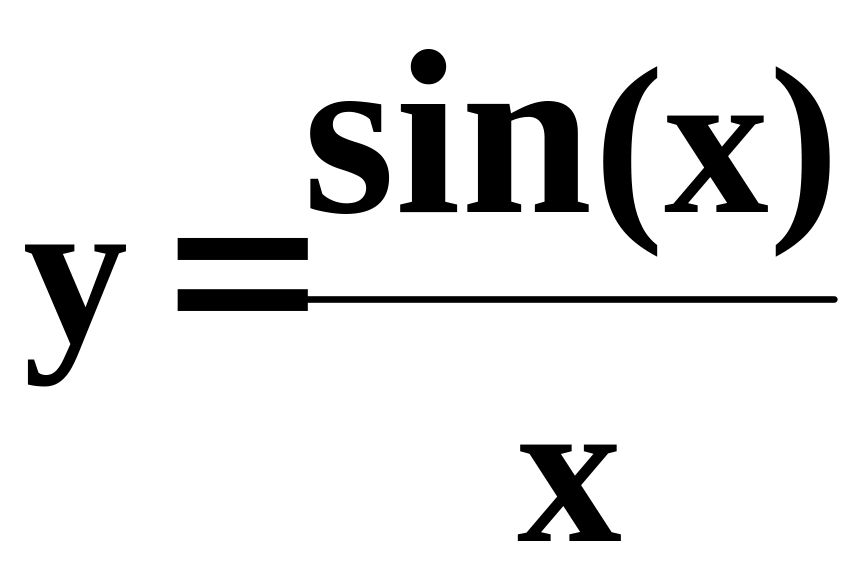 с помощью разложения функции в степенной
ряд (см. п. 1.30):
с помощью разложения функции в степенной
ряд (см. п. 1.30):
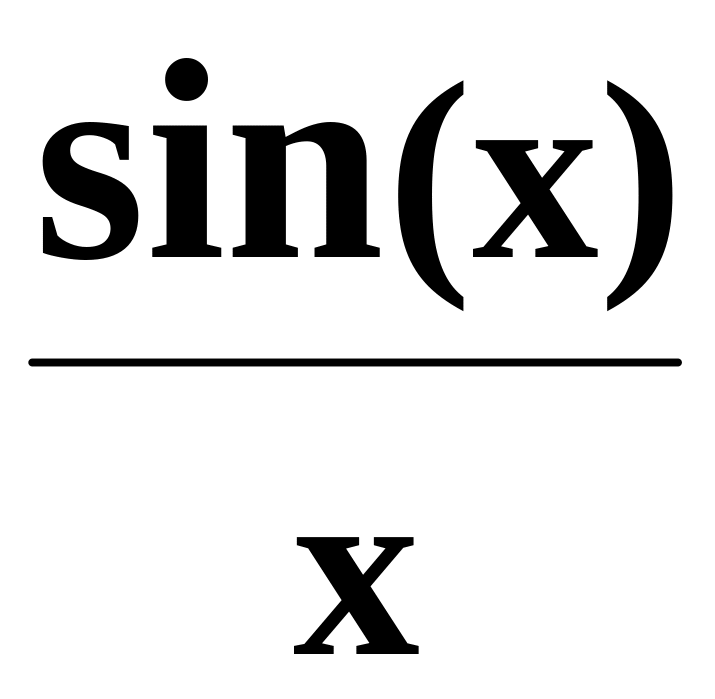 =
1
– x2/3!
+ x4/5!
– x6/7!
+ … + (–1)n
x2n/(2n+1)!
+ … .
=
1
– x2/3!
+ x4/5!
– x6/7!
+ … + (–1)n
x2n/(2n+1)!
+ … .
1.46. Составить
программу для вычисления значения
функции
![]() с помощью разложения функции в степенной
ряд (см. п. 1.30):
с помощью разложения функции в степенной
ряд (см. п. 1.30):
![]() =
1
– x2/1!
+ x4/2!
– x6/3!
+ … + (–1)n
x2n/n!
+ … .
=
1
– x2/1!
+ x4/2!
– x6/3!
+ … + (–1)n
x2n/n!
+ … .
1.47. Составить программу для вычисления значения функции y = arctg(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
arctg(x) = x – x3/3 + x5/5 – x7/7 + … + (–1)n x2n+1/(2n+1) + … .
1.48. Составить программу для вычисления значения функции y = arcsin(x) с помощью разложения функции в степенной ряд (см. п. 1.30):
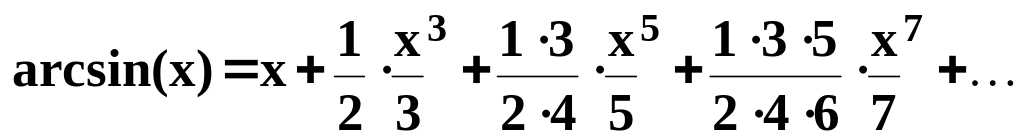
1.49. Составить
программу для вычисления функции y
=
![]() с
помощью разложения функции в степенной
ряд (см. п. 1.30):
с
помощью разложения функции в степенной
ряд (см. п. 1.30):

